Chủ đề Hằng đẳng thức 9: Hằng đẳng thức 9 trong toán học là tổng hai lập phương, được coi là một trong những hằng đẳng thức đáng nhớ và quan trọng. Nó cho phép chúng ta tính toán tổng hai lập phương một cách dễ dàng và chính xác. Việc biết và áp dụng hằng đẳng thức này sẽ giúp chúng ta giải quyết một số bài toán liên quan đến lập phương một cách hiệu quả.
Hằng đẳng thức nào liên quan đến căn bậc hai trong toán lớp 9?
Hằng đẳng thức liên quan đến căn bậc hai trong toán lớp 9 bao gồm:
1. Bình phương của một tổng (a + b)2 = a2 + 2ab + b2.
Đây là hằng đẳng thức biểu diễn cách tính bình phương của một tổng hai số. Ta chỉ cần nhân hai số đầu tiên lại với nhau, rồi nhân với hai, cuối cùng thêm bình phương của số thứ hai vào.
2. Bình phương của một hiệu (a - b)2 = a2 - 2ab + b2.
Hằng đẳng thức này biểu diễn cách tính bình phương của một hiệu hai số. Ta nhân hai số đầu tiên lại với nhau, rồi nhân với âm hai, cuối cùng thêm bình phương của số thứ hai vào.
3. Tổng hai lập phương a3 + b3 = (a + b)(a2 - ab + b2).
Hằng đẳng thức này biểu diễn cách tính tổng hai lập phương. Ta có thể nhân hai số lại với nhau, rồi áp dụng hằng đẳng thức bình phương của một hiệu để biểu diễn tổng hai lập phương.
Đây chỉ là một số hằng đẳng thức liên quan đến căn bậc hai trong toán lớp 9. Còn nhiều hằng đẳng thức nữa mà bạn có thể tìm hiểu thêm.
Hằng đẳng thức căn bậc hai nào là những hằng đẳng thức quan trọng cần biết trong toán lớp 9?
Hằng đẳng thức căn bậc hai quan trọng cần biết trong toán lớp 9 bao gồm:
1. Hằng đẳng thức căn bậc hai của tổng: (√a + √b)² = a + 2√ab + b
Đây là một hằng đẳng thức quan trọng khi cần tính căn bậc hai của tổng hai số hạng.
2. Hằng đẳng thức căn bậc hai của hiệu: (√a - √b)² = a - 2√ab + b
Đây là một hằng đẳng thức quan trọng khi cần tính căn bậc hai của hiệu hai số hạng.
3. Hằng đẳng thức căn bậc hai của tích: (√a * √b)² = ab
Đây là một hằng đẳng thức quan trọng khi cần tính căn bậc hai của tích hai số hạng.
4. Hằng đẳng thức căn bậc hai của thương: (√a / √b)² = a/b
Đây là một hằng đẳng thức quan trọng khi cần tính căn bậc hai của thương hai số hạng.
5. Hằng đẳng thức căn bậc hai của nghịch đảo: (√a)² = a
Đây là một hằng đẳng thức quan trọng khi cần tìm căn bậc hai của số hạng bình phương.
Những hằng đẳng thức này giúp chúng ta rút gọn biểu thức, tính toán các phép toán căn bậc hai, và áp dụng vào các bài toán thực tế. Qua việc nắm vững hằng đẳng thức này, học sinh lớp 9 sẽ có thể giải các bài toán liên quan đến căn bậc hai một cách hiệu quả.
Hãy liệt kê 7 hằng đẳng thức đáng nhớ liên quan đến bình phương của tổng và hiệu của hai số?
Dưới đây là danh sách 7 hằng đẳng thức đáng nhớ liên quan đến bình phương của tổng và hiệu của hai số:
1. Bình phương của một tổng (a + b)^2 = a^2 + 2ab + b^2: Khi ta nhân đôi một tổng, ta sẽ nhận được tổng của bình phương hai số ban đầu và gấp đôi tích của hai số đó.
2. Bình phương của một hiệu (a - b)^2 = a^2 - 2ab + b^2: Tương tự như trên, khi ta nhân đôi một hiệu, ta sẽ nhận được tổng của bình phương hai số ban đầu và gấp đôi tích của hai số đó.
3. Công thức tổng của bình phương (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc: Công thức này cho biết rằng bình phương của một tổng ba số bằng tổng của các bình phương của từng số và gấp đôi tích của các cặp số.
4. Công thức hiệu của bình phương (a - b)^2 = a^2 + b^2 - 2ab: Tương tự như trên, công thức này cho biết rằng bình phương của một hiệu hai số bằng tổng của các bình phương của từng số và gấp đôi tích của hai số đó với nhau.
5. Công thức bình phương của một tổng và một hiệu (a + b)(a - b) = a^2 - b^2: Công thức này biểu thị rằng tích của một tổng và một hiệu bằng hiệu của các bình phương của từng số.
6. Công thức tổng các bình phương (a^2 + b^2) = (a + b)^2 - 2ab: Công thức này cho biết rằng tổng của các bình phương của hai số bằng bình phương của tổng hai số đó trừ đi gấp đôi tích của hai số đó với nhau.
7. Công thức hiệu các bình phương (a^2 - b^2) = (a + b)(a - b): Công thức này cho biết rằng hiệu của các bình phương của hai số bằng tích của tổng và hiệu của hai số đó.
Hằng đẳng thức nào sử dụng để tính tổng hai lập phương?
Hằng đẳng thức sử dụng để tính tổng hai lập phương là hằng đẳng thức căn bậc hai. Theo hằng đẳng thức căn bậc hai, ta có công thức tính tổng hai lập phương như sau:
(a + b)^2 = a^2 + 2ab + b^2
Trong đó, a và b là hai số thực bất kỳ. Để tính tổng hai lập phương, ta chỉ cần áp dụng công thức trên với a và b là hai số lập phương cần tính tổng. Kết quả của phép tính trên chính là tổng của hai lập phương đó.
Ví dụ: Để tính tổng hai số lập phương 4 và 3, ta thực hiện như sau:
(4 + 3)^2 = 4^2 + 2*4*3 + 3^2 = 49
Vậy tổng hai lập phương 4 và 3 là 49.
Toán lớp 9 - Bài 2: Căn thức bậc hai và hằng đẳng thức
Video hướng dẫn toán lớp 9 sẽ giúp bạn nắm vững kiến thức và giải quyết công việc toán hàng ngày một cách dễ dàng. Hãy xem ngay để trở thành người giỏi toán trong lớp của bạn!
Cách sử dụng hằng đẳng thức bình phương của một tổng (a + b)^2 = a^2 + 2ab + b^2 trong giải toán?
Cách sử dụng hằng đẳng thức bình phương của một tổng (a + b)^2 = a^2 + 2ab + b^2 trong giải toán như sau:
Bước 1: Xác định các giá trị của a và b trong bài toán.
Bước 2: Áp dụng hằng đẳng thức (a + b)^2 = a^2 + 2ab + b^2 để thay thế cho biểu thức bên trái của phương trình bài toán.
Bước 3: Tính toán các phép tính trong biểu thức bên phải của hằng đẳng thức.
Bước 4: Giải quyết phương trình và tìm ra giá trị của a và b dựa trên biểu thức đã được tính toán ở bước trước.
Bước 5: Kiểm tra lại kết quả và đưa ra câu trả lời cuối cùng.
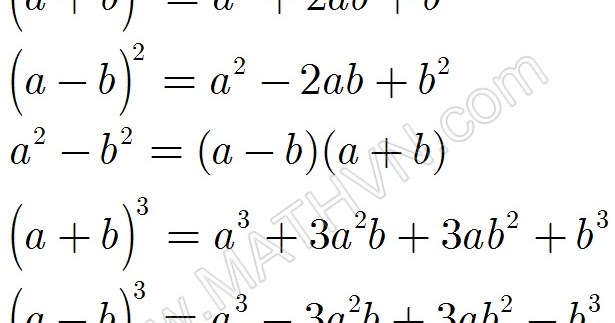
_HOOK_
Hằng đẳng thức bình phương của một hiệu (a - b)^2 = a^2 - 2ab + b^2 được áp dụng như thế nào trong các bài toán toán học?
Hằng đẳng thức bình phương của một hiệu (a - b)^2 = a^2 - 2ab + b^2 là một trong 7 hằng đẳng thức đáng nhớ trong toán học. Đây là một công thức quan trọng với nhiều ứng dụng trong giải các bài toán toán học.
Để áp dụng hằng đẳng thức này vào giải các bài toán, ta cần hiểu rõ ý nghĩa và cách sử dụng của nó. Công thức này cho phép chúng ta biến đổi một hiệu số thành một tổng các bình phương và các tích hai số. Cụ thể, đối với một phép trừ (a - b), ta có thể tính bình phương của hiệu đó bằng cách nhân toán tử (a - b) với chính nó.
Ví dụ: Giả sử ta có một bài toán yêu cầu tính giá trị của biểu thức (5 - 3)^2. Ta áp dụng hằng đẳng thức trên, ta có:
(5 - 3)^2 = 5^2 - 2(5)(3) + 3^2 = 25 - 30 + 9 = 4
Bài toán này đã được giải bằng cách sử dụng hằng đẳng thức bình phương của một hiệu (a - b)^2 = a^2 - 2ab + b^2. Ta thực hiện các phép tính để biến đổi biểu thức cho đúng và tìm giá trị kết quả.
Hằng đẳng thức này còn được sử dụng trong các bài toán liên quan đến tính diện tích, thể tích, và trong quá trình chứng minh những phép biến đổi công thức. Nó giúp chúng ta rút gọn biểu thức, tạo thuận lợi trong quá trình tính toán và chứng minh.
Tóm lại, hằng đẳng thức bình phương của một hiệu (a - b)^2 = a^2 - 2ab + b^2 là một công thức quan trọng và rất hữu ích trong giải các bài toán toán học, giúp chúng ta thực hiện các phép biến đổi và tính toán một cách thuận lợi và chính xác.
Đặt ví dụ cụ thể về việc áp dụng hằng đẳng thức trong việc tính toán và giải bài toán.
Để áp dụng hằng đẳng thức trong việc tính toán và giải bài toán, chúng ta có thể đặt ví dụ cụ thể như sau:
Ví dụ 1: Giải phương trình bậc hai bằng cách sử dụng hằng đẳng thức căn bậc hai.
Cho phương trình: x^2 - 4x + 4 = 0. Ta có thể nhận thấy rằng phương trình này có dạng (a - b)^2 = 0, tương đương với hằng đẳng thức (x - 2)^2 = 0.
Áp dụng hằng đẳng thức căn bậc hai: nếu một biểu thức có dạng (ax + b)^2 = 0, thì ta có thể suy ra rằng ax + b = 0.
Áp dụng hằng đẳng thức vào ví dụ trên: (x - 2)^2 = 0, suy ra x - 2 = 0, từ đó ta có x = 2.
Vậy, nghiệm của phương trình là x = 2.
Ví dụ 2: Tính giá trị biểu thức sử dụng hằng đẳng thức tổng hai lập phương.
Cho biểu thức: A = (a + b)^3 - (a - b)^3. Ta hãy tính giá trị của A.
Áp dụng hằng đẳng thức tổng hai lập phương: (a + b)^3 - (a - b)^3 = 3a^2b + 3ab^2.
Áp dụng hằng đẳng thức vào ví dụ trên: A = 3a^2b + 3ab^2.
Như vậy, giá trị của biểu thức A là 3a^2b + 3ab^2.
Hy vọng những ví dụ trên đã giúp bạn hiểu rõ hơn về cách áp dụng hằng đẳng thức trong việc tính toán và giải bài toán.

Toán lớp 9 - Bài 2: Căn bậc hai và hằng đẳng thức
Xem video về công thức căn bậc hai sẽ giúp bạn hiểu rõ hơn về cách tính căn của một số. Sự dễ dàng và linh hoạt của video sẽ khiến bạn trở nên thành thạo trong việc tính căn bậc hai!
Căn thức bậc hai và hằng đẳng thức - Bài 2 Toán lớp 9 - Cô Phạm Thị Huệ Chi (DỄ HIỂU NHẤT)
Đừng bỏ lỡ video hướng dẫn về hằng đẳng thức, nơi bạn sẽ được giải thích một cách chi tiết và dễ hiểu về các loại đẳng thức khác nhau. Xem ngay để nắm vững hằng đẳng thức và áp dụng vào bài tập!
Tại sao hằng đẳng thức là một khái niệm quan trọng trong toán học và được ứng dụng rộng rãi trong nhiều lĩnh vực?
Hằng đẳng thức là một khái niệm quan trọng trong toán học vì nó giúp chúng ta biểu diễn mối quan hệ toán học một cách chính xác và rõ ràng. Bằng cách sử dụng hằng đẳng thức, chúng ta có thể chứng minh và suy luận về các phương trình và bất đẳng thức mà không cần thực hiện các phép tính phức tạp.
Hằng đẳng thức cũng có thể được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Ví dụ, trong vật lý, hằng đẳng thức được sử dụng để mô tả các mối quan hệ giữa các đại lượng vật lý như áp suất, lực, công suất và nhiệt độ. Trong kỹ thuật, chúng ta có thể sử dụng hằng đẳng thức để thiết kế và phân tích các mạch điện, hệ thống điện tử và cơ cấu máy. Trong kinh tế học, hằng đẳng thức có thể được sử dụng để mô phỏng và dự đoán các mô hình kinh tế và tài chính.
Hằng đẳng thức còn đóng vai trò quan trọng trong quá trình giảng dạy và học tập. Việc hiểu và áp dụng hằng đẳng thức giúp chúng ta tăng cường khả năng tư duy logic và phản biện, đồng thời cũng giúp chúng ta phát triển kỹ năng giải quyết vấn đề và sáng tạo.
Tóm lại, hằng đẳng thức là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu và áp dụng hằng đẳng thức giúp chúng ta hiểu sâu hơn về mối quan hệ toán học và tăng cường khả năng trong việc giải quyết các vấn đề phức tạp.
Có những hằng đẳng thức nào khác liên quan đến căn bậc hai mà cần biết trong toán học?
Một số hằng đẳng thức khác liên quan đến căn bậc hai mà cần biết trong toán học bao gồm:
1. Căn bậc hai của một tích: √(a * b) = √a * √b
Đây là hằng đẳng thức cho phép chia căn bậc hai của một tích thành tích của căn bậc hai của từng nhân tử.
2. Căn bậc hai của một thương: √(a / b) = √a / √b
Tương tự như trường hợp trên, hằng đẳng thức này cho phép chia căn bậc hai của một thương thành thương của căn bậc hai của từng phần tử.
3. Căn bậc hai của một tổng: √(a + b) ≠ √a + √b
Khác với tích và thương, hằng đẳng thức này không thể phân tách căn bậc hai của một tổng thành tổng của căn bậc hai của từng phần tử.
4. Căn bậc hai của bình phương: √(a^2) = |a|
Hằng đẳng thức này chỉ ra rằng căn bậc hai của một số bình phương sẽ luôn là giá trị tuyệt đối của số đó.
Nhớ rằng các hằng đẳng thức này chỉ đúng cho các giá trị dương và phải tuân theo các điều kiện phù hợp.
Nêu một số ví dụ về các bài toán sử dụng hằng đẳng thức căn bậc hai trong cuộc sống hàng ngày.
Một vài ví dụ về các bài toán sử dụng hằng đẳng thức căn bậc hai trong cuộc sống hàng ngày như sau:
1. Diện tích hình chữ nhật: Diện tích của hình chữ nhật có thể tính bằng hằng đẳng thức căn bậc hai. Ví dụ, khi biết độ dài hai cạnh của hình chữ nhật, ta có thể dùng công thức S = √(a * b) để tính diện tích, trong đó a và b là các cạnh của hình chữ nhật.
2. Tính diện tích hình tam giác: Diện tích của hình tam giác có thể được tính bằng hằng đẳng thức căn bậc hai. Ví dụ, khi biết độ dài ba cạnh của hình tam giác, ta có thể dùng công thức Heron để tính diện tích, trong đó S = √(p * (p - a) * (p - b) * (p - c)), trong đó p là nửa chu vi của tam giác và a, b, c là các cạnh của tam giác.
3. Tính khoảng cách: Khi có hai điểm trong mặt phẳng, ta có thể tính khoảng cách giữa hai điểm đó bằng hằng đẳng thức căn bậc hai. Ví dụ, khi biết tọa độ (x1, y1) và (x2, y2) của hai điểm, ta có thể dùng công thức khoảng cách Euclid để tính khoảng cách, trong đó d = √((x2 - x1)^2 + (y2 - y1)^2).
4. Tính thời gian: Trong một số bài toán về thời gian, ta có thể sử dụng hằng đẳng thức căn bậc hai để tính toán. Ví dụ, khi biết vận tốc và khoảng cách, ta có thể dùng công thức thời gian = khoảng cách / vận tốc để tính thời gian.
Những ví dụ trên chỉ là một số bài toán sử dụng hằng đẳng thức căn bậc hai trong cuộc sống hàng ngày. Hằng đẳng thức căn bậc hai là một công cụ hữu ích trong việc giải các bài toán toán học và thường được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau.
_HOOK_