Cách chứng minh hình thang cân thông qua việc chứng minh hình thang có 2 góc kề một đáy bằng nhau, hai đường chéo bằng nhau hoặc hình thang nội tiếp đường tròn.

Bài viết này được đăng tại cuongthinhcorp.com.vn, không được copy dưới mọi hình thức.
Hình thang cân là một trường hợp đặc biệt của hình thang, và chứng minh hình thang cân là một phần bài tập quan trọng trong chương trình Hình học lớp 8, vậy các em đã nắm được các cách chứng minh hình thang cân chưa nào? Nếu chưa thì hãy cùng lướt ngay xuống bên dưới để freetuts hướng dẫn cho các em 3 cách chứng minh siêu chi tiết và dễ hiểu nha.
Tóm tắt lý thuyết hình thang cân
Trước khi đi tìm hiểu về cách chứng minh hình thang cân, hãy cùng ôn lại các định nghĩa, tính chất và dấu hiệu nhận biết hình thang ngay dưới đây nhé.
Định nghĩa hình thang cân trong toán học
Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau, đây là một trường hợp đặc biệt của hình thang.
Bài viết này được đăng tại [free tuts .net]
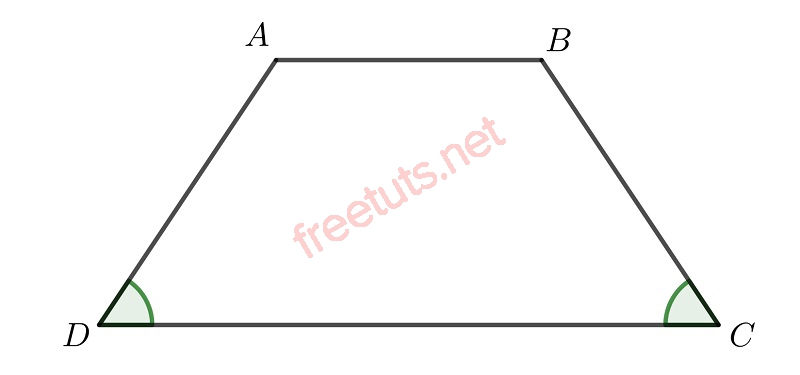
Hình ảnh hình thang cân ABCD.
Cho hình thang ABCD có 2 cạnh đáy là AB và DC, ABCD là hình thang cân khi và chỉ khi
AB // CD, góc A = góc B, góc C = góc D.
Tính chất, định lý hình thang cân
Trong một hình thang cân, ta có:
- Hai cạnh bên bằng nhau.
- Hai góc kề một cạnh đáy bằng nhau.
- Hai đường chéo bằng nhau
- Hai cạnh đáy song song với nhau
- Hình thang cân nội tiếp đường tròn.
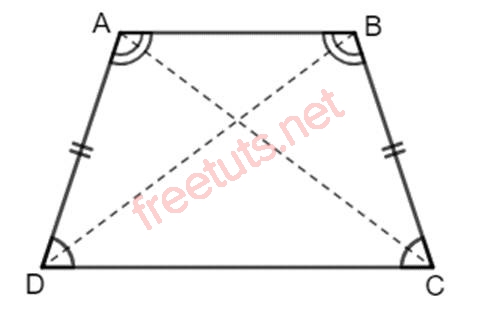
Ví dụ minh họa:
Cho hình thang cân ABCD, ta có:
- Đường chéo AC = đường chéo BD
- Góc A = góc B, góc C = góc D.
- AB song song DC.
- AD = BC.
Dấu hiệu nhận biết hình thang cân
Muốn biết một hình thang có phải là hình thang cân hay không, các em có thể dựa vào các dấu hiệu nhận biết sau:
- Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Hình thang nội tiếp đường tròn cũng là hình thang cân.
Cách chứng minh hình thang cân trong toán học
Dựa vào dấu hiệu nhận biết hình thang cân, các em có 3 phương pháp chứng minh hình thang cân như sau
Cách 1: Chứng minh hình thang có 2 góc kề một đáy bằng nhau là hình thang cân
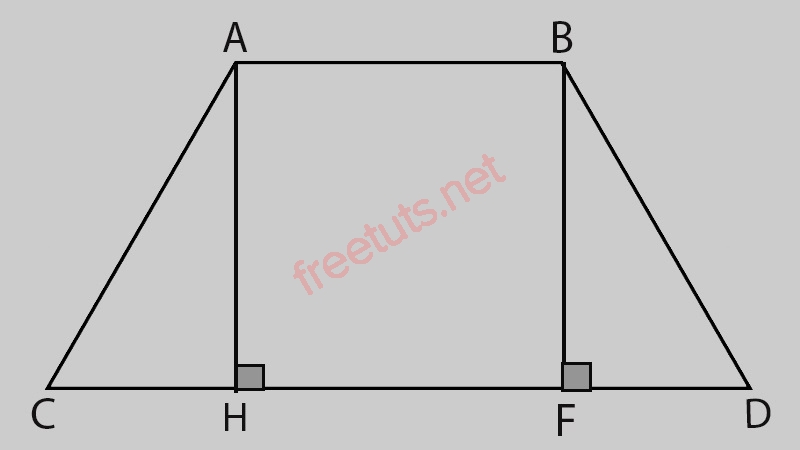
Ví dụ: Cho hình thang ABCD, AB, CD là hai cạnh đáy, biết cạnh bên AD = BC, hãy chứng minh ABCD là hình thang cân.
Lời giải:
Từ điểm A kẻ AH vuông góc với CD, H thuộc CD.
Từ điểm B kẻ BF vuông góc với CD, F thuộc CD.
Lúc này ta có ABFH là hình chữ nhật, cạnh AH = cạnh BF (1)
Xét 2 tam giác AHC và BFD, ta có AC = BD (2)
Từ (1) và (2) ta suy ra tam giác AHC = tam giác BFD, góc ACH = góc BDF,
Suy ra hình thang ABCD có hai góc kề cạnh đáy CD là ACH = BDF, nên ABCD là hình thang cân (điều phải chứng minh)
Cách 2: Chứng minh hình thang có hai đường chéo bằng nhau là hình thang cân
Tiếp theo, freetuts sẽ hướng dẫn chứng minh hình thang cân bằng cách chứng minh hình thang có 2 đường chéo bằng nhau, cụ thể như sau:
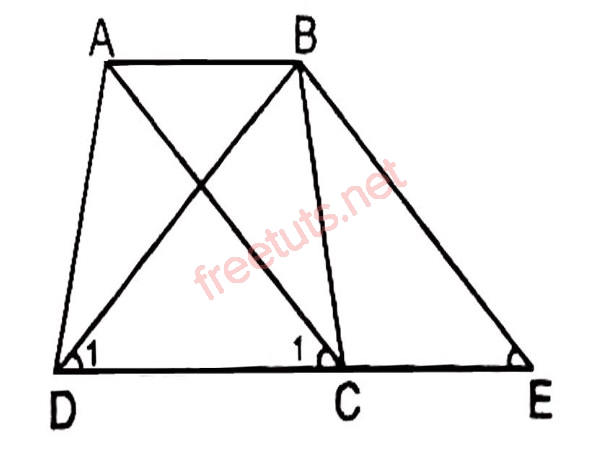
Cho hình thang ABCD, có hai đường chéo AC = BD, hãy chứng minh ABCD là hình thang cân
Lời giải:
Từ đỉnh B, kẻ đường thẳng BE song song với AC và cắt DC tại K.(1)
Có AB // DC, nên suy ra AB // CE (2)
Từ (1) và (2), suy ra ABEC là hình bình hành, nên ta có cạnh CE = AB, AC = BE.
Mà ta có AC = BD, nên suy ra BE = BD.
Xét tam giác BDE có BE = BD nên suy ra tam giác BDE là tam giác cân tại B, nên:
góc E = góc D1. (3)
Xét hình bình hành ABEC, ta có góc E = góc C1 (4)
Từ (3) và (4), suy ra góc D1 = góc C1.
Xét tam giác ACD và tam giác BDC, ta có:
DC là cạnh chung, góc D1 = góc C1, AC = BC
Nên ta có tam giác ACD = tam giác BDC
Vậy góc ADC = góc BCD (2 góc tương ứng)
Xét hình thang ABCD có hai góc kề cạnh đáy DC là góc ADC = góc BCD, nên ABCD là hình thang cân.
Cách 3: Chứng minh hình thang nội tiếp đường tròn là hình thang cân
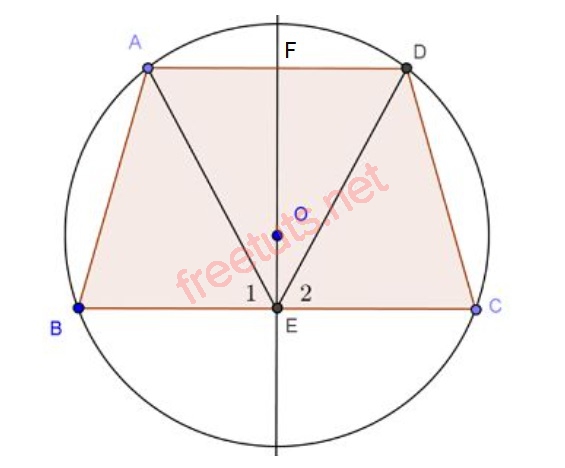
Cho hình thang ABCD nội tiếp đường tròn tâm O. Chứng minh rằng ABCD là hình thang cân.
Gọi E là trung điểm của BC.
Vì O là tâm đường tròn nội tiếp ABCD, nên ta có: OA = OB = OC = OD, nên OE là đường trung trực của BC và AD, OE cắt AD tại F
Xét tam giác vuông AFE, EFD, ta có:
Góc AFE = DFE = 90 độ, cạnh EF chung, cạnh FD = FA
Nên 2 tam giác AFE = tam giác EFD (cạnh góc cạnh)
Suy ra góc AEF = góc DEF (1)
Cạnh AE = DE (2)
Ta có góc E1 + AEF = E2 + góc DEF = 90 độ (3)
Từ (1) và (3), suy ra góc E2 = góc E1.
Xét tam giác ABE và tam giác DCE, ta có:
-
AE = DE (vì tam giác AFE = tam giác EFD)
-
EB = EC (OE là đường trung trực BC)
-
Góc E1 = góc E2
Suy ra tam giác ABE = tam giác DCE
Suy ra góc ABE = góc DCE (4)
Xét hình thang ABCD, có góc ABE = góc DCE nên ABCD là hình thang cân. (điều phải chứng minh)
Lưu ý khi chứng minh hình thang cân
Có một lưu ý quan trọng mà các em cần phải nhớ đó là hình thang cân thì có hai cạnh bên bằng nhau, nhưng một hình thang có hai cạnh bên bằng nhau chưa chắc là hình thang cân vì nó có thể rơi vào 2 trường hợp là hình thoi hoặc hình bình hành như dưới đây:
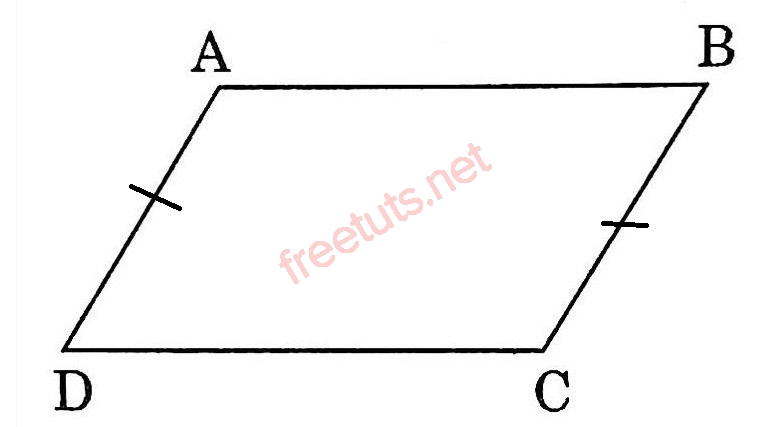
Ví dụ: Hình thang ABCD có cạnh bên AD = DC nhưng ABCD không phải là hình thang cân mà là hình bình hành.
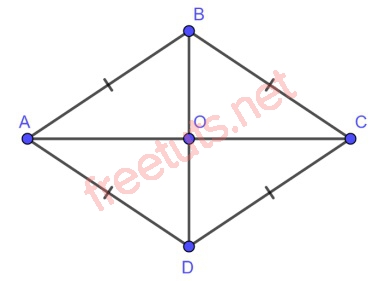
Ví dụ: Hình thang ABCD có cạnh bên AD = DC nhưng ABCD không phải là hình thang cân mà là hình thoi.
Bài tập liên quan đến chứng minh hình thang cân
Như vậy, các em đã nắm được cách chứng minh hình thang cân rồi đúng không nào, bây giờ hãy cùng vận dụng chúng để đi giải một số bài tập sau nha:
- Bài 1: Cho tam giác ABC cân tại A, lấy E thuộc AB, F thuộc AC, AE = AF.
a. Chứng minh BCEF là hình thang cân.
b. Biết A = 70 độ, tính các góc của hình thang cân BCEF
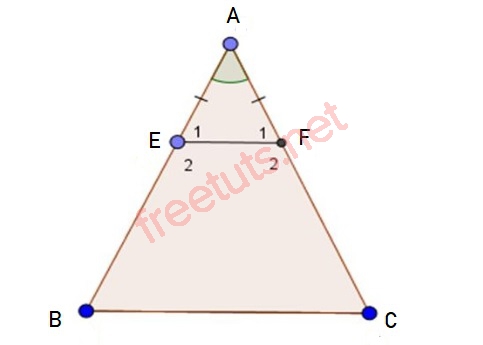
Cách chứng minh hình thang cân trong tam giác cân ABC như sau:
Xét tam giác AEF có AE = AF, suy ra tam giác AEF cân tại A. nên góc E1 = góc F1 (1)
Xét tam giác AEF có:
Góc A + góc E1 + góc F1 = 180 độ (2)
Thế (1) vào (2), ta có:
Góc A + 2 góc E1 = 180 ⟹ Góc E1 = (180 - góc A)/2 (2)
Xét Tam giác ABC có:
Góc A + góc B + góc C = 180 độ, mà góc B = góc C ( vì tam giác ABC cân tại A)
Nên ta có:
Góc A + 2 góc B = 180 ⟹ Góc B = (180 - góc A)/2 (3)
Từ (2) và (3), suy ra: Góc B = góc E1 = (180 - góc A)/2
Mà góc B và góc E1 ở vị trí đồng vị nên ta có EF // BC
⟹ EFBC là hình thang, mà ta có thêm góc B = góc C, nên suy ra:
EFBC là hình thang cân (điều phải chứng minh).
b. Có góc A = 70 độ, thế vào (3), ta có:
Góc B = (180 - 70)/2 = 55 độ.
Góc B = góc C = 55 độ.
Vì FE // BC nên E2 + góc B = 180 độ
⟹ góc F1 = E2 = 180 - góc B = 180 - 55 = 115 độ.
- Bài 2: Cho hình thang cân ABCD, AB // CD, AB < CD, AE và BF là 2 đường cao xuất phát từ đỉnh A và B, E,F thuộc CD. Chứng minh rằng DE = CF.
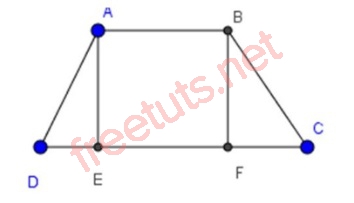
Lời giải:
Xét hình thang cân ABCD, ta có:
AD = BC, góc ADC = góc BCD.
Xét tam giác vuông AED và BFC, ta có:
AD = BC, góc ADC = góc BCD nên suy ra:
Tam giác AED = tam giác BFC, nên ta có DE = CF (điều phải chứng minh)
Như vậy, qua bài viết trên của cuongthinhcorp.com.vn, các em đã nắm được hết cả 3 cách chứng minh hình thang cân rồi đúng không nào. Chúc các em vận dụng những kiến thức này thật tốt để có kết quả học tập cao nha. Chào tạm biệt và hẹn gặp lại các em trong những bài đăng tiếp theo nhé!










