Tính chất tam giác vuông, tam giác cân, tam giác đều, tam giác vuông cân đầy đủ, chi tiết hay nhất | Toán lớp 7

I. Lý thuyết

1. Tam giác vuông

a) Định nghĩa

Tam giác vuông là tam giác có một góc vuông.

b) Tính chất

Trong tam giác vuông hai góc nhọn phụ nhau.

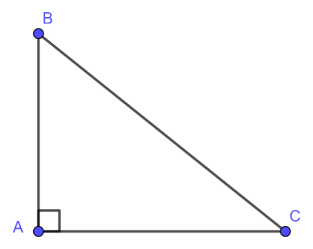
Xét hình vẽ: Tam giác ABC vuông tại A

AB, AC là hai cạnh góc vuông, BC là cạnh huyền.

Ta có: $\widehat{B}+\widehat{C}=90°$

c) Dấu hiệu nhận biết

+ Nếu một tam giác có một góc vuông thì tam giác đó là tam giác vuông.

+ Nếu một tam giác có hai góc phụ nhau thì tam giác đó là tam giác vuông.

2. Tam giác cân

a) Định nghĩa

Tam giác cân là tam giác có hai cạnh bằng nhau.

Hai cạnh bằng nhau gọi là hai cạnh bên, cạnh còn lại là cạnh đáy.

b) Tính chất

+ Tam giác cân có hai cạnh bên bằng nhau.

+ Tam giác cân có hai góc ở đáy bằng nhau.

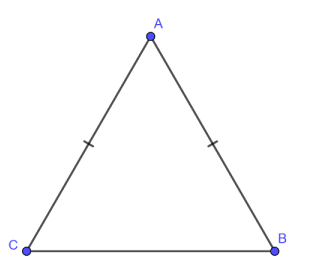
Xét hình vẽ

Tam giác ABC cân tại A ta có:

+ AB, AC là hai cạnh bên.

+ BC là cạnh đáy

Khi đó: $\left\{\begin{array}{l}AB=AC\\ \widehat{B}=\widehat{C}\end{array}\right.$

c) Dấu hiệu nhận biết:

+ Nếu một tam giác có hai góc bằng nhau thì tam gác đó là tam giác cân.

+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

3. Tam giác đều

a) Định nghĩa

Tam giác đều là tam giác có ba cạnh bằng nhau.

b) Tính chất

Nếu một tam giác là tam giác đều thì:

+ Ba góc của tam giác bằng nhau.

+ Ba cạnh của tam giác bằng nhau.

+ Số đo mỗi góc của tam giác là

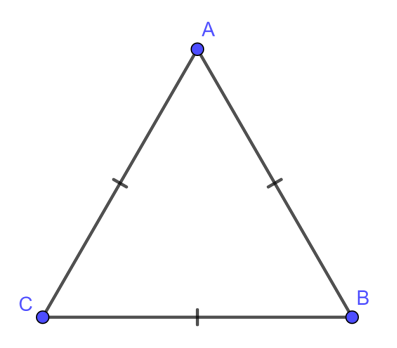
Xét hình vẽ

Tam giác ABC là tam giác đều: $\left\{\begin{array}{l}AB=AC=BC\\ \widehat{A}=\widehat{B}=\widehat{C}=60°\end{array}\right.$

c) Dấu hiệu nhận biết

+ Nếu một tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

+ Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

+ Nếu một tam giác cân có một góc bằng thì tam giác đó là tam giác đều.

4. Tam giác vuông cân

a) Định nghĩa

Tam giác vuông cân là ta giác có một góc vuông và hai cạnh góc vuông bằng nhau.

b) Tính chất

Nếu một tam giác là tam giác vuông cân thì nó có tất cả các tính chất của tam giác vuông và tam giác cân ngoài ra hai góc nhọn trong tam giác vuông cân sẽ bằng nhau và bằng $45°$ .

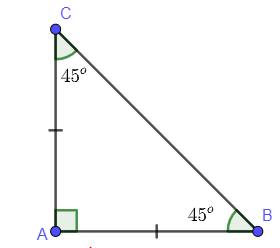
Xét tam giác ABC vuông cân tại A ta có:

+ AB = AC

+ $\widehat{B}=\widehat{C}=45°$

c) Dấu hiệu nhận biết

+ Tam giác vuông có hai cạnh góc vuông bằng nhau là tam giác vuông cân.

+ Tam giác vuông có một góc nhọn bằng  là tam giác vuông cân.

+ Tam giác cân có một góc vuông là tam giác vuông cân.

II. Các ví dụ

Ví dụ 1: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D; trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE cân.

Lời giải:

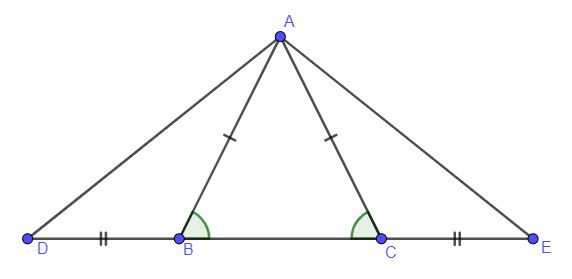
Vì tam giác ABC cân tại A nên $\Rightarrow \left\{\begin{array}{l}AB=AC\\ \widehat{ABC}=\widehat{ACB}\end{array}\right.$    (tính chất)

Vì $\widehat{ABD};\widehat{ABC}$ là hai góc kề bù $\Rightarrow \widehat{ABD}+\widehat{ABC}=180°$

 $\Rightarrow \widehat{ABD}=180°-\widehat{ABC}$ (1)

Vì $\widehat{ACE};\widehat{ACB}$  là hai góc kề bù $\Rightarrow \widehat{ACE}+\widehat{ACB}=180°$

  $\Rightarrow \widehat{ACE}=180°-\widehat{ACB}$ (2)

Mà $\widehat{ABC}=\widehat{ACB}$ (chứng minh trên) (3)

Từ (1); (2); (3) $\Rightarrow \widehat{ABD}=\widehat{ACE}$

Xét tam giác ABD và tam giác ACE có:

$\widehat{ABD}=\widehat{ACE}$ (chứng minh trên)

AB = AC (do tam giác ABC cân tại A)

BD = CE (giả thuyết)

Do đó $\Delta ABD=\Delta ACE$ (c – g – c)

$\Rightarrow AD=AE$ (hai cạnh tương ứng)

Xét tam giác ADE có:

AD = AE (chứng minh trên)

$\Rightarrow$Tam giác ADE cân tại A.

Ví dụ 2: Cho tam giác ABC vuông tại A, $\widehat{B}=30°$. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a) Tam giác BCD là tam giác gì? Vì sao?

b) Chứng minh BC = 2AC.

Lời giải:

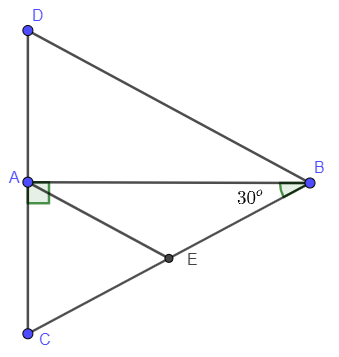
a) Xét tam giác ABC vuông tại A có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lý tổng ba góc trong một tam giác)

$\Rightarrow 90°+30°+\widehat{C}=180°$

$\Rightarrow \widehat{C}=60°$

Xét tam giác ABD và tam giác ABC có:

AB chung

AD = AC (giả thuyết)

$\widehat{DAB}=\widehat{CAB}=90°$

Do đó $\Delta AB\text{D}=\Delta ABC$ (c – g – c)

$\Rightarrow BD=BC$ (hai cạnh tương ứng)

Xét tam giác BDC có:

BD = BC (chứng minh trên)

$\Rightarrow \Delta BDC$cân tại B

Mà $\Delta BDC$ có $\widehat{C}=60°$ $\Rightarrow \Delta BDC$ là tam giác đều.

b) Vì tam giác BDC là tam giác đều nên CD = BC

Xét tam giác BDA và tam giác BA có:

BA chung

BD = BC (do tam giác BDC đều)

$\widehat{BAD}=\widehat{BAC}=90°$

Do đó $\Delta BDA=\Delta BCA$  (cạnh huyền – cạnh góc vuông)

$\Rightarrow DA=AC$

Nên A là trung điểm của CD

$\Rightarrow AC=\frac{1}{2}CD$

Mà CD = BC nên $AC=\frac{1}{2}BC$ (điều phải chứng minh).

Ví dụ 3: Cho tam giác ABC vuông cân tại A. Trên các cạnh góc vuông AB và AC lấy các điểm D và E sao cho AD = AE. Qua D vẽ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh tam giác MDC cân.

Lời giải:

Xét tam giác ADC và tam giác AEB có:

AD = AE (giả thuyết)

$\widehat{DAC}=\widehat{EAB}=90°$

AC = AB (do tam giác ABC vuông cân)

Do đó : $\Delta ADC=\Delta AEB$ (c – g – c)

$\Rightarrow DC=EB$ (hai cạnh tương ứng).         (1)

Gọi G là giao điểm của DK và BE

DG vuông góc với EB tại G.

Xét tam giác DGB vuông tại G có:

$\widehat{GDB}+\widehat{GBD}=90°$ (tính chất)

$\Rightarrow \widehat{GDB}=90-\widehat{GBD}$  (2)

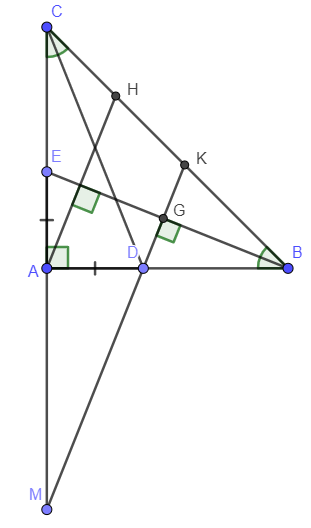
Xét tam giác AEB vuông tại A có:

$\widehat{AEB}+\widehat{ABE}=90°$(tính chất)$\Rightarrow \widehat{AEB}=90°-\widehat{ABE}$   (3)

Từ (2) và (3) $\Rightarrow \widehat{GDB}=\widehat{AEB}$

Lại có $\widehat{GDB}=\widehat{ADM}$ (đối đỉnh)

Nên $\widehat{AEB}=\widehat{ADM}$

Xét hai tam giác AEB và tam giác ADM có:

AE = AD (giả thuyết)

$\widehat{AEB}=\widehat{ADM}$

$\widehat{EAB}=\widehat{DAM}=90°$

Do đó: $\Delta AEB=\Delta ADM$ (góc nhọn – cạnh góc vuông)

$\Rightarrow EB=DM$ (hai cạnh tương ứng)    (4)

Từ (1) và (4) ta có DC = DM

Xét tam giác MDC có:

DM = DC (chứng minh trên)

Do đó tam giác MDC cân tại D.

Xem thêm tổng hợp công thức môn Toán lớp 7 đầy đủ và chi tiết khác:

Công thức Tổng ba góc trong một tam giác chi tiết