Chủ đề chứng minh hai tam giác đồng dạng: Phương pháp chứng minh đồng dạng của hai tam giác là một trong những khái niệm quan trọng trong hình học. Đây là một phương pháp giúp chúng ta làm việc với các tam giác có cấu trúc tương tự nhau và ứng dụng rất linh hoạt trong giải các bài toán hình học. Việc áp dụng phương pháp này giúp chúng ta xác định các hệ số tỉ lệ giữa các cạnh hoặc góc của hai tam giác, từ đó dễ dàng giải quyết các bài toán liên quan đến hình học tam giác một cách nhanh chóng và chính xác.
Làm thế nào để chứng minh hai tam giác đồng dạng?
Để chứng minh hai tam giác đồng dạng, chúng ta có thể sử dụng các phương pháp và định lí sau:
Phương pháp 1: Định lí góc
- Giả sử có hai tam giác ABC và A\'B\'C\' với các đỉnh tương ứng là A, B, C và A\', B\', C\'.
- Để chứng minh hai tam giác đồng dạng, ta cần chứng minh các góc tương ứng của hai tam giác này bằng nhau.
- Vì vậy, ta cần so sánh các góc tương ứng như góc ACB và góc A\'C\'B\' hoặc góc ABC và góc A\'B\'C\'.
- Nếu các góc tương ứng bằng nhau, ta có thể kết luận rằng hai tam giác đồng dạng.
Phương pháp 2: Định lí cạnh
- Giả sử có hai tam giác ABC và A\'B\'C\' với các đỉnh tương ứng là A, B, C và A\', B\', C\'.
- Để chứng minh hai tam giác đồng dạng, ta cần chứng minh tỉ lệ giữa các cạnh tương ứng của hai tam giác này.
- Ví dụ, ta có thể so sánh tỉ lệ giữa cạnh AB và cạnh A\'B\', cạnh BC và cạnh B\'C\', cạnh AC và cạnh A\'C\'.
- Nếu tỉ lệ giữa các cạnh tương ứng bằng nhau, ta có thể kết luận rằng hai tam giác đồng dạng.
Định lí Talet: Nếu hai tam giác có hai cạnh tương ứng tỉ lệ với nhau, và góc tương ứng giữa các cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Định lí Pythagoras: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Đối với từng bài toán cụ thể, chúng ta có thể sử dụng các phương pháp và định lí trên để chứng minh hai tam giác đồng dạng. Quá trình chứng minh có thể đòi hỏi việc sử dụng các bước trung gian và các bằng chứng phụ để hoàn thiện quy trình chứng minh.
Phương pháp nào được sử dụng để chứng minh hai tam giác đồng dạng?
Phương pháp được sử dụng để chứng minh hai tam giác đồng dạng là dựa trên một số quy tắc và định lý. Dưới đây là quy trình cụ thể để chứng minh hai tam giác đồng dạng:
1. Kiểm tra tỉ lệ giữa cạnh và góc vuông của hai tam giác: Để chứng minh hai tam giác đồng dạng, ta cần kiểm tra xem liệu tỉ lệ giữa cạnh và góc vuông của hai tam giác có bằng nhau hay không. Nếu tỉ lệ này được duy trì, ta có thể kết luận rằng hai tam giác đó là đồng dạng. Quy tắc này được gọi là quy tắc tỉ lệ.
2. Sử dụng quy tắc đường thẳng song song: Nếu hai tam giác có các đường thẳng song song, ta có thể sử dụng định lý đường thẳng song song để chứng minh chúng đồng dạng. Định lý này cho biết nếu hai đường thẳng trong một tam giác song song với hai đường thẳng trong tam giác kia, thì tam giác đó là đồng dạng.
3. Sử dụng quy tắc góc: Nếu hai tam giác có các góc tương đương nhau, ta có thể sử dụng quy tắc góc để chứng minh chúng đồng dạng. Quy tắc này cho biết nếu hai góc trong một tam giác bằng với hai góc trong tam giác kia, thì tam giác đó là đồng dạng.
4. Sử dụng quy tắc cạnh: Nếu hai tam giác có các cạnh tương tự nhau hoặc tỉ lệ giữa các cạnh của chúng là như nhau, ta có thể sử dụng quy tắc cạnh để chứng minh chúng đồng dạng. Quy tắc này cho biết nếu tỉ lệ giữa các cạnh của hai tam giác là như nhau, thì tam giác đó là đồng dạng.
5. Sử dụng định lý Talet: Định lý Talet là một công cụ quan trọng để chứng minh hai tam giác đồng dạng. Định lý này chỉ ra rằng nếu ba cạnh của một tam giác chia tỉ lệ tương ứng với ba cạnh của một tam giác khác, thì tam giác đó là đồng dạng.
Qua quá trình kiểm tra và áp dụng các quy tắc và định lý trên, ta có thể chứng minh được hai tam giác có đồng dạng hay không.
Khi nào ta có thể khẳng định rằng hai tam giác là đồng dạng?
Khi xét hai tam giác, chúng ta có thể khẳng định rằng hai tam giác là đồng dạng nếu thỏa mãn một trong những trường hợp sau đây:
1. Quy tắc SS-S: Hai tam giác có cùng hai cạnh xác định và tỉ lệ đúng với nhau sẽ là đồng dạng. Điều này có nghĩa là khi các độ dài của các cạnh tạo thành hai tam giác tỉ lệ với nhau.
2. Quy tắc S-A-S: Hai tam giác có cùng một cạnh xác định, hai góc tạo bởi cạnh đó và hai cạnh khác lần lượt tỉ lệ đúng với nhau, thì hai tam giác là đồng dạng.
3. Quy tắc A-A: Hai tam giác có cùng hai góc định xác định tỉ lệ đúng với nhau, thì hai tam giác là đồng dạng.
4. Định lí Talet: Nếu một tứ giác là một hình thang có hai cạnh tạo thành bởi một góc vuông và một góc nhọn tỉ lệ với các cạnh tạo thành góc nhọn khác trong tam giác, thì hai tam giác là đồng dạng.
Vì vậy, khi chúng ta xác định được rằng các độ dài các cạnh hoặc các góc của hai tam giác có tỉ lệ đúng nhau theo một quy tắc trên, ta có thể kết luận rằng hai tam giác đó là đồng dạng.
Khái niệm hai tam giác đồng dạng - Bài 4 - Toán học 8 - Cô Phạm Thị Huệ Chi
Trên đường tìm hiểu về hai tam giác đồng dạng trong toán học, đừng bỏ lỡ video hấp dẫn này! Bạn sẽ khám phá những công thức và quy tắc đơn giản để xác định các tam giác có đồng dạng hay không. Hãy cùng nhau khám phá và nâng cao kiến thức của bạn!
Làm thế nào để chứng minh hai tam giác đồng dạng dựa trên tỉ lệ cạnh góc vuông?
Để chứng minh hai tam giác đồng dạng dựa trên tỉ lệ cạnh góc vuông, ta có thể làm theo các bước sau đây:
Bước 1: Xác định hai tam giác cần chứng minh đồng dạng. Gọi chúng là tam giác ABC và tam giác DEF.
Bước 2: Kiểm tra xem hai cạnh góc vuông của tam giác ABC có tỉ lệ với hai cạnh góc vuông của tam giác DEF không. Tức là kiểm tra xem các tỉ lệ sau đây có bằng nhau không: \\(\\frac{{AB}}{{DE}} = \\frac{{AC}}{{DF}} = \\frac{{BC}}{{EF}}\\).
Bước 3: Nếu các tỉ lệ trên bằng nhau, tức là \\(\\frac{{AB}}{{DE}} = \\frac{{AC}}{{DF}} = \\frac{{BC}}{{EF}}\\), thì ta có thể kết luận rằng hai tam giác ABC và DEF đồng dạng dựa trên tỉ lệ cạnh góc vuông.
Đây là cách chứng minh hai tam giác đồng dạng dựa trên tỉ lệ cạnh góc vuông. Cần chú ý rằng các cạnh góc vuông của hai tam giác phải tỉ lệ với nhau để có thể kết luận rằng hai tam giác đồng dạng.
Định lí Talet được dùng như thế nào để chứng minh hai tam giác đồng dạng?
Định lí Talet là một trong những phương pháp chứng minh hai tam giác đồng dạng, dựa trên tỉ lệ giữa các cạnh tương ứng của hai tam giác.
Để chứng minh hai tam giác đồng dạng bằng Định lí Talet, ta cần thực hiện các bước sau:
Bước 1: Xác định hai tam giác cần chứng minh đồng dạng. Đặt tên cho các đỉnh của hai tam giác tương ứng (ví dụ: tam giác ABC và tam giác DEF).
Bước 2: Kiểm tra xem tam giác có đúng theo Định lí Talet không. Điều này có nghĩa là hai cạnh tương ứng của hai tam giác cần đồng dạng tỉ lệ với nhau. Đặt các cạnh tương ứng của hai tam giác lại với nhau để xem chúng có tỉ lệ hay không. Ví dụ: (AB/DE) = (AC/DF) = (BC/EF).
Bước 3: Nếu tỉ lệ giữa các cạnh tương ứng của hai tam giác là như nhau, ta kết luận rằng hai tam giác đó đồng dạng.
Bước 4 (Tuỳ chọn): Nếu muốn chứng minh rõ ràng hơn, ta có thể sử dụng các bước chứng minh bổ sung như sử dụng các góc tương ứng, góc sáng tương ứng hay góc giữa hai cạnh để chứng minh hai tam giác đồng dạng.
Lưu ý: Khi chứng minh hai tam giác đồng dạng, cần chú ý đến sự tương ứng giữa các cạnh và các góc tương ứng. Chỉ cần một cặp cạnh và góc tương ứng đồng dạng, ta có thể kết luận rằng hai tam giác đó đồng dạng.

_HOOK_
Cách chứng minh tam giác đồng dạng đơn giản
Bạn cần phần nào đó để chứng minh tam giác đồng dạng một cách dễ dàng? Đừng lo, video này sẽ hướng dẫn bạn cách chứng minh tam giác đồng dạng theo các bước đơn giản và logic. Hãy cùng tham gia để khám phá những bí quyết để làm việc này một cách hiệu quả!
Nếu cạnh huyền và cạnh góc vuông của một tam giác tỉ lệ với cạnh huyền và cạnh góc vuông của một tam giác khác, ta kết luận gì về sự đồng dạng của hai tam giác đó?
Nếu cạnh huyền và cạnh góc vuông của một tam giác tỉ lệ với cạnh huyền và cạnh góc vuông của một tam giác khác, ta có thể kết luận rằng hai tam giác đó là đồng dạng. Điều này được chứng minh bằng Định lí Talet, một trong những phương pháp chứng minh tam giác đồng dạng. Cụ thể, Định lí Talet nói rằng nếu tỉ lệ giữa các cạnh và góc vuông của hai tam giác là như nhau, thì hai tam giác đó đồng dạng với nhau. Điều này có nghĩa là các góc trong hai tam giác sẽ tương ứng và các cạnh sẽ tỉ lệ với nhau theo quy tắc nhất định. Vì vậy, khi cạnh huyền và cạnh góc vuông của hai tam giác tỉ lệ với nhau, ta có thể kết luận rằng hai tam giác đó là đồng dạng.
Khi góc nhọn của một tam giác nhọn được cùng với góc nhọn của một tam giác khác tỉ lệ, hai tam giác đó có phải đồng dạng không?
Để xác định xem hai tam giác có đồng dạng hay không, ta cần kiểm tra xem liệu tỉ lệ giữa góc nhọn của chúng có bằng nhau không.
Để chứng minh điều này, ta có thể thực hiện các bước sau:
Bước 1: Xác định góc nhọn của tam giác đầu tiên (tên là tam giác ABC) và góc nhọn của tam giác thứ hai (tên là tam giác XYZ).
Bước 2: Xác định tỷ số giữa hai góc nhọn bằng cách chia độ lớn của góc nhọn trong tam giác ABC cho độ lớn của góc nhọn trong tam giác XYZ. Nếu tỷ số này là một số hữu tỉ và không phụ thuộc vào kích thước của tam giác, tức là tỷ số không thay đổi khi tam giác này được phóng to hay co lại, thì ta có thể kết luận rằng hai tam giác đồng dạng.
Ví dụ:
Tam giác ABC có góc nhọn ABC và tam giác XYZ có góc nhọn XYZ.
Nếu ta xác định rằng độ lớn của góc ABC là 40 độ và độ lớn của góc XYZ là 20 độ, tức là tỷ số giữa hai góc này là 40/20 = 2.
Nếu ta phóng to hay co lại tam giác ABC và XYZ và xác định lại độ lớn của hai góc nhọn, ta sẽ thấy rằng tỷ số giữa hai góc nhọn vẫn là 2. Điều này cho thấy tỷ số giữa các góc nhọn không thay đổi và không phụ thuộc vào kích thước của tam giác.
Với tỷ số giữa góc nhọn của hai tam giác cố định, ta kết luận rằng hai tam giác này là đồng dạng.
Chú ý rằng phương pháp này chỉ áp dụng cho tam giác nhọn. Trong trường hợp tam giác có góc tù hoặc góc phân giác, cách chứng minh đồng dạng sẽ khác.
Làm thế nào để chứng minh hai tam giác đồng dạng bằng cách sử dụng hai đường thẳng song song?
Để chứng minh hai tam giác đồng dạng bằng cách sử dụng hai đường thẳng song song, ta có thể áp dụng định lí Talet. Định lí Talet nói rằng \"Nếu hai tam giác có cạnh chung và cạnh ngược vuông góc của một tam giác có tỉ lệ tương ứng với cạnh chung và cạnh ngược vuông góc của tam giác kia, thì hai tam giác đó đồng dạng.\"
Dưới đây là các bước để chứng minh hai tam giác đồng dạng bằng cách sử dụng hai đường thẳng song song:
Bước 1: Cho hai tam giác ABC và A\'B\'C\' có hai đường thẳng AB // A\'B\' và BC // B\'C\'.
Bước 2: Chứng minh rằng các góc tương ứng của hai tam giác đó bằng nhau. Ta có:
∠ABC = ∠A\'B\'C\' (Vì AB // A\'B\')
∠BCA = ∠B\'C\'A\' (Vì BC // B\'C\')
Bước 3: Chứng minh rằng tỷ lệ giữa hai cạnh tương ứng của hai tam giác bằng nhau. Ta có:
AB/A\'B\' = BC/B\'C\' (Vì AB // A\'B\' và BC // B\'C\')
Bước 4: Dựa vào định lí Talet đã đề cập ở trên, ta có thể kết luận rằng hai tam giác ABC và A\'B\'C\' đồng dạng.
Tổng kết, để chứng minh hai tam giác đồng dạng bằng cách sử dụng hai đường thẳng song song, ta cần chứng minh rằng các góc tương ứng bằng nhau và tỷ lệ giữa các cạnh tương ứng bằng nhau.
Tại sao chứng minh đồng dạng của hai tam giác là một phương pháp quan trọng trong hình học?
Chứng minh đồng dạng của hai tam giác là một phương pháp quan trọng trong hình học vì nó cho phép chúng ta xác định các đặc tính và quan hệ giữa các tam giác dựa trên các tỉ lệ giữa các cạnh và góc của chúng. Nhờ phương pháp này, chúng ta có thể tìm hiểu và chứng minh các định lý về đồng dạng tam giác, áp dụng chúng vào việc giải quyết các bài toán hình học phức tạp.
Cách chứng minh đồng dạng của hai tam giác thường dựa trên các quy tắc đồng dạng tam giác, bao gồm:
1. Quy tắc cạnh-góc-góc (SAS): Nếu hai cạnh và góc nằm giữa chúng của một tam giác có tỉ lệ tương ứng với hai cạnh và góc nằm giữa chúng của một tam giác khác, thì hai tam giác đó là đồng dạng.
2. Quy tắc cạnh-cạnh-cạnh (SSS): Nếu ba cạnh của một tam giác có tỉ lệ tương ứng với ba cạnh của một tam giác khác, thì hai tam giác đó là đồng dạng.
3. Quy tắc cạnh-góc-cạnh (ASA): Nếu hai cạnh và góc nằm giữa chúng của một tam giác có tỉ lệ tương ứng với hai cạnh và góc nằm giữa chúng của một tam giác khác, thì hai tam giác đó là đồng dạng.
Các phương pháp chứng minh đồng dạng tam giác này cũng có thể được áp dụng để chứng minh đồng dạng của các hình học khác như hình vuông, hình chữ nhật, hình tam giác, và các đa giác. Việc hiểu và áp dụng chúng giúp chúng ta xác định các định lý và quy tắc mới trong hình học, từ đó phát triển các phần tử, hệ thống và lý thuyết mới trong lĩnh vực này.
Tóm lại, chứng minh đồng dạng tam giác là một phương pháp quan trọng trong hình học vì nó giúp chúng ta xác định quan hệ giữa các tam giác dựa trên tỉ lệ giữa cạnh và góc của chúng. Việc áp dụng và chứng minh đồng dạng tam giác cũng góp phần vào việc nghiên cứu và phát triển các định lý và quy tắc mới trong lĩnh vực hình học.
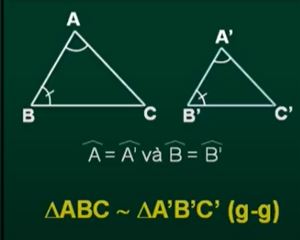
Làm thế nào để áp dụng phương pháp chứng minh đồng dạng tam giác vào việc giải quyết các bài toán thực tế?
Để áp dụng phương pháp chứng minh đồng dạng tam giác vào việc giải quyết các bài toán thực tế, ta cần làm theo các bước sau:
Bước 1: Xác định các yếu tố cần thiết của hai tam giác. Điều này bao gồm đoạn thẳng, cạnh, góc, tỉ lệ cạnh hoặc góc.
Bước 2: Kiểm tra các điều kiện đồng dạng. Các điều kiện này bao gồm:
- Hai cạnh tương tự: Tỷ số cạnh của hai tam giác phải bằng nhau.
- Hai góc tương tự: Góc của hai tam giác phải bằng nhau.
- Hai tỉ số cạnh: Tỷ số cạnh của một tam giác phải bằng tỉ số cạnh của tam giác kia.
Bước 3: Áp dụng các phương pháp chứng minh đồng dạng tam giác để chứng minh sự đồng dạng của hai tam giác. Có một số phương pháp chứng minh đồng dạng tam giác phổ biến:
- Định lý góc: Nếu hai góc tương tự của hai tam giác bằng nhau, ta có thể kết luận hai tam giác đồng dạng.
- Định lý cạnh: Nếu tỷ số cạnh hai tam giác bằng nhau, ta có thể kết luận hai tam giác đồng dạng.
- Định lý tứ giác: Nếu ta có các đường chéo của một tứ giác nào đó chia tứ giác đó thành hai tam giác có tỷ số cạnh tương tự, ta có thể kết luận hai tam giác đồng dạng.
Bước 4: Sau khi chứng minh được sự đồng dạng của hai tam giác, ta có thể áp dụng các thông tin đã biết trong một tam giác để tính toán thông tin về tam giác còn lại.
Tổng hợp lại, để áp dụng phương pháp chứng minh đồng dạng tam giác vào giải quyết các bài toán thực tế, ta cần xác định các yếu tố cần thiết, kiểm tra các điều kiện đồng dạng, áp dụng các phương pháp chứng minh đồng dạng và sau đó sử dụng thông tin đã biết để tính toán các yếu tố còn lại của tam giác.
_HOOK_