Công thức tính độ dài đoạn thẳng trong không gian thường sẽ khác với tính độ dài đoạn thẳng nằm trên một mặt phẳng và phức tạp hơn. Nếu bạn chưa biết cách tính như thế nào, hãy tham khảo bài viết dưới đây của Trung tâm sửa chữa điện lạnh – điện tử Limosa.

1. Định nghĩa về đoạn thẳng trong không gian
- Trong không gian ba chiều, một đoạn thẳng (hoặc còn gọi là đoạn) là một phần của đường thẳng, giới hạn bởi hai điểm đầu cuối. Đoạn thẳng là một đoạn của đường thẳng mà nó bắt đầu từ một điểm và kết thúc tại một điểm khác. Nó được giới hạn bởi hai điểm gọi là điểm đầu và điểm cuối của đoạn thẳng.
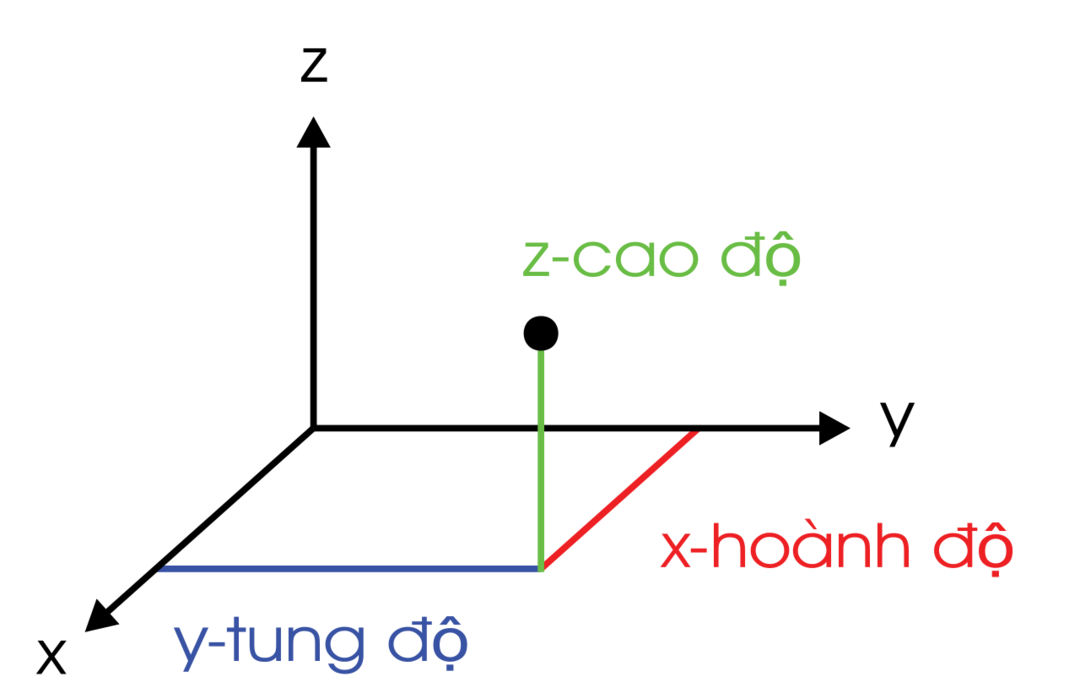
- Để định nghĩa chính xác hơn, một đoạn thẳng trong không gian ba chiều có thể được miêu tả bằng cặp các điểm A(x1, y1,z1) và B(x2,y2,z2) là hai điểm đầu cuối của đoạn thẳng. Độ dài của đoạn thẳng này có thể được tính bằng cách sử dụng công thức khoảng cách giữa hai điểm như đã được mô tả trong câu trước.
- Một ví dụ cụ thể là khi có hai điểm A(1,2,3) và B(4,5,6) trong không gian ba chiều, đoạn thẳng nối hai điểm này là đoạn thẳng AB với điểm đầu A và điểm cuối B, và độ dài của đoạn thẳng AB có thể được tính bằng công thức khoảng cách:
- Tóm lại, đoạn thẳng trong không gian ba chiều là một phần của đường thẳng, giới hạn bởi hai điểm đầu cuối, và độ dài của đoạn thẳng có thể được tính bằng công thức khoảng cách giữa hai điểm.
2. Công thức tính độ dài đoạn thẳng trong không gian chính xác
Trong không gian ba chiều, để tính độ dài của một đoạn thẳng (segment) nối hai điểm A(x1, y1, z1) và B(x2, y2,z2), bạn có thể sử dụng Công thức tính độ dài đoạn thẳng trong không gian như sau:
Công thức khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2,z2) trong không gian ba chiều là: d=((x2−x1)2+(y2−y1)2+(z2−z1)2)
Ở đây, d là khoảng cách giữa hai điểm A và B, và (x1, y1, z1), (x2, y2,z2) là tọa độ của các điểm A và B tương ứng
Lưu ý rằng công thức trên là một trường hợp đặc biệt của công thức khoảng cách Euclid trong không gian nhiều chiều. Đây là một ứng dụng cơ bản của đại số và hình học trong toán học.
Vận dụng của việc áp dụng công thức tính độ dài đoạn thẳng trong không gian
Việc tính độ dài của một đoạn thẳng trong không gian có nhiều ứng dụng trong khoa học, kỹ thuật và cuộc sống hàng ngày. Dưới đây là một số lý do tại sao chúng ta cần tính độ dài đoạn thẳng:
Kỹ thuật và xây dựng: Trong kỹ thuật và xây dựng, việc tính độ dài đoạn thẳng là cần thiết để xác định khoảng cách giữa hai điểm trong không gian. Điều này có thể áp dụng trong thiết kế, xây dựng công trình, lập trình máy CNC, và nhiều ứng dụng khác.
Địa hình và địa lý: Trong địa lý và địa hình, việc tính độ dài đoạn thẳng giữa các điểm trên bề mặt Trái Đất có thể giúp xác định khoảng cách thực tế giữa các vị trí. Điều này quan trọng trong việc định vị và định hướng, đặc biệt trong các ứng dụng GPS và cartography.
Khoa học tự nhiên: Trong nghiên cứu khoa học, tính độ dài đoạn thẳng có thể được sử dụng để xác định khoảng cách giữa các vật thể trong không gian ba chiều, chẳng hạn như quỹ đạo của các thiên thể trong hệ mặt trời.
Tích phân và tính diện tích: Trong tích phân và tính diện tích, việc tính độ dài đoạn thẳng là một phần quan trọng của việc tính diện tích dưới đường cong. Điều này có ứng dụng rộng rãi trong tính toán diện tích bề mặt và thể tích của các hình dạng không gian phức tạp.
Mô hình hóa và mô phỏng: Trong việc mô hình hóa và mô phỏng các hiện tượng thực tế, việc tính độ dài đoạn thẳng giữa các điểm trong không gian có thể giúp tái tạo các tình huống thực tế một cách chính xác hơn.
Tính toán khoảng cách: Trong nhiều tình huống, chẳng hạn như việc tính toán khoảng cách giữa hai vật thể, tính độ dài đoạn thẳng là cần thiết để đưa ra quyết định hoặc tính toán khác.
Tóm lại, công thức tính độ dài đoạn thẳng trong không gian có nhiều ứng dụng thực tế quan trọng trong nhiều lĩnh vực khác nhau, từ kỹ thuật và khoa học tự nhiên đến địa hình và mô hình hóa.

Trên đây là các kiến thức cơ bản về công thức tính độ dài đoạn thẳng trong không gian. Ngoài ra, nếu bạn còn vấn đề gì thắc mắc hay có sản phẩm cần xem xét và sửa chữa, hãy liên hệ cho Trung tâm sửa chữa điện lạnh – điện tử Limosa qua HOTLINE 1900 2276 để được hỗ trợ nhanh chóng tại nhà.
