Công thức tính diện tích hình thang - TRUNG TÂM GIA SƯ TÂM TÀI ĐỨC - HOTLINE: 091 6265 673

Công thức tính chu vi hình thang: thông thường, vuông, cân

Hình thang là 1 trong những tứ giác lồi đem nhị cạnh tuy nhiên song nhưng mà tớ bắt gặp tương đối nhiều vô cuộc sống đời thường hằng ngày. Hai cạnh tuy nhiên song của hình thang được gọi là những cạnh lòng, những cạnh còn sót lại gọi là cạnh mặt mày. Nếu như việc tính chu vi hình thang thì khá dễ dàng ghi nhớ, chỉ đơn giản và giản dị là nằm trong tổng 4 cạnh thì công thức tính diện tích S hình thang lại khó khăn ghi ghi nhớ rộng lớn một chút ít.

Có 3 mô hình thang thông thường bắt gặp là:

Bạn đang xem: Công thức tính diện tích hình thang - TRUNG TÂM GIA SƯ TÂM TÀI ĐỨC - HOTLINE: 091 6265 673

• Hình thang thường
• Hình thang vuông
• Hình thang cân

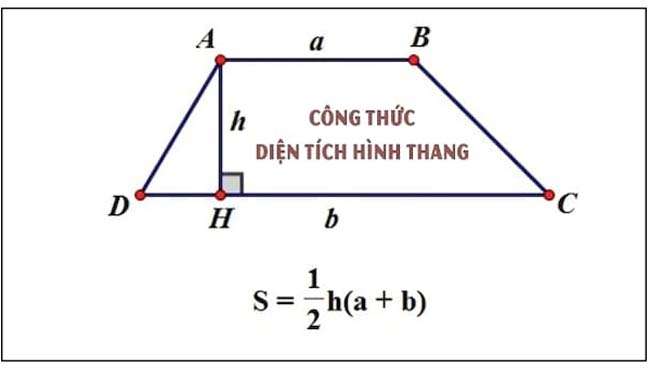
Công thức tính diện tích S hình thang

Khái niệm: Hình thang là 1 trong những tứ giác lồi đem nhị cạnh lòng tuy nhiên tuy nhiên, 2 cạnh còn sót lại được gọi là nhị cạnh mặt mày.

Có hình thang ABCD với phỏng lâu năm lòng AB là a, lòng CD là b và độ cao h.

Công thức tính diện tích S hình thang: trung bình nằm trong 2 cạnh lòng nhân với độ cao đằm thắm 2 lòng.

Trong đó:

• S là diện tích S hình thang.
• a và b là phỏng lâu năm 2 cạnh lòng.
• h là độ cao hạ kể từ cạnh lòng a xuống b hoặc ngược lại (khoảng cơ hội đằm thắm 2 cạnh đáy).

Còn đem bài xích thơ về tính chất diện tích S hình thang khá dễ dàng ghi nhớ như sau:

Muốn tính diện tích S hình thang

Đáy rộng lớn lòng nhỏ tớ đem nằm trong vào

Cộng vô nhân với chiều cao

Chia song lấy nửa thế nào thì cũng ra

Ví dụ:

Một hình thang đem độ cao = 4cm, lòng nhỏ nhắn a = 5cm, lòng rộng lớn b = 12cm. Diện tích hình thang trên?

Áp dụng công thức S = h x ((a +b)/2) = 4 x ((5+12)/2)= 34 (cm).

Còn đem bài xích thơ về tính chất diện tích S hình thang khá dễ dàng ghi nhớ như sau:

Muốn tính diện tích S hình thang

Đáy rộng lớn lòng nhỏ tớ đem nằm trong vào

Cộng vô nhân với chiều cao

Chia song lấy nửa thế nào thì cũng đi ra.

Cách tính diện tích S hình thang vuông

Hình thang vuông là hình thang mang 1 góc vuông. Cạnh mặt mày vuông góc với nhị lòng cũng đó là độ cao h của hình thang.

Công thức công cộng tính diện tích S hình thang vuông tương tự động như hình thang thường: trung bình nằm trong 2 cạnh lòng nhân với độ cao đằm thắm 2 đáy, tuy rằng nhiên chiều cao ở phía trên đó là cạnh mặt mày vuông góc với cả hai lòng.

Trong đó:

• S là diện tích S hình thang.
• a và b là phỏng lâu năm 2 cạnh lòng.
• h là phỏng lâu năm cạnh mặt mày vuông góc với 2 lòng.

Một hình thang vuông ABHD có tính lâu năm lòng nhỏ nhắn lòng rộng lớn theo lần lượt là 8cm, 12cm. Trong số đó đem cạnh AH = 8cm. Hãy tính diện tích S hình thang vuông cơ.

Áp dụng công thức: S = h x ((a + b)/2) = 8 x ((8 + 12)/ 2) = 80cm.

Cách tính diện tích S hình thang cân

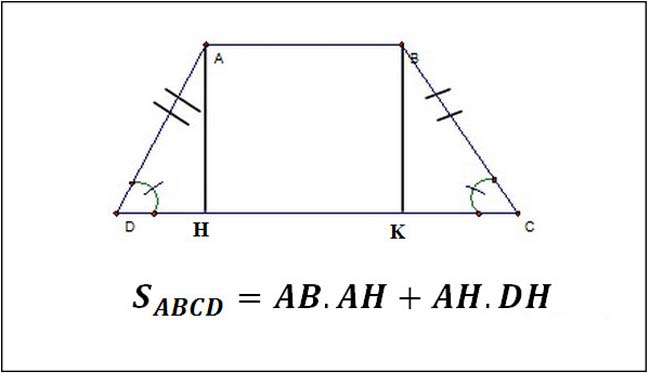
Hình thang cân là hình thang đem nhị góc kề một lòng đều bằng nhau. 2 cạnh mặt mày của hình thang thăng bằng nhau và ko tuy nhiên song cùng nhau.

Ngoài việc vận dụng công thức như tính hình thang thông thường, chúng ta cũng hoàn toàn có thể phân tách nhỏ hình thang cân nặng đi ra nhằm tính diện tích S từng phần rồi nằm trong lại cùng nhau.

Giả dụ, hình thang cân nặng ABCD đem 2 cạnh mặt mày AD và BC đều bằng nhau. Đường cao AH và BK, hình thang sẽ tiến hành chia nhỏ ra trở thành 1 hình chữ nhật ABKH và 2 hình tam giác là ADH và BCK. gí dụng công thức tính diện tích S hình chữ nhật cho tới ABHK và diện tích S tam giác cho tới ADH và BCK tiếp sau đó nằm trong toàn bộ diện tích S nhằm dò xét diện tích S hình thang ABCD.

Cụ thể thế này:

Ví dụ: S = h x ((a + b)/2) = 8 x ((8+16)/2) = 96cm.

S = 2 x S.ACH + S.ABHF = 2 x 50% x 8 x 4 + 8 x 8 = 96cm.

Tính phỏng lâu năm cạnh lòng hình thang

Khi biết diện tích S, độ cao và phỏng lâu năm 1 cạnh lòng, chúng ta cũng có thể tính được phỏng lâu năm cạnh còn sót lại như sau:

AB= 2 x (SABCD/h) - CD

Tính diện tích S hình thang lúc biết 4 cạnh

Ta đem công thức như sau:

Trong đó:

+ a,b: theo lần lượt là phỏng lâu năm 2 cạnh lòng.

+ c,d: theo lần lượt là team lâu năm 2 cạnh mặt mày.

Thực tế nếu như Việc thể hiện thắc mắc phương pháp tính 4 cạnh của hình thang lúc biết 4 cạnh thì tiếp tục không tồn tại đáp án đúng mực vì thế chỉ biết 4 cạnh thì đem thật nhiều tình huống xay đi ra và diện tích S cũng không giống nhau, những chúng ta cũng có thể tưởng tượng ví dụ hình thang tiếp sau đây đem 4 cạnh 4 5 6 9 hoàn toàn có thể vẽ 3 hình dạng không giống nhau với diện tích S không giống nhau.

Tuy nhiên nếu như Việc cho thêm nữa vài ba dữ khiếu nại ví như tính diện tích S hình thang lúc biết phỏng lâu năm 4 cạnh và đem nõi rõ rệt cạnh lòng là cạnh này thì hoàn toàn có thể tính được diện tích S hình thang, ví dụ tất cả chúng ta đem những cạnh đấy Q P.., vô cơ cạnh lòng P.. dài ra hơn nữa và 2 cạnh mặt mày R và S.

Thì hoàn toàn có thể vận dụng công thức tính diện tích S hình thang như sau:

Ngoài đi ra vô tình huống tính diện tích S hình thang lúc biết những cạnh những chúng ta cũng có thể tách đi ra trở thành 2 tam giác và 1 hình chữ nhật hoặc kẻ tăng lối giao phó đằm thắm 2 cạnh mặt mày và vận dụng công thức Heron tính diện tích S tam giác và suy đi ra được diện tích S hình thang. Công thức bên trên cũng rất được tạo hình kể từ phương pháp này.

Công thức heron tính diện tích S tam giác

Gọi S là diện tích S và phỏng lâu năm 3 cạnh tam giác theo lần lượt là a, b và c

Công thức Heron còn hoàn toàn có thể được viết lách lại bằng

Lưu Ý Khi Giải Các Bài Tập Về Tính Diện Tích Hình Thang

– Trong quy trình giải toán, nhiều bậc cha mẹ, nhiều chúng ta học viên do dự ko biết “hình thang hoàn toàn có thể tích hoặc không? Công thức tính thể tích hình thang cân nặng thế nào?“. Với thắc mắc này, những các bạn sẽ ko thể tìm kiếm được đáp án vấn đáp vì thế hình thang là nhiều giác vô hình học tập bằng phẳng, ko hoàn toàn có thể tích như hình không khí.

– Tại hình học tập cung cấp 2, chúng ta học viên tiếp tục kế tiếp được tiếp cận với những dạng toán về hình thang. Tuy nhiên, những bài xích tập dượt thời điểm hiện nay không chỉ là đơn giản và giản dị là tính chu vi, diện tích S nhưng mà yên cầu sự trí tuệ thâm thúy, phối hợp những đặc điểm về góc (tổng 2 góc kề 1 lòng vô hình thang bằng 180°), tính hóa học những cạnh mặt mày, đặc điểm về lối khoảng của hình thang,… Tuy nhiên, ở cung cấp tè học tập, chúng ta chỉ việc bắt được những công thức tính diện tích S hình thang kể bên trên là tiếp tục hoàn toàn có thể giải được đa số những Việc vô công tác học tập của tớ rồi.

Bài tập dượt hình thang, diện tích S hình thang

Cho hình chữ nhật ABCD đem diện tích S là 15cm2, AB = 5cm. Cho E phía trên đường thẳng liền mạch DC với C nằm trong lòng D và E và phỏng lâu năm DE = 7cm. Tính diện tích S hình ABED.

Giải:

Theo đề bài xích thể hiện, tớ đem chừng như sau:

ABCD là hình chữ nhật, E phía trên DC nên AB // DE, góc ADC = 90 độ

=> ABED là hình thang vuông

Tính cạnh AD = SABCD : AB = 15 : 5 = 3cm

Do cơ, Diện tích hình thang vuông ABED = AD . (AB + DE) : 2 = 3 . ( 5 + 7) : 2 = 18cm2

Ví dụ cho 1 hình thang đem chiều lâu năm cạnh a= 20cm, cạnh b= 14cm và độ cao nối kể từ đỉnh hình mon xuống lòng là 12cm. Hỏi diện tích S hình thang là bao nhiêu?

Cách giải: Có a= trăng tròn centimet, b = 14cm, h=25cm. Hỏi S=?

Dựa theo dõi công thức tính diện tích S hình thang, tớ có:

S = h x (a +b/2) hoặc 50% (a+b) x h

S = 12 x ((20 + 14)/2) hoặc 50% x (20+14) x 25

S = 50% x 34 x 25 = 425 centimet.

Như vậy phụ thuộc công thức tính diện tích S hình thang, tất cả chúng ta hoàn toàn có thể dò xét đi ra diện tích S hình thang bởi vì 425 centimet.

Cho hình chữ nhật ABCD đem diện tích S là 15cm2, AB = 5cm. Cho E phía trên đường thẳng liền mạch DC với C nằm trong lòng D và E và phỏng lâu năm DE = 7. Tính diện tích S hình ABED.

Giải:

Xem thêm: Nui tiếng Anh là gì? - tieng-nhat.com

Theo đề bài xích thể hiện, tớ đem chừng như sau:
ABCD là hình chữ nhật, E phía trên DC nên AB // DE, góc ADC = 90 độ

=> ABED là hình thang vuông
Tính cạnh AD = SABCD : AB = 15 : 5 = 3cm
Do cơ, Diện tích hình thang vuông ABED = AD . (AB + DE) : 2 = 3 . ( 5 + 7) : 2 = 18cm2

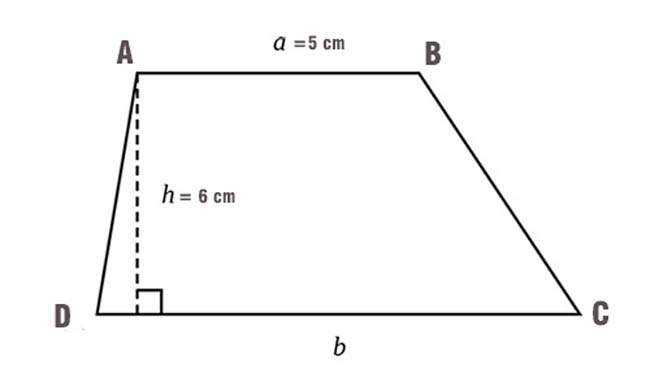
Bài toán: Có hình thang ABCD đem lòng nhỏ AB = 5 centimet, lòng rộng lớn DC lâu năm gấp hai lòng nhỏ. Chiều cao của hình thang AH = 6 centimet. Tính diện tích S hình thang.

Cách tính diện tích S hình thang

Kiến thức về hình thang khá thịnh hành với chúng ta học viên cung cấp 1. Để ôn lại những Việc tương quan cho tới tính diện tích S hình thang, mời mọc chúng ta theo dõi dõi những vấn đề và ví dụ minh họa tức thì tiếp sau đây.

Trước không còn tớ cần thiết khái niệm hình thang là gì? Hình thang là tứ giác lồi đem 2 cặp cạnh đối lập tuy nhiên song cùng nhau và đấy là 2 cạnh lòng, 2 cạnh đối lập còn sót lại là 2 cạnh mặt mày. Các đặc điểm không giống của hình thang gồm những: 2 góc kề đem tổng bởi vì 360 phỏng, đường thẳng liền mạch nối trung điểm của 2 cạnh mặt mày được gọi là lối khoảng của hình thang.

Các mô hình thang gồm: Hình thang vuông (hình thang có một góc vuông), hình thang cân nặng (hình thang đem 2 cạnh kề bởi vì nhau), hình thang vuông cân nặng (chính là hình chữ nhật).

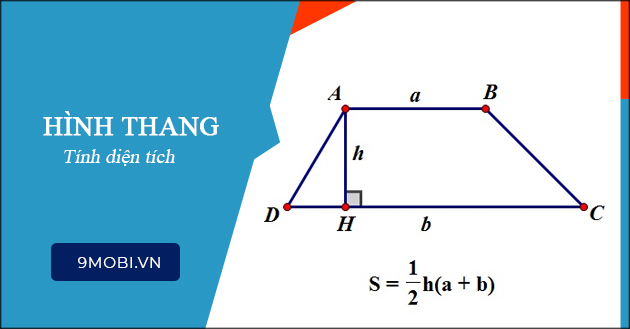
CÁCH TÍNH DIỆN TÍCH HÌNH THANG

Công thức tính diện tích S hình thang: S = 1⁄2 h (a + b) (Diện tích hình thang bởi vì 1/2 tích của tổng 2 lòng và độ cao ứng với 2 cạnh lòng, đơn vị chức năng diện tích S là mét vuông).

Giải mến công thức:

S: Diện tích hình thang

a, b: Độ lâu năm 2 lòng của hình thang

h: Độ lâu năm lối cao

Để dễ dàng ghi nhớ phương pháp tính diện tích S hình thang, chúng ta cũng có thể học tập nằm trong lòng cay đắng thơ sau:

Muốn tính diện tích S hình thang

Đáy rộng lớn, lòng nhỏ tớ đem nằm trong vào

Rồi đem nhân với lối cao

Chia song sản phẩm thế nào thì cũng đi ra.

Dưới đấy là ví dụ minh họa khiến cho bạn vận dụng công thức tính diện tích S hình thang.

Bài toán: Có hình thang ABCD đem lòng nhỏ AB = 5 centimet, lòng rộng lớn DC lâu năm gấp hai lòng nhỏ. Chiều cao của hình thang AH = 6 centimet. Tính diện tích S hình thang.

Giải:

Bài toán cho tới biết:

AB = 5 cm

DC lâu năm gấp hai AB, suy đi ra DC = 10 cm

AH = 6 cm

Áp dụng tức thì công thức tính diện tích S hình thang tớ được luật lệ tính:

S = 1⁄2 h (a + b) = 1⁄2 x 6 x (5 + 10) = 40 cm2

Đáp số: 40 cm2

Câu 1. Cho hình thang ABCD có tính lâu năm lối cao là 4,2 dm, diện tích S = 36,12 dm² và lòng rộng lớn CD dài ra hơn nữa lòng nhỏ nhắn AB là 7,8 dm. Kéo lâu năm AD và BC tách nhau bên trên E. hiểu AD = 3/5 DE. Hỏi diện tích S hình tam giác ABE là bao nhiêu?

Câu 2. Cho hình thang ABCD. Bốn điểm M, N, P.., Q theo lần lượt là trung điểm của những cạnh AB, BC, CD, DA. hiểu diện tích S tứ giác MNPQ là 115 cm². Tính diện tích S hình thang ABCD.

Câu 3. Cho hình thang vuông ABCD (góc A, D là góc vuông) đem AB=4cm, DC=5cm, AD=3cm. Nối D với B được nhị hình tam giác ABD và BDC.

a) Tính diện tích S hình tam giác cơ.

b) Tính tỉ số xác suất của diện tích S hình tam giác ABD và diện tích S hình tam giác BDC.

Câu 4. Tính diện tích S hình thang đem :

a). Đáy rộng lớn 8m; lòng nhỏ nhắn 75dm; độ cao 32dm.

b). Đáy rộng lớn 1,9m; lòng nhỏ nhắn 1,3m; độ cao 0,9m.

c). Đáy rộng lớn 2/3m; lòng nhỏ nhắn 1/2m; độ cao 3/5m.

Câu 5. Tính độ cao hình thang có:

a). Diện tích 30cm²; lòng rộng lớn 8cm và lòng nhỏ nhắn 0,4dm.

b). Diện tích 6,4 dm²; lòng rộng lớn 1,8dm; lòng nhỏ nhắn 1,4dm.

c). Diện tích 3/4m²; lòng rộng lớn 1/4m và lòng nhỏ nhắn 1/8m.

Câu 6. Tính tổng nhị lòng hình thang có:

a). Diện tích 3,6 dam²; độ cao 1,2dam.

b). Diện tích 3/4m²; độ cao 2/3m.

c). Diện tích 2400cm²; độ cao 3,8dm.

Câu 7. Một miếng khu đất hình thang đem lòng nhỏ nhắn 18m và bởi vì ¾ lòng rộng lớn. Tính diện tích S miếng khu đất hình thang?

Câu 8. Một thửa ruộng hình thang vuông đem cạnh mặt mày vuông góc với 2 lòng lâu năm 30,5m; lòng rộng lớn 120,4m; lòng nhỏ nhắn 79,6m.

a. Tính diện tích S thửa ruộng bởi vì dam²

b. Trung bình 100dam² thu được 65,2kg thóc. Hỏi bên trên cả thửa ruộng nhận được từng nào kilogam thóc?

Câu 9. Một hình thang đem tổng nhị lòng 110cm. Tổng của lòng rộng lớn và độ cao 114cm. Tổng của lòng nhỏ nhắn và độ cao là 68cm. Tính diện tích S hình thang?

Câu 10. Một hình thang đem lòng nhỏ nhắn 2,8dm.Đáy rộng lớn bởi vì 7/3 lòng nhỏ nhắn và bởi vì 5/3 độ cao. Tính diện tích S hình thang.

Câu 11. Một thửa ruộng hình thang đem lòng rộng lớn 140m và bởi vì 4/3 lòng nhỏ nhắn, độ cao 56,4m. Tính đi ra cứ 5dam² thì thu hoạch được 320kg thóc. Hỏi cả thửa ruộng nhận được từng nào tấn thóc?

Câu 12. Một miếng khu đất hình thang đem tổng lòng rộng lớn, lòng nhỏ nhắn và độ cao là 90m. Đáy nhỏ nhắn bởi vì 3/4 lòng bé; độ cao bởi vì ½ lòng rộng lớn. hiểu rằng cứ 2 dam² thì rất cần phải bón 50kg phân. Hỏi bón cả thửa ruộng thì rất cần phải đem từng nào tạ phân?

Câu 13. Một thửa ruộng hình thang đem lòng rộng lớn 75,6m; lòng nhỏ nhắn 62,4m và độ cao 40m. hiểu rằng 2/5 diện tích S thửa ruộng trồng ngô, 1/3 diện tích S trồng khoai, còn sót lại trồng lạc. Tính diện tích S trồng từng loại cây trên?

Công Thức Tính Chiều Cao Hình Thang, Đáy Lớn, Đáy Nhỏ Hình Thang

Với công thức tính diện tích S hình thang phía trên, tớ cũng hoàn toàn có thể đơn giản dễ dàng giải những bài xích tập dượt nâng lên về hình thang: tính độ cao hình thang lúc biết diện tích; tính lòng rộng lớn, lòng nhỏ hình thang lúc biết diện tích S như sau:  

Công thức tính độ cao hình thang lúc biết diện tích S, chiều lâu năm 2 cạnh

Công thức tính tổng nhị lòng của hình thang lúc biết diện tích S, chiều cao

Công thức toán

Gia sư môn toán

Xem thêm: 100+ Từ vựng các loại trái cây bằng tiếng Anh cho bé

Công thức tính diện tích S hình bình hành

Công thức tính diện tích S hình thang

Công thức tính diện tích S hình thoi