TÂM ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC - NHỮNG ĐIỀU CẦN NẮM RÕ
Bộ môn Toán 9 học sinh cần nắm được đường tròn, đặc biệt tâm đường tròn ngoại tiếp tam giác. Cunghocvui.com hiểu được điều đó nên đã đưa ra tổng hợp những kiến thức bổ ích cho các em. Đường tròn ngoại tiếp tam giác là gì? Công thức tính bán kính, xác định tâm đường tròn ngoại tiếp...sẽ có trong bài viết.
1. Khái niệm đường tròn ngoại tiếp tam giác
- Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Có thể nói theo cách khác là tam giác nội tiếp đường tròn.
- Ví dụ về đường tròn ngoại tiếp tam giác:
.png)
Ví dụ về đường tròn ngoại tiếp tam giác
Đường trung trực của đoạn thẳng AB là đường thẳng đi qua trung điểm M của AB, vuông góc với AB. Mọi điểm I thuộc trung trực AB đều có IA = IB.
Ba đường trung trực tam giác đồng quy tại một điểm. Gọi I là giao điểm của ba đường trung trực giam giác ABC thì ta có IA = IB = IC, I là tâm đường tròn ngoại tiếp tam giác ABC. Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
- Cách vẽ đường tròn ngoại tiếp tam giác:
Cách vẽ đường tròn ngoại tiếp tam giác nhọn
2. Khái niệm và tính chất tâm đường tròn ngoại tiếp tam giác
Tâm đường tròn ngoại tiếp tam giác là giao điểm của 3 đường gì?
- Tâm của đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của ba cạnh tam giác (có thể là giao điểm hai đường trung trực).
- Cách xác định tâm đường tròn ngoại tiếp tam giác:
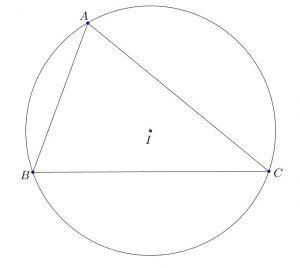
Xác định tâm đường tròn ngoại tiếp tam giác
+ Cách 1:
Bước 1: Viết phương trình đường trung trực hai cạnh bất kỳ tam giác.
Bước 2: Tìm giao điểm hai đường trung trực, chính là tâm đường tròn ngoại tiếp tam giác.
+ Cách 2:
Bước 1: Gọi I (x, y) là tâm đường tròn ngoại tiếp tam giác ABC. Ta có IA = IB = IC = R.
Bước 2: Tìm tọa độ tâm đường tròn ngoại tiếp tam giác:
Tọa độ tâm I là nghiệm của phương trình: \(\left\{\begin{matrix}IA^2 = IB^2 & \\ IA^2 = IC^2& \end{matrix}\right.\)
Tâm đường tròn ngoại tiếp tam giác cân ABC tại A nằm trên đường cao AH.
Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.
Tâm đường tròn ngoại tiếp tam giác đều là trọng tâm của tam giác.
3. Bán kính đường tròn ngoại tiếp tam giác
Ngoài các công thức liên quan tới đường tròn, các em cần nắm được công thức tính bán kính đường tròn ngoại tiếp tam giác.
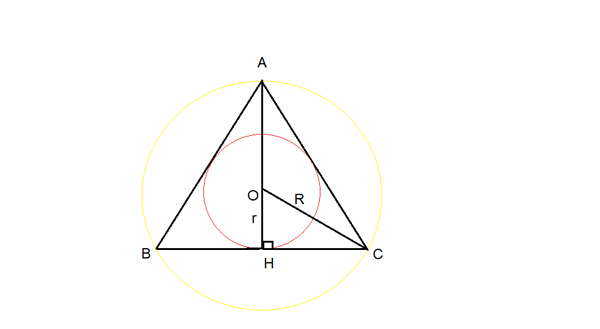
Bán kính đường tròn ngoại tiếp tam giác
Cho tam giác ABC. Độ dài các cạnh BC, AC, AB lần lượt là a, b, c.
- Công thức cách tính bán kính đường tròn ngoại tiếp tam giác:
\(R = \frac{a.b.c}{4S}\)
+ Công thức tính diện tích tam giác (áp dụng công thức herong):
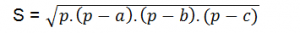
+ Nửa chu vi tam giác:
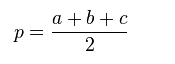
+ Công thức tính bán kính đường tròn nội tiếp tam giác:
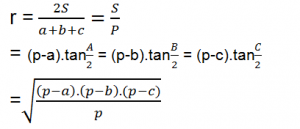
- Công thức tính bán kính đường tròn ngoại tiếp góc A:
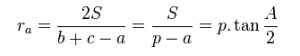
- Công thức tính bán kính đường tròn ngoại tiếp góc B:
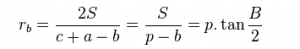
- Công thức tính bán kính đường tròn ngoại tiếp góc C:
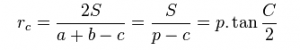
- Công thức tính bán kính đường tròn ngoại tiếp tam giác đều:
R = \(\frac{a}{2sin60^{0}}\), trong đó a là độ dài mỗi cạnh.
Sau khi học xong lý thuyết, các em học sinh có thể tham khảo các bài tập liên quan tới đường tròn.
Trên đây là toàn bộ nội dung về tâm đường tròn ngoại tiếp tam giác, rất mong đem lại quý độc giả những thông tin bổ ích!










