Dạng 1: Áp dụng công thức tính công suất

Sau khi tham gia học xong xuôi bài xích này, những em rất cần được tóm được một số kỹ năng và kiến thức sau:

• Viết được công thức tính hiệu suất và thông số hiệu suất mang đến đoạn mạch năng lượng điện xoay chiều .

  Bạn đang xem: Dạng 1: Áp dụng công thức tính công suất

• Nêu được khái niệm và vai trò của thông số hiệu suất .

Hôm ni tất cả chúng ta qua quýt dạng thứ nhất của bài xích Công suất, dạng 1 sát dụng công thức tính hiệu suất.

* Các công thức tính công suất
+ Công thức lăm le nghĩa: \(P = \frac{U_0I_0}{2}\cos \varphi = UI\cos \varphi\)
+ Công thức thông thường sử dụng:
\(P = UI\cos \varphi = I.Z.I.\frac{R}{Z} = RI^2\)
\(\Rightarrow Phường = RI^2 = R.\frac{U^2}{R^2 + (Z_L-Z_C)^2}\)
+ Công thức quánh biệt:
\(P = UI\cos \varphi = U.\frac{U}{Z}.\frac{R}{R}.\cos \varphi = \frac{U^2}{R}\cos ^2 \varphi\)
\(\Rightarrow Phường = \frac{U^2}{R}\cos ^2 \varphi\)
* Hệ số công suất: \(\cos \varphi = \frac{R}{Z} = \frac{R}{\sqrt{R^2 + (Z_L - Z_C)^2}}\)
NHỚ: \(-\frac{\pi }{2} \leq \varphi = \varphi _u - \varphi _i \leq \frac{\pi }{2} \Rightarrow 0 \leq \cos \varphi \leq 1\)

VD1: Đặt năng lượng điện áp \(u = 200\sqrt{2}\cos (100\pi t - \frac{\pi}{3})\) (V) vô 2 đầu đoạn mạch thì độ mạnh loại năng lượng điện qua quýt mạch là \(i = 2\sqrt{2}\sin (100\pi t + \frac{\pi}{2})\) (A). Tìm cos \(\varphi\), P?
Giải:
Ta có: \(\left\{\begin{matrix} u = 200\sqrt{2}\cos (100\pi t - \frac{\pi}{3}) \hspace{2,8cm}\\ i = 2\sqrt{2}\sin (100\pi t + \frac{\pi}{2}) = 2\sqrt{2}\cos (100\pi t) \end{matrix}\right.\)
\(\cdot \ \varphi = \varphi _u + \varphi _i = - \frac{\pi }{3} - 0 = - \frac{\pi }{3} \Rightarrow \cos = \frac{1}{2}\)
\(\cdot \ Phường = \frac{U_0I_0}{2} \cos \varphi = \frac{200\sqrt{2}.2\sqrt{2}}{2}.\frac{1}{2} = 200\ (W)\)

VD2: Đặt năng lượng điện áp \(u = 120\sqrt{2}\cos(100 \pi t)\) (V) vô 2 đầu đoạn mạch RLC ghép tiếp nối đuôi nhau có \(R = 30\ (\Omega );\ L = \frac{3}{5 \pi }\ (H);\ C = \frac{10^{-3}}{9\pi }\ (F)\). Tìm Phường, cos \(\varphi\)?
Giải:
\(Z_L = L\omega = \frac{3}{5\pi }.100 \pi = 60\ \Omega\)
\(Z_C = \frac{1}{C\omega } = \frac{1}{\frac{10^{-3}}{9\pi }}.100 \pi = 90\ \Omega\)
\(\cdot \ Phường = R.\frac{U^2}{R^2 + (Z_L-Z_C)^2} = 30.\frac{120^2}{30^2 + (60-90)^2} = 240\ (W)\)
\(\cdot \ \cos \varphi = \frac{R}{\sqrt{R^2 + (Z_L - Z_C)^2}} = \frac{30}{\sqrt{30^2 + (60-90)^2}} = \frac{1}{\sqrt{2}}\)

VD3: Đặt 1 năng lượng điện áp xoay chiều có mức giá trị hiệu dụng 100 V vô 2 đầu mạch RLC ghép tiếp nối đuôi nhau có \(R = 50\ \Omega\) thì năng lượng điện áp nhì đầu mạch chếch pha \(\frac{\pi}{3}\) so với năng lượng điện áp 2 đầu tụ C. Tìm Phường, cos \(\varphi\)?
Giải:

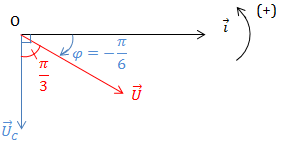
\(\cdot \ Phường = \frac{U^2}{R}.\cos ^2 \varphi\)
\(\rightarrow Phường = \frac{100^2}{50}.\cos^2\left ( -\frac{\pi}{6} \right ) = 150 \ (W)\)
\(\cdot \ \cos \varphi = \cos \left ( -\frac{\pi}{6} \right ) = \frac{\sqrt{3}}{2}\)

Xem thêm: "Phơi Quần Áo" trong Tiếng Anh là gì: Định Nghĩa, Ví Dụ Anh Việt