PHẦN II. MẶT NÓN - MẶT TRỤ - MẶT CẦU
1. MẶT NÓN TRÒN XOAY VÀ KHỐI NÓN
1.1. Mặt nón tròn xoay
|
Nội dung |
Hình vẽ |
|
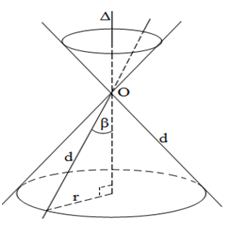
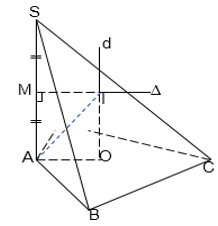
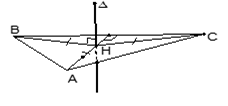
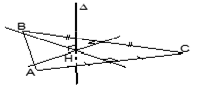
Đường thẳng $d,\ \Delta $ cắt nhau tại $O$ và tạo thành góc $\beta $ với ${{0}^{o}}<\beta <{{90}^{o}},\ mp\left( P \right)$ chứa $d,\ \Delta .\ \left( P \right)$ quay quanh trục $\Delta $với góc $\beta $ không đổi $\Rightarrow $ mặt nón tròn xoay đỉnh $O$
|
|
1.2. Khối nón
|
Nội dung |
Hình vẽ |
|
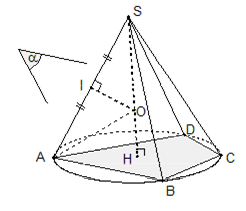
Là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó. Những điểm không thuộc khối nón gọi là những điểm ngoài của khối nón. Những điểm thuộc khối nón nhưng không thuộc hình nón tương ứng gọi là những điểm trong của khối nón. Đỉnh, mặt đáy, đường sinh của một hình nón cũng là đỉnh, mặt đáy, đường sinh của khối nón tương ứng. |
|
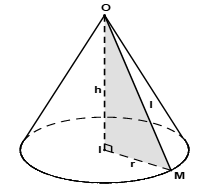
Cho hình nón có chiều cao $h,$ đường sinh $l$ và bán kính đáy$r$.
- Diện tích xung quanh: của hình nón:
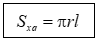
- Diện tích đáy (hình tròn): $S$đáy$=\pi {{r}^{2}}$
- Diện tích toàn phần: của hình nón: ${{S}_{tp}}=\pi rl+\pi {{r}^{2}}$
- Thể tích khối nón: $V=\frac{1}{3}\pi {{r}^{2}}h$
1.3. Thiết diện khi cắt bởi mặt phẳng
|
Điều kiện |
Kết quả |
|
Cắt mặt nón tròn xoay bởi mp $\left( Q \right)$ đi qua đỉnh của mặt nón. |
|
|
|
|
Cắt mặt nón tròn xoay bởi mp ( Q ) không đi qua đỉnh của mặt nón. |
|
|
|
2. MẶT TRỤ TRÒN XOAY
2.1. Mặt trụ
|
Nội dung |
Hình vẽ |
|
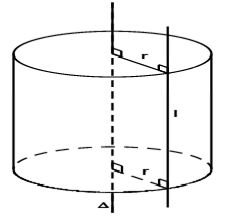
Trong mặt phẳng $\left( P \right)$ cho hai đường thẳng $\Delta $ và $l$ song song với nhau, cách nhau một khoảng bằng $r$. Khi quay mặt phẳng $\left( P \right)$ xung quanh $\Delta $ thì đường thẳng $l$ sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay, gọi tắt là mặt trụ.
|
|
2.2. Hình trụ tròn xoay và khối trụ tròn xoay
|
Nội dung |
Hình vẽ |
|
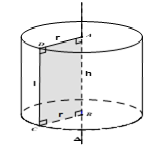
Ta xét hình chữ nhật $ABCD$. Khi quay hình chữ nhật $ABCD$ xung quanh đường thẳng chứa một cạnh nào đó, chẳng hạn cạnh AB thì đường gấp khúc $ABCD$ sẽ tạo thành một hình gọi là hình trụ tròn xoay, hay gọi tắt là hình trụ. |
|
- Khi quay quanh $AB,$ hai cạnh $AD$ và $BC$ sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ, bán kính của chúng gọi là bán kính của hình trụ.
- Độ dài đoạn $CD$ gọi là độ dài đường sinh của hình trụ.
- Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh $CD$ khi quay xung quanh $AB$ gọi là mặt xung quanh của hình trụ.
- Khoảng cách $AB$ giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.
Khối trụ tròn xoay hay khối trụ là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ tròn xoay đó. Những điểm không thuộc khối trụ gọi là những điểm ngoài của khối trụ. Những điểm thuộc khối trụ nhưng không thuộc hình trụ tương ứng gọi là những điểm trong của khối trụ. Mặt đáy, chiều cao, đường sinh, bán kính của một hình trụ cũng là mặt đáy, chiều cao, đường sinh, bán kính của khối trụ tương ứng.Hình trụ có chiều cao $h,$ đường sinh $l$ và bán kính đáy $r.$
- Diện tích xung quanh: ${{S}_{xq}}=2\pi rl$
- Diện tích toàn phần: ${{S}_{tp}}=2\pi rl+2\pi {{r}^{2}}$
- Thể tích: $V=\pi {{r}^{2}}h$
3. MẶT CẦU – KHỐI CẦU
3.1. Mặt cầu
|
Nội dung |
Hình vẽ |
|
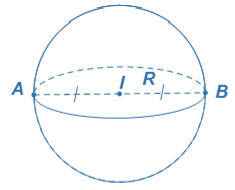
Cho điểm $I$ cố định và một số thực dương $R$. Tập hợp tất cả những điểm $M$ trong không gian cách $I$ một khoảng $R$ được gọi là mặt cầu tâm $I,$ bán kính $R.$ Kí hiệu: $S\left( I;R \right)$ Khi đó: $S\left( I;R \right)=\left\{ M|IM=R \right\}$ |
|
3.2. Vị trí tương đối giữa mặt cầu và mặt phẳng
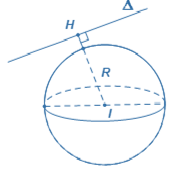
Cho mặt cầu $S\left( I;R \right)$ và mặt phẳng $\left( P \right)$. Gọi $H$ là hình chiếu vuông góc của $I$ lên $\left( P \right)\Rightarrow d=IH$ là khoảng cách từ $I$ đến mặt phẳng $\left( P \right)$. Khi đó:
|
$d>R$ |
$d=R$ |
$d<R$ |
|
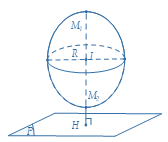
Mặt cầu và mặt phẳng không có điểm chung. |
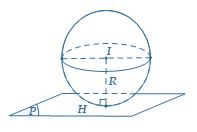
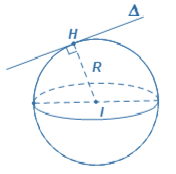
Mặt phẳng tiếp xúc mặt cầu: $\left( P \right)$ là mặt phẳng tiếp diện của mặt cầu và $H:$ tiếp điểm. |
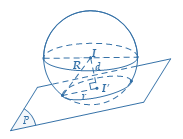
Mặt phẳng cắt mặt cầu theo thiết diện là đường tròn có tâm $I'$ và bán kính $r=\sqrt{{{R}^{2}}-I{{H}^{2}}}$ |
|
|
|
|
Lưu ý:
Khi mặt phẳng $\left( P \right)$ đi qua tâm $I$ của mặt cầu thì mặt phẳng $\left( P \right)$ được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.
3.3. Vị trí tương đối giữa mặt cầu và đường thẳng
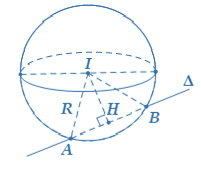
Cho mặt cầu $S\left( I;R \right)$ và đường thẳng $\Delta $. Gọi $H$ là hình chiếu của $I$ lên $\Delta $. Khi đó:
|
$IH>R$ |
$IH=R$ |
$IH<R$ |
|
$\Delta $ không cắt mặt cầu. |
$\Delta $ tiếp xúc với mặt cầu. $\Delta $: Tiếp tuyến của $\left( S \right)$ $H:$ tiếp điểm. |
$\Delta $ cắt mặt cầu tại hai điểm phân biệt. |
|
|
|
|
Lưu ý:
Trong trường hợp $\Delta $ cắt $\left( S \right)$ tại 2 điểm $A,B$ thì bán kính $R$ của $\left( S \right)$ được tính như sau: $\left\{ \begin{array}{l}
d\left( {I;\Delta } \right) = IH\\
R = \sqrt {I{H^2} + A{H^2}} = \sqrt {I{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}}
\end{array} \right.$
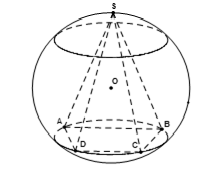
3.4. Đường kinh tuyến và vĩ tuyến của mặt cầu
|
Nội dung |
Hình vẽ |
|
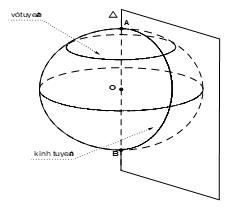
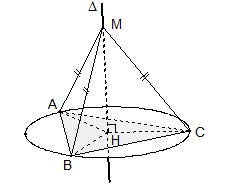
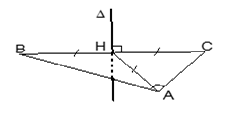
Giao tuyến của mặt cầu với nửa mặt phẳng có bờ là trục của mặt cầu được gọi là kinh tuyến. Giao tuyến (nếu có) của mặt cầu với các mặt phẳng vuông góc với trục được gọi là vĩ tuyến của mặt cầu. Hai giao điểm của mặt cầu với trục được gọi là hai cực của mặt cầu |
|
* Mặt cầu nội tiếp, ngoại tiếp hình đa diện:
|
Nội dung |
Hình vẽ |
|
Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện. Còn nói hình đa diện ngoại tiếp mặt cầu. |
|
|
Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu. Còn nói hình đa diện nội tiếp mặt cầu. Mặt cầu tâm $O$ bán kính $r$ ngoại tiếp hình chóp $S.ABCD$ khi và chỉ khi $OA=OB=OC=OD=OS=r$ |
|
Cho mặt cầu $S\left( I;R \right)$
- Diện tích mặt cầu: .$S=4\pi {{R}^{2}}$
- Thể tích khối cầu: $V=\frac{4}{3}\pi {{R}^{3}}$
4. MỘT SỐ DẠNG TOÁN VÀ CÔNG THỨC GIẢI
4.1. Bài toán mặt nón
4.1.1.Dạng 1. Thiết diện của hình nón cắt bởi một mặt phẳng
|
Nội dung |
Hình vẽ |
|
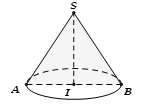
Thiết diện qua trục của hình nón là tam giác cân. |
|
|
Thiết diện qua đỉnh của hình nón là những tam giác cân có hai cạnh bên là hai đường sinh của hình nón. |
|
|
Thiết diện vuông góc với trục của hình nón là những đường tròn có tâm nằm trên trục của hình nón. |
|
4.1.2. Dạng 2. Bài toán liên quan đến thiết diện qua đỉnh của hình nón
Cho hình nón có chiều cao là h , bán kính đáy r và đường sinh l .
Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là d
|
Nội dung |
Hình vẽ |
|
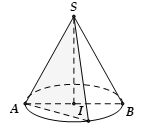
Gọi $M$ là trung điểm của $AC.$ Khi đó:
Diện tích thiết diện ${{S}_{td}}={{S}_{\Delta ABC}}=\frac{1}{2}SM.AC=\frac{1}{2}\sqrt{S{{I}^{2}}+I{{M}^{2}}}.2\sqrt{A{{I}^{2}}-I{{M}^{2}}}$ $=\sqrt{{{r}^{2}}-\frac{{{h}^{2}}{{d}^{2}}}{{{h}^{2}}-{{d}^{2}}}}.\sqrt{{{h}^{2}}+\frac{{{h}^{2}}{{d}^{2}}}{{{h}^{2}}-{{d}^{2}}}}$ |
|
4.1.3. Dạng 3. Bài toán hình nón ngoại tiếp và nội tiếp hình chóp
|
Nội dung |
Hình vẽ |
|
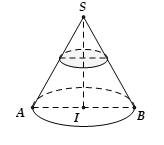
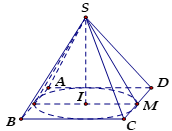
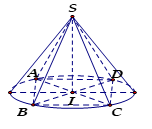
Hình nón nội tiếp hình chóp $S.ABCD$ đều là hình nón có đỉnh là $S$, đáy là đường tròn nội tiếp hình vuông $ABCD$. Khi đó hình nón có:
|
Hình chóp tứ giác đều S.ABCD
|
|
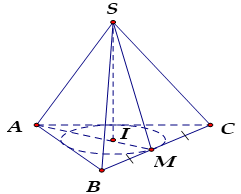
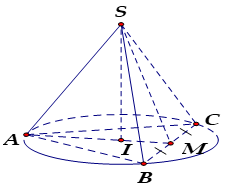
Hình nón ngoại tiếp hình chóp $S.ABCD$ đều là hình nón có đỉnh là $S$, đáy là đường tròn ngoại tiếp hình vuông $ABCD$. Khi đó hình nón có:
|
Hình chóp tứ giác đều S.ABCD
|
|
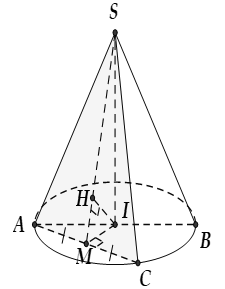
Hình nón nội tiếp hình chóp $S.ABC$ đều là hình nón có đỉnh là $S$, đáy là đường tròn nội tiếp tam giác $ABC$ Khi đó hình nón có
|
Hình chóp tam giác đều $S.ABC$
|
|
Hình nón ngoại tiếp hình chóp $S.ABC$ đều là hình nón có đỉnh là $S$, đáy là đường tròn ngoại tiếp tam giác $ABC$ Khi đó hình nón có:
Đường sinh: $l=SA$ |
Hình chóp tam giác đều $S.ABC$
|
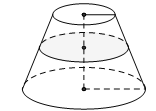
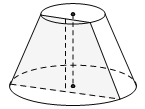
4.1.4. Dạng 4. Bài toán hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nón nằm giữa hai mặt phẳng nói trên được gọi là hình nón cụt.
|
Nội dung |
Hình vẽ |
|
Khi cắt hình nón cụt bởi một mặt phẳng song song với đáy thì được mặt cắt là một hình tròn. |
|
|
Khi cắt hình nón cụt bởi một mặt phẳng song song với trục thì được mặt cắt là một hình thang cân. |
|
|
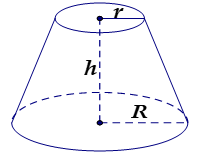
Cho hình nón cụt có $R,\ r,\ h$ lần lượt là bán kính đáy lớn, bán kính đáy nhỏ và chiều cao. Diện tích xung quanh của hình nón cụt: ${{S}_{xq}}=\pi l\left( R+r \right)$ Diện tích đáy (hình tròn): $S$đáy 1$=\pi {{r}^{2}}$; $S$đáy 2$=\pi {{r}^{2}}$$\Rightarrow \sum\limits_{{}}^{{}}{S}$đáy$=\pi \left( {{r}^{2}}+{{R}^{2}} \right)$ Diện tích toàn phần của hình nón cụt: ${{S}_{tp}}=\pi \lambda \left( R+r \right)+\pi {{r}^{2}}+\pi {{R}^{2}}$ Thể tích khối nón cụt: $V=\frac{1}{3}\pi h\left( {{R}^{2}}+{{r}^{2}}+Rr \right)$ |
|
4.1.5. Dạng 5. Bài toán hình nón tạo bởi phần còn lại của hình tròn sau khi cắt bỏ đi hình quạt
|
Nội dung |
Hình vẽ |
|
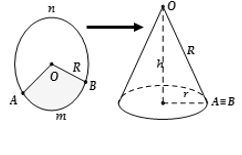
Từ hình tròn $\left( O;R \right)$ cắt bỏ đi hình quạt $AmB.$ Độ dài cung $\overset\frown{AnB}$ bằng $x.$ Phần còn lại của hình tròn ghép lại được một hình nón. Tìm bán kính, chiều cao và độ dài đường sinh của hình nón đó. Hình nón được tạo thành có $\left\{ \begin{array}{l} |
|
4.2. Một số dạng toán và công thức giải bài toán mặt trụ
4.2.1. Dạng 1. Thiết diện của hình trụ cắt bởi một mặt phẳng
|
Nội dung |
Hình vẽ |
|
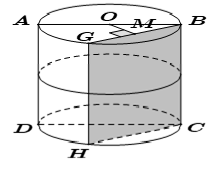
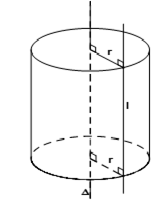
Thiết diện vuông góc trục là một đường tròn bán kính $R$ Thiết diện chứa trục là một hình chữ nhật $ABCD$ trong đó $AB=2R$ và $AD=h$. Nếu thiết diện qua trục là một hình vuông thì $h=2R$. Thiết diện song song với trục và không chứa trục là hình chữ nhật $BGHC$ có khoảng cách tới trục là: $d\left( OO';\left( BGHC \right) \right)=OM$ |
|
4.2.2. Dạng 2. Thể tích khối tứ diện có 2 cạnh là đường kính 2 đáy
|
Nội dung |
Hình vẽ |
|
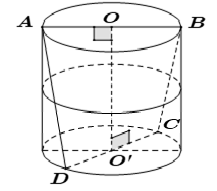
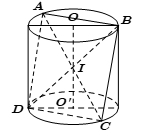
Nếu như $AB$ và $CD$ là hai đường kính bất kỳ trên hai đáy của hình trụ thì: ${{V}_{ABCD}}=\frac{1}{6}AB.CD.OO'.\sin \left( AB,CD \right)$ * Đặc biệt: Nếu $AB$ và $CD$ vuông góc nhau thì: ${{V}_{ABCD}}=\frac{1}{6}AB.CD.OO'$ |
|
4.2.3. Dạng 3. Xác định góc khoảng cách
|
Nội dung |
Hình vẽ |
|
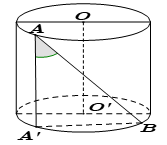
Góc giữa $AB$ và trục $OO'$: $\left( \widehat{AB,OO'} \right)=\widehat{A'AB}$ |
|
|
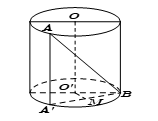
Khoảng cách giữa $AB$ và trục $OO'$: $d\left( AB;OO' \right)=OM$ |
|
|
Nếu $ABCD$ là một hình vuông nội tiếp trong hình trụ thì đường chéo của hình vuông cũng bằng đường chéo của hình trụ. Nghĩa là cạnh hình vuông: $AB\sqrt{2}=\sqrt{4{{R}^{2}}+{{h}^{2}}}$ |
|
4.2.4. Dạng 4. Xác định mối liên hệ giữa diện tích xung quanh, toàn phần và thể tích khối trụ trong bài toán tối ưu
|
Nội dung |
Hình vẽ |
|
Một khối trụ có thể tích $V$ không đổi.
${S_{tp\;\min }} \Leftrightarrow \left\{ \begin{array}{l}
${S_{\min }} \Leftrightarrow \left\{ \begin{array}{l} |
|
4.2.5. Dạng 5. Hình trụ ngoại tiếp, nội tiếp một hình lăng trụ đứng
Cho hình lăng trụ tam giác đêu nội tiếp trong một hình trụ. Thể tích khối lăng trụ là $V$ thì thể tích khối trụ là ${{V}_{\left( T \right)}}=\frac{4\pi V}{9}$
Cho hình lăng trụ tứ giác đêu $ABCD.A'B'C'D'$ ngoại tiếp trong một hình trụ. Diện tích xung quanh hình trụ là ${{S}_{xq}}$ thì diện tích xung quanh của hình lăng trụ là ${{S}_{aq}}=\frac{2S}{\pi }$
5. MỘT SỐ DẠNG TOÁN VÀ CÔNG THỨC GIẢI BÀI TOÁN MẶT CẦU
5.1. Mặt cầu ngoại tiếp khối đa diện
5.1.1. Các khái niệm cơ bản
Trục của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy  Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
 Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
 Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
5.1.2. Tâm và bán kính mặt cầu ngoại tiếp hình chóp
Tâm mặt cầu ngoại tiếp hình chóp: là điểm cách đều các đỉnh của hình chóp. Hay nói cách khác, nó chính là giao điểm $I$ của trục đường tròn ngoại tiếp mặt phẳng đáy và mặt phẳng trung trực của một cạnh bên hình chóp.
Bán kính: là khoảng cách từ $I$ đến các đỉnh của hình chóp.
5.1.3. Cách xác định tâm và bán kính mặt cầu của một số hình đa diện
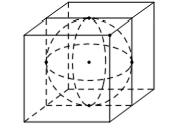
5.1.3.1. Hình hộp chữ nhật, hình lập phương
|
Nội dung |
Hình vẽ |
|
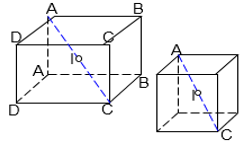
Tâm: trùng với tâm đối xứng của hình hộp chữ nhật (hình lập phương) $\Rightarrow $ Tâm là $I$, là trung điểm của $AC'$. Bán kính: bằng nửa độ dài đường chéo hình hộp chữ nhật (hình lập phương). $\Rightarrow $Bán kính: $R=\frac{AC'}{2}$ |
|
5.1.3.2. Hình lăng trụ đứng có đáy nội tiếp đường tròn
|
Nội dung |
Hình vẽ |
|
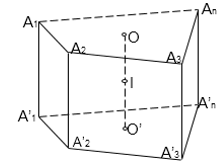
Xét hình lăng trụ đứng ${{A}_{1}}{{A}_{2}}{{A}_{3}}...{{A}_{n}}.A_{1}^{'}A_{2}^{'}A_{3}^{'}...A_{n}^{'}$, trong đó có 2 đáy ${{A}_{1}}{{A}_{2}}{{A}_{3}}...{{A}_{n}}$ và $A_{1}^{'}A_{2}^{'}A_{3}^{'}...A_{n}^{'}$ nội tiếp đường tròn $\left( O \right)$ và $\left( O' \right)$. Lúc đó, mặt cầu nội tiếp hình lăng trụ đứng có:
|
|
5.1.3.3. Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông
|
Nội dung |
Hình vẽ |
|
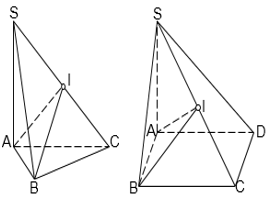
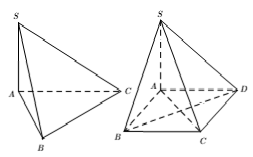
Hình chóp $S.ABC$ có $\widehat{SAC}=\widehat{SBC}={{90}^{0}}$.
Hình chóp $S.ABCD$ có $\widehat{SAC}=\widehat{SBC}=\widehat{SDC}={{90}^{0}}$.
|
|
5.1.3.4. Hình chóp đều
|
Nội dung |
Hình vẽ |
|
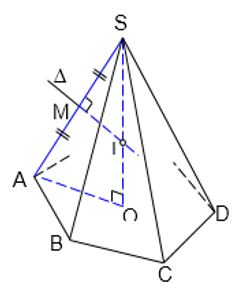
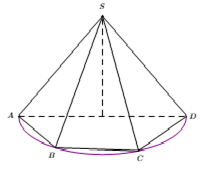
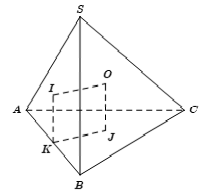
Cho hình chóp đều $S.ABC...$
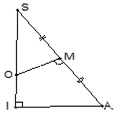
Bán kính: Ta có: $\Delta SMI\backsim \Delta SOA\Rightarrow \frac{SM}{SO}=\frac{SI}{SA}\Rightarrow $ Bán kính: $R=IS=\frac{SM.SA}{SO}=\frac{S{{A}^{2}}}{2SO}=IA=IB=IC=...$ |
|
5.1.3.5. Hình chóp có cạnh bên vuông góc với mặt phẳng đáy
|
Nội dung |
Hình vẽ |
|
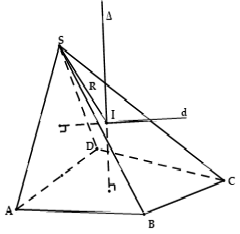
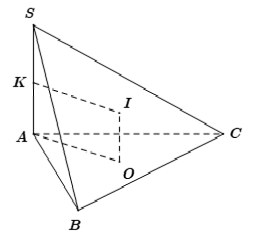
Cho hình chóp $S.ABC...$ có cạnh bên $SA\bot \left( ABC... \right)$ và đáy $ABC...$ nội tiếp được trong đường tròn tâm $O$. Tâm và bán kính mặt cầu ngoại tiếp hình chóp $S.ABC...$được xác định như sau:
$R=IA=IB=IC=IS=...$
Ta có: $MIOB$là hình chữ nhật. Xét $\Delta MAI$ vuông tại $M$ có: $R=AI=\sqrt{M{{I}^{2}}+M{{A}^{2}}}=\sqrt{A{{O}^{2}}+{{\left( \frac{SA}{2} \right)}^{2}}}$ |
|
5.1.3.6. Hình chóp khác

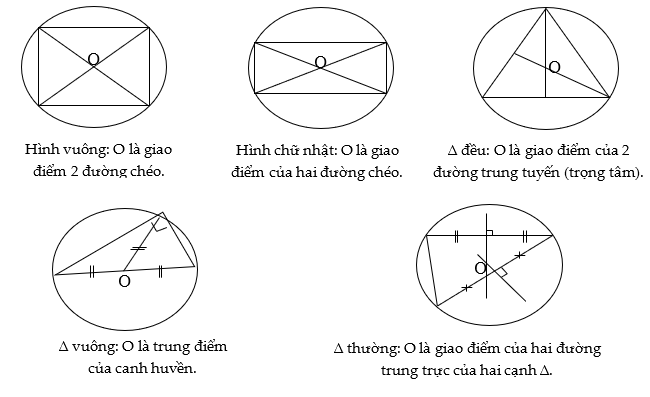
5.1.3.7. Đường tròn ngoại tiếp một số đa giác thường gặp
Khi xác định tâm mặt cầu, ta cần xác định trục của mặt phẳng đáy, đó chính là đường thẳng vuông góc với mặt phẳng đáy tại tâm O của đường tròn ngoại tiếp đáy. Do đó, việc xác định tâm ngoại O là yếu tố rất quan trọng của bài toán.
5.2. Kỹ thuật xác định mặt cầu ngoại tiếp hình chóp
|
Nội dung |
Hình vẽ |
|
Cho hình chóp $S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ (thoả mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng $\Delta $: trục đường tròn ngoại tiếp đa giác đáy.
Lập mặt phẳng trung trực $\left( \alpha \right)$ của một cạnh bên. Lúc đó
|
|
5.3. Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy
5.3.1. Trục đường tròn ngoại tiếp đa giác đáy
|
Nội dung |
Hình vẽ |
|
Định nghĩa Trục đường tròn ngoại tiếp đa giác đáy là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với mặt phẳng đáy. Tính chất $\forall M\in \Delta :\ MA=MB=MC$ Suy ra: $MA=MB=MC\Leftrightarrow M\in \Delta $ Các bước xác định trục
Xác định tâm $H$ của đường tròn ngoại tiếp đa giác đáy.
Qua $H$ dựng $\Delta $ vuông góc với mặt phẳng đáy. Một số trường hợp đặc biệt
|
|
5.3.2. Kỹ năng tam giác đồng dạng
|
Nội dung |
Hình vẽ |
|
$\Delta SMO$ đồng dạng với $\Delta SIA\Rightarrow \frac{SO}{SA}=\frac{SM}{SI}$ |
|
5.3.3. Nhận xét quan trọng
$\exists M,S:\;\left\{ \begin{array}{l}
MA = MB = MC\\
SA = SB = SC
\end{array} \right. \Rightarrow SM$ là trục đường tròn ngoại tiếp $\Delta ABC$.
5.4. Kỹ thuật sử dụng hai trục xác định tâm mặt cầu ngoại tiếp đa diện
|
Nội dung |
Hình vẽ |
|
Cho hình chóp $S.{{A}_{1}}{{A}_{2}}{{A}_{3}}...{{A}_{n}}$ (thõa mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng $\Delta $: trục đường tròn ngoại tiếp đa giác đáy.
Xác định trục $d$ của đường tròn ngoại tiếp một mặt bên (dễ xác định) của khối chóp. Lúc đó:
|
|
5.5. Tổng kết các dạng tìm tâm và bán kính mặt cầu
5.5.1. Dạng 1
|
Nội dung |
Hình vẽ |
|
Cạnh bên SA vuông góc đáy và $\widehat{ABC}={{90}^{0}}$ khi đó $R=\frac{SC}{2}$ và tâm là trung điểm $SC$. |
|
5.5.2. Dạng 2
|
Nội dung |
Hình vẽ |
|
Cạnh bên $SA$ vuông góc đáy và bất kể đáy là hình gì, chỉ cần tìm được bán kính đường tròn ngoại tiếp của đáy là ${{R}_{D}}$, khi đó : ${{R}^{2}}=R_{D}^{2}+\frac{S{{A}^{2}}}{4}$
|
|
5.5.3. Dạng 3
|
Nội dung |
Hình vẽ |
|
Chóp có các cạnh bên bằng nhau: $SA=SB=SC=SD$ : $R=\frac{S{{A}^{2}}}{2SO}$
|
|
5.5.4. Dạng 4
|
Nội dung |
Hình vẽ |
|
Hai mặt phẳng $\left( SAB \right)$ và $\left( ABC \right)$ vuông góc với nhau và có giao tuyến $AB$. Khi đó ta gọi ${{R}_{1}},{{R}_{2}}$ lần lượt là bán kính đường tròn ngoại tiếp các tam giác $SAB$ và $ABC$. Bán kính mặt cầu ngoại tiếp: ${{R}^{2}}={{R}_{1}}^{2}+{{R}_{2}}^{2}-\frac{A{{B}^{2}}}{4}$ |
|
5.5.5. Dạng 5
Chóp $S.ABCD$ có đường cao $SH$, tâm đường tròn ngoại tiếp đáy là $O$. Khi đó ta giải phương trình: ${{\left( SH-x \right)}^{2}}+O{{H}^{2}}={{x}^{2}}+R_{D}^{2}$ . Với giá trị $x$ tìm được ta có: ${{R}^{2}}={{x}^{2}}+R_{D}^{2}$
5.5.6. Dạng 6: Bán kính mặt cầu nội tiếp: $r=\frac{3V}{{{S}_{tp}}}$
6. TỔNG HỢP CÁC CÔNG THỨC ĐẶC BIỆT VỀ KHỐI TRÒN XOAY
6.1. Chỏm cầu
|
Nội dung |
Hình vẽ |
| $\left\{ \begin{array}{l} {S_{xq}} = 2\pi Rh = \pi \left( {{r^2} + {h^2}} \right)\\ V = \pi {h^2}\left( {R - \frac{h}{3}} \right) = \frac{{\pi h}}{6}\left( {{h^2} + 3{r^2}} \right) \end{array} \right.$ |
|
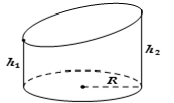
6.2. Hình trụ cụt
|
Nội dung |
Hình vẽ |
|
$\left\{ \begin{array}{l} |
|
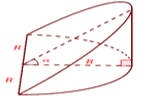
6.3. Hình nêm loại 1
|
Nội dung |
Hình vẽ |
|
$V=\frac{2}{3}{{R}^{3}}\tan \alpha $ |
|
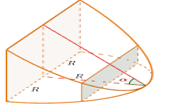
6.4. Hình nêm loại 2
|
Nội dung |
Hình vẽ |
|
$V=\left( \frac{\pi }{2}-\frac{2}{3} \right){{R}^{3}}\tan \alpha $ |
|
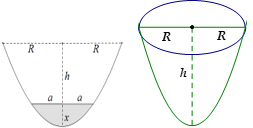
6.5. Parabol bậc hai-Paraboloid tròn xoay
|
Nội dung |
Hình vẽ |
| $\left\{ \begin{array}{l} {S_{parabol}} = \frac{4}{3}Rh;\;\frac{{S'}}{S} = {\left( {\sqrt {\frac{x}{h}} } \right)^3} = {\left( {\frac{a}{r}} \right)^3}\\ v = \frac{1}{2}\pi {R^2}h = \frac{1}{2}{V_{tru}} \end{array} \right.$ |
|
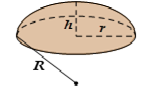
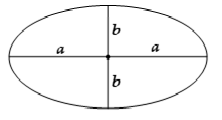
6.6. Diện tích Elip và Thể tích khối tròn xoay sinh bởi Elip
|
Nội dung |
Hình vẽ |
| $\left\{ \begin{array}{l} {S_{elip}} = \pi ab\\ {V_{xoay\;quanh\;2a}} = \frac{4}{3}\pi a{b^2}\\ {V_{xoay\;quanh\;2b}} = \frac{4}{3}\pi {a^2}b \end{array} \right.$ |
|
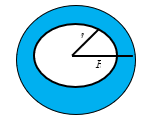
6.7. Diện tích hình vành khăn
|
Nội dung |
Hình vẽ |
|
$S=\pi \left( {{R}^{2}}-{{r}^{2}} \right)$ |
|
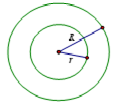
6.8. Thể tích hình xuyến (phao)
|
Nội dung |
Hình vẽ |
|
$V=2{{\pi }^{2}}\left( \frac{R+r}{2} \right){{\left( \frac{R-r}{2} \right)}^{2}}$ |
|