Diện tích tam giác là một trong những công thức toán học mà bạn sẽ được học và áp dụng rất nhiều trong các bài tập của môn Toán học. Để tính được diện tích hình tam giác, có rất nhiều công thức và cách áp dụng khác nhau. Muốn tăng khả năng tư duy và tính toán diện tích hình tam giác thì đừng bỏ qua bài viết này.
Dưới đây, The Dewey Schools sẽ tổng hợp các công thức tính diện tích tam giác đầy đủ nhất.
Trước khi đi vào tính diện tích tam giác, chúng ta cần hiểu hơn về định nghĩa hình tam giác và ghi nhớ những tính chất đặc biệt của hình tam giác.
Định nghĩa
Hình tam giác là một hình học cơ bản trong toán học và hình học. Nó là một đa giác có ba cạnh và ba đỉnh. Các cạnh của tam giác nối các đỉnh với nhau và các góc giữa các cạnh tạo thành các góc của tam giác.

Hình tam giác là gì
Phân loại
Có một số cách phân loại tam giác dựa trên các tính chất khác nhau của nó:
1. Theo cạnh
- Tam giác đều: Có ba cạnh bằng nhau và ba góc bằng nhau (60 độ).
- Tam giác cân: Có ít nhất hai cạnh bằng nhau.
- Tam giác vuông: Có một góc vuông (90 độ).
2. Theo góc
- Tam giác nhọn: Có ba góc nhọn, tức là các góc đều nhỏ hơn 90 độ.
- Tam giác tù: Có một góc tù, tức là một góc lớn hơn 90 độ.
- Tam giác vuông: Đã đề cập ở trên, có một góc vuông.
3, Theo độ dài các cạnh
- Tam giác thường: Có ba cạnh và ba góc đều không bằng nhau.
- Tam giác đều, cân, vuông, tù…
>>Xem thêm: Học môn tự nhiên nên thi khối nào? Các ngành học triển vọng năm 2023
Tính chất
Hình tam giác có nhiều tính chất quan trọng và đáng chú ý trong hình học và toán học. Dưới đây là một số tính chất cơ bản của tam giác, hãy ghi nhớ để làm bài tập một cách hiệu quả:
- Tổng các góc trong tam giác: Tổng của ba góc trong một tam giác luôn bằng 180 độ. Công thức này được gọi là Định lý tổng các góc trong tam giác.
- Định lý góc ngoài tam giác: Mỗi góc ngoài của tam giác bằng tổng hai góc trong tam giác không chứa nó. Hay nói cách khác, mỗi góc ngoài bằng góc phần còn lại khi ta loại bỏ nó khỏi tam giác.
- Bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại. Nếu tam giác có cạnh đủ dài, tổng hai cạnh ngắn hơn sẽ lớn hơn cạnh dài nhất.
- Định lý Pythagoras: Đối với tam giác vuông, bình phương độ dài cạnh huyền (cạnh đối diện góc vuông) bằng tổng bình phương độ dài hai cạnh góc vuông (được gọi là định lý Pythagoras).
- Đoạn phân giác của tam giác: Đoạn thẳng từ một đỉnh của tam giác đến điểm trên cạnh đối diện, sao cho chia cạnh thành hai đoạn có tỷ số bằng tỷ số độ dài hai cạnh còn lại, đó là đoạn phân giác.
- Các trung điểm trong tam giác: Ba đoạn thẳng nối các đỉnh của tam giác tới các điểm trung điểm của cạnh đối diện là ba đoạn thẳng có độ dài bằng nhau và giao nhau tại một điểm (gọi là trọng tâm của tam giác).
- Tính chất chu vi và diện tích: Tam giác có chu vi bằng tổng độ dài ba cạnh của nó. Diện tích của tam giác có thể được tính bằng nhiều phương pháp khác nhau như Công thức diện tích Heron hoặc sử dụng chiều cao và cạnh tương ứng.
Đây chỉ là một số tính chất cơ bản của tam giác. Tam giác là một hình học đa diện đa dạng, có nhiều tính chất khác nhau và được nghiên cứu sâu trong hình học và các lĩnh vực toán học liên quan.
Tổng hợp 6 công thức tính diện tích tam giác chi tiết
Để tính diện tích tam giác, dựa vào đặc điểm phân loại của tam giác đó có thể áp dụng được nhiều công thực tính khác nhau. Dưới đây là tổng hợp 6 công thức tính diện tích hình tam giác chi tiết:

Tổng hợp 6 công thức tính diện tích tam giác chi tiết
Cách tính diện tích tam giác thường abc chính xác
Tam giác thường là tam giác có độ dài các cạnh khác nhau và số đo 3 góc cũng khác nhau.
Công thức tính S tam giác thường abc được tính như sau: Độ dài của một cạnh bất kỳ nhân với chiều cao tương ứng của cạnh đó và chia 2.

Cách tính diện tích tam giác thường abc chính xác
Trong đó:
- a là độ dài của một cạnh bất kỳ
- h là chiều cao hạ từ đỉnh tam giác xuống cạnh a đó
Ví dụ: Tam giác ABC có độ dài cạnh a là 6cm, chiều cao h hạ từ đỉnh xuống cạnh A có độ dài là 4 cm. Vậy diện tích tam giác ABC được tính như sau: ½ (6*4) = 12 cm²
Kiến thức nâng cao: Để tính diện tích tam giác thường abc, dựa trên những thông tin có sẵn, bạn có thể áp dụng một số công thức nâng cao sau:
- Sử dụng công thức diện tích Heron
Đối với tam giác ABC có ba cạnh a, b và c, và nửa chu vi là p (p = (a + b + c) / 2), diện tích tam giác được tính bằng công thức Heron:
S(ABC) = √(p * (p – a) * (p – b) * (p – c))
- Sử dụng định lý Sine
Nếu bạn biết một góc và hai cạnh trong tam giác ABC, bạn có thể sử dụng định lý Sine để tính diện tích. Định lý Sine cho biết:
S(ABC) = (1/2) * a * b * sin(C)
Trong đó C là góc giữa hai cạnh a và b
Cách tính S tam giác vuông kèm ví dụ
Tam giác vuông là tam giác có một góc vuông. Góc vuông là góc mà hai cạnh tạo thành nó vuông góc với nhau, có nghĩa là chúng gặp nhau sao cho điểm giao của chúng tạo thành một góc vuông 90 độ.
Công thức tính diện tích tam giác vuông như sau: Độ dài hai cạnh góc vuông nhân với nhau và chia cho 2
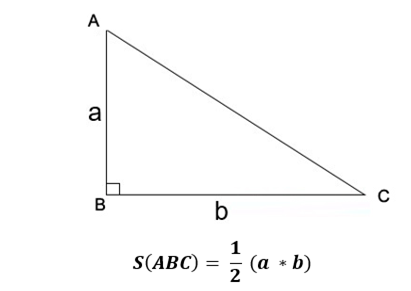
Trong đó: a, b là độ dài của hai cạnh góc vuông
Ví dụ: Tam giác vuông ABC có độ dài 2 cạnh góc vuông lần lượt là 5 cm và 8 cm. Diện tích tam giác ABC lúc này được tính như sau: ½ (5 * 8) = 20 cm²
Công thức diện tích tam giác vuông cân đầy đủ
Tam giác vuông cân là một loại hình tam giác vuông đặc biệt, có hai cạnh có độ dài bằng nhau, tạo thành góc vuông, và đồng thời cũng là hai cạnh góc vuông
Công thức tính diện tích tam giác vuông cân được tính như sau: Độ dài của một cạnh góc vuông bình phương sau đó chia 2.
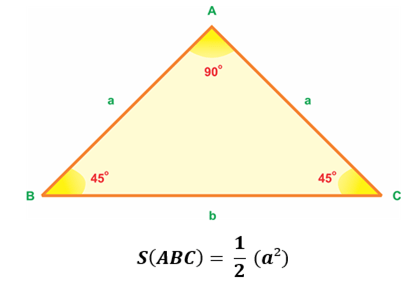
Công thức diện tích tam giác vuông cân đầy đủ
Trong đó: a là độ dài hai cạnh góc vuông bằng nhau.
Ví dụ: Tam giác vuông cân ABC có độ dài hai cạnh góc vuông là 4 cm. Diện tích tam giác ABC được tính như sau: S(ABC) = ½ (4²) = 8 cm²
Cách tính diện tích tam giác cân đơn giản
Tam giác cân là một loại hình tam giác đặc biệt, có hai cạnh có độ dài bằng nhau và hai góc đối diện với những cạnh này cũng bằng nhau.
Công thức tính diện tích tam giác cân được tính như sau: Độ dài cạnh còn lại nhân với chiều cao tương ứng của cạnh đó rồi chia 2.
Trong đó:
- a là chiều dài cạnh còn lại khác 2 cạnh có độ dài bằng nhau (BC)
- h là chiều cao nối từ đỉnh góc đối diện của cạnh đó xuống đáy (AM)
Ví dụ: Cho tam giác cân ABC có độ dài 2 cạnh AB và AC bằng nhau, cạnh BC có độ dài là 9 cm. Chiều cao nối từ đỉnh A xuống BC có độ dài là 5 cm. Diện tích tam giác ABC cân được tính như sau: S(ABC) = ½ (9 * 5) = 22,5 cm²
Công thức tính diện tích tam giác đều cạnh a
Tam giác đều là một loại hình tam giác đặc biệt, có ba cạnh và ba góc đều nhau. Tức là tất cả các cạnh của tam giác đều có độ dài bằng nhau và tất cả các góc của tam giác đều có độ lớn chính xác là 60 độ.
Công thức tính diện tích tam giác đều cạnh a được tính như sau: Độ dài của một cạnh bất kỳ nhân với chiều cao bất kỳ và chia 2.
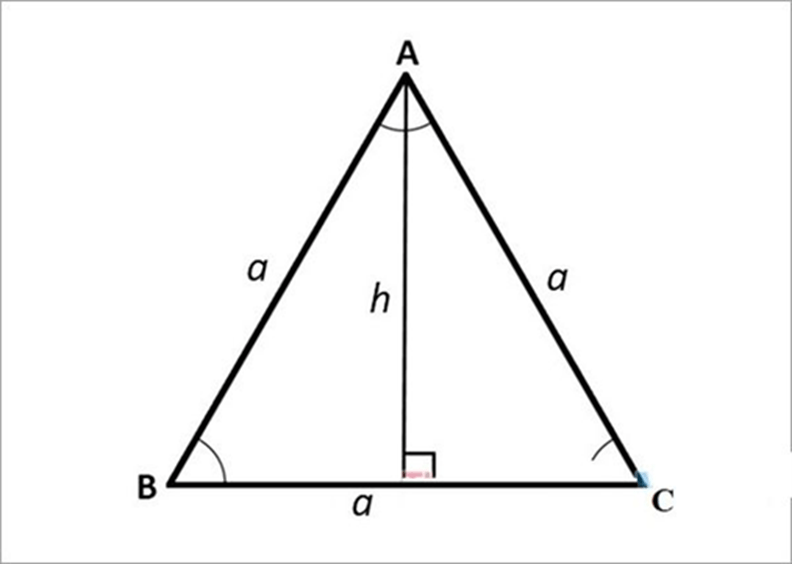
Công thức tính diện tích tam giác đều cạnh a
Trong đó:
- a là chiều dài của một cạnh bất kỳ
- h là chiều cao bất kỳ (trong tam giác đều, chiều cao của các cạnh đều bằng nhau)
Ví dụ: Tam giác đều ABC có các cạnh bằng nhau và bằng 7cm, chiều cao hạ từ đỉnh A xuống cạnh BC là 6 cm. Diện tích tam giác ABC được tính như sau:
S(ABC) = ½ (7 * 6) = 21 cm²
Công thức tính diện tích tam giác trong Oxyz
Trong hệ tọa độ Oxyz, tam giác là một đa giác ba cạnh nằm trong không gian ba chiều, được xác định bởi ba điểm không cùng một đường thẳng. Các điểm đó được biểu diễn bằng các tọa độ (x, y, z), trong đó x, y và z là các số thực thể hiện vị trí của điểm trong không gian.
Công thức tính diện tích tam giác trong hệ trục tọa độ Oxyz được tính như sau: Diện tích tam giác ABC được tính bằng nửa giá trị tuyệt đối của tích hạng ba của hai vectơ AB và AC:
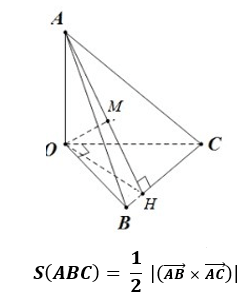
Trong đó: AB và AC là hai vectơ được biểu diễn trên trục Oxyz
Ví dụ: Trên hệ trục tọa độ cho tam giác ABC có 3 điểm A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). Diện tích tam giác ABC được tính như sau:
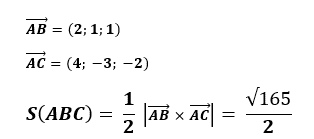
Các dạng bài tập tính diện tích tam giác thường gặp
Từ công thức tính diện tích tam giác sẽ có rất nhiều dạng bài tập mà bạn cần lưu ý vì sẽ thường xuyên gặp trong nhiều bài tập. Ghi nhớ những công thức ở trên và tìm hiểu các dạng bài tập dưới đây sẽ giúp bé có thể nhanh chóng giải quyết các bài tập:
Bài tập tính S tam giác khi biết chiều dài cạnh đáy và chiều cao h
Đây là dạng bài tập khá dễ, áp dụng công thức tính diện tích tam giác cơ bản là sẽ cho ra kết quả chính xác: :
S (ABC) = ½ (a*h).
Bài tập minh họa: Cho tam giác ABC có độ dài cạnh BC là 40 cm, chiều cao tương ứng với cạnh đáy BC có độ dài là 5 cm. Tính diện tích tam giác ABC
Lời giải: S(ABC) = ½ (BC * h) = ½ (40 * 5) = 100 cm²
Bài tập tính S tam giác khi biết độ dài các cạnh
Với dạng bài tập này, ta có thể giải theo cách là áp dụng công thức Heron:
S(ABC) = √(p * (p – a) * (p – b) * (p – c))
Trong đó, tam giác ABC có ba cạnh a, b và c, và nửa chu vi là p (p = (a + b + c) / 2)
Bài tập tính S tam giác đều khi biết độ dài một cạnh

Khi biết độ dài một cạnh trong tam giác đều, đồng nghĩa với việc ta biết độ dài của cả ba cạnh và biết 3 góc bằng nhau và bằng 60 độ. Đối với dạng bài tập này có thể tính theo 3 cách như sau:
- Cách 1: Áp dụng công thức Heron
- Cách 2: Định lý Cosine, diện tích tam giác sẽ là: S(ABC) = (1/2) * a² * sin(60⁰).
- Cách 3: Đi tìm chiều cao của tam giác. Lúc này, chiều cao sẽ được tính theo công thức như sau: h = a² – (a/2)² . Sau khi tính được h, áp dụng công thức tính diện tích như bình thường là ra.
Bài tập tính diện tích tam giác trong tọa độ Oxyz
Trong hệ tọa độ Oxyz, cho 3 điểm
- A (x1; y1; z1)
- B (x2; y2; z2)
- C (x3; y3; z3)
Dựa trên công thức:
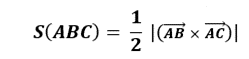
Ta tìm được 2 vecto AB và AC bằng cách trừ các điểm x;y;z của 2 điểm A với B và A với C
Sau khi tìm được tọa độ (x; y; z) của 2 vecto đó ta tiến hành nhân 2 vecto lại với nhau và chia cho 2 là ra kết quả.
Tìm độ dài cạnh huyền trong tam giác vuông khi biết diện tích và cạnh a
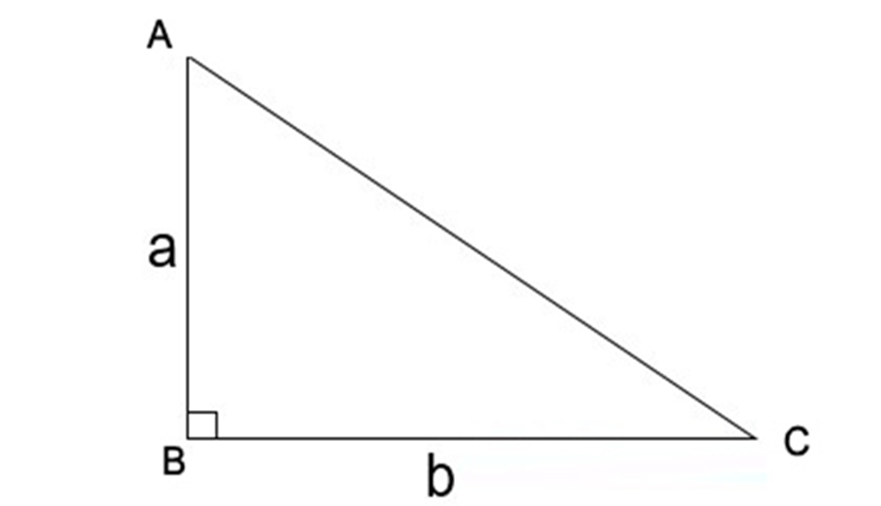
Công thức tính diện tích tam giác vuông như sau: S (ABC) = ½ (a * b).
Để tìm được độ dài cạnh huyền, ta tiến hành các bước như sau:
- Tìm độ dài cạnh b = (S(ABC) * 2) / a
- Sau khi biết độ dài cạnh b, ta áp dụng công thức Pytago: c² = a² + b²
- Tìm được c² ta sẽ có kết quả của c là cạnh huyền của tam giác vuông ABC
Tìm S tam giác khi biết chu vi và bán kính đường tròn nội tiếp
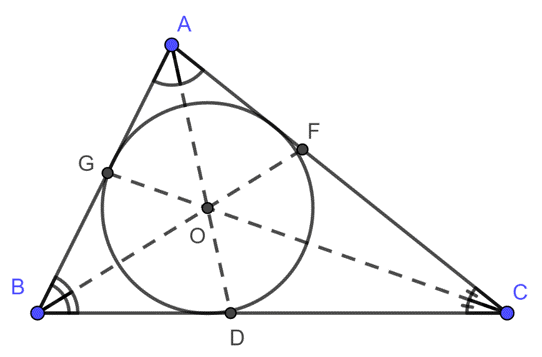
Để tính diện tích tam giác khi biết chu vi (P) và bán kính đường tròn nội tiếp (r), ta sử dụng một công thức liên quan đến tam giác và đường tròn nội tiếp.
Đặt a, b và c lần lượt là ba cạnh của tam giác và R là bán kính đường tròn ngoại tiếp tam giác (được tính bằng ba đỉnh của tam giác). Ta có các mối quan hệ sau:
- Diện tích tam giác (S) và bán kính đường tròn ngoại tiếp (R):
S = (abc) / (4R)
- Diện tích tam giác (S) và chu vi (P):
S = (P * r) / 2
Trong đó, P là chu vi tam giác và r là bán kính đường tròn nội tiếp tam giác.
Bây giờ, chúng ta có thể giải hai công thức này để tìm diện tích tam giác (S):
Từ công thức (1):
(P * r) / 2 = (abc) / (4R)
Từ công thức (2):
S = (P * r) / 2
Kết hợp hai công thức trên:
S = ((abc) / (4R)) / 2
S = (abc) / (8R)
Vì vậy, diện tích tam giác (S) có thể được tính bằng công thức S = (abc) / (8R), khi biết chu vi (P) và bán kính đường tròn nội tiếp (r) của tam giác.
Một số bài tập tính diện tích tam giác điển hình kèm lời giải chi tiết
Dựa vào công thức và các dạng bài tập trên, bạn đã nắm được cách tính diện tích tam giác khi áp dụng vào bài tập cụ thể. Nếu như vẫn còn khó hình dung về cách làm bài hiệu quả, bạn hãy tham khảo một số bài tập điển hình từ cơ bản đến nâng cao dưới đây nhé!
Bài tập 1
Tam giác ABC là tam giác vuông tại A, có chiều cao h = 6 cm. Độ dài cạnh góc vuông là 8 cm. Tính diện tích của tam giác ABC.
Lời giải:
Vì tam giác ABC là tam giác vuông tại A, ta biết cạnh góc vuông có độ dài 8 cm và chiều cao h = 6 cm.
Tính diện tích tam giác (S) bằng cách sử dụng công thức diện tích tam giác: S = (1/2) * cạnh góc vuông * chiều cao.
S = (1/2) * 8 cm * 6 cm = 24 cm²
Vậy diện tích của tam giác ABC là 24 cm².
Bài tập 3
Tam giác vuông ABC có cạnh góc vuông AB có độ dài 10 cm và diện tích S = 40 cm². Tính độ dài cạnh huyền BC của tam giác vuông ABC.
Lời giải:
Ta biết tam giác vuông ABC có cạnh góc vuông AB có độ dài 10 cm và diện tích S = 40 cm².
Bước 1: Tính độ dài cạnh góc vuông còn lại AC = (S * 2)/ AB = (40 * 2)/10 = 8 cm
Bước 2: Tính độ dài cạnh huyền BC của tam giác vuông.Dựa vào công thức Pytago ta có bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông
Do đó (BC)².= (AB)². + (AC)². = 10². + 8². = 164
>> BC = √164 = xấp xỉ 12,9 cm
Bài tập 4
Tam giác ABC có độ dài ba cạnh là: AB = 6 cm, BC = 8 cm và AC = 10 cm. Tính diện tích của tam giác ABC.
Lời giải:
Để tính diện tích tam giác khi biết độ dài ba cạnh, chúng ta sử dụng công thức Heron. Công thức này được dùng để tính diện tích của tam giác khi biết độ dài ba cạnh.
Công thức Heron:
Diện tích tam giác ABC (S) = √(p * (p – a) * (p – b) * (p – c))
Trong đó:
a, b và c là độ dài ba cạnh của tam giác (trong trường hợp này, a = 6 cm, b = 8 cm và c = 10 cm).
p là nửa chu vi của tam giác, được tính bằng p = (a + b + c) / 2.
Bước 1: Tính nửa chu vi p của tam giác.
p = (6 cm + 8 cm + 10 cm) / 2 = 24 cm / 2 = 12 cm
Bước 2: Tính diện tích tam giác (S) bằng công thức Heron.
S = √(12 cm * (12 cm – 6 cm) * (12 cm – 8 cm) * (12 cm – 10 cm))
S = √(12 cm * 6 cm * 4 cm * 2 cm) = √(576 cm²) = 24 cm²
Vậy diện tích của tam giác ABC là 24 cm².
Bài tập 4
Tam giác ABC có chu vi P = 30 cm và bán kính đường tròn nội tiếp R = 5 cm. Tính diện tích của tam giác ABC.
Lời giải:
Để tính diện tích tam giác khi biết chu vi và bán kính đường tròn nội tiếp, chúng ta sử dụng một công thức liên quan đến tam giác và đường tròn nội tiếp.
Cho tam giác ABC có chu vi P và bán kính đường tròn nội tiếp R, ta có các mối quan hệ sau:
- Diện tích tam giác (S) và bán kính đường tròn ngoại tiếp (R):
S = (P * R) / 2
- Diện tích tam giác (S) và chu vi (P):
S = (P * R) / 2
Trong đó, P là chu vi tam giác và R là bán kính đường tròn nội tiếp tam giác.
Bước 1: Tính diện tích tam giác (S) bằng công thức diện tích tam giác và chu vi tam giác.
S = (P * R) / 2 = (30 cm * 5 cm) / 2 = 150 cm² / 2 = 75 cm²
Vậy diện tích của tam giác ABC là 75 cm².
Câu hỏi thường gặp
Cách tính diện tích tam giác lớp 5
Ngay từ lớp 5, chúng ta đã được học cách tính diện tích tam giác thường ABC. Công thức tính diện tích tam giác lớp 5 đó là: S(ABC) = ½ (a * h).
Trong đó, a là độ dài của một cạnh trong tam giác, h là chiều cao tương ứng của cạnh a
Với công thức này, ta có thể áp dụng hầu hết đối với các hình tam giác đặc biệt như tam giác cân, tam giác đều, tam giác vuông,…
Tính diện tích tam giác biết 3 cạnh
Cách tính diện tích tam giác khi biết độ dài 3 cạnh cũng đã được đề cập ở trên. Để tính diện tích trong trường hợp này, ta không thể áp dụng công thức cơ bản như bình thường nữa mà phải sử dụng công thức Heron S(ABC) = √(p * (p – a) * (p – b) * (p – c))
Trong đó, a, b, c là độ dài các cạnh đã cho trước, p là chu vi của tam giác được tính theo công thức p = a+b+c
Trên đây là toàn bộ kiến thức về diện tích tam giác mà TDS đã tổng hợp lại. Có thể thấy rằng diện tích hình tam giác có nhiều công thức tính rất hay và đa dạng. Để học toán tốt hơn, bạn đừng quên lưu lại những công thức trên và thường xuyên làm bài tập áp dụng cách tính để đạt kết quả cao nhé! Chúc bạn có những giờ học toán đầy hứng thú và bổ ích.
—-
The Dewey Schools là hệ thống trường quốc tế song ngữ tốt nhất hiện nay tại Hà Nội, tiên phong mang đến nền giáo dục chuẩn Mỹ và thế giới tại Việt Nam. Được thành lập từ năm 2011, đến nay Dewey Schools đã có cho mình hơn 8000 học sinh, 1600 cán bộ nhân viên, 4 cơ sở trường tại Hà Nội và Hải Phòng. Ngoài cơ sở vật chất hiện đại bậc nhất, Dewey Schools còn ghi điểm trong mắt phụ huynh bởi chất lượng đào tạo và triết lý giáo dục nổi bật giúp học sinh có được hành trang tốt nhất để bước vào đời.
Thông tin cơ bản:
- Hotline: 19003293
- Website: https://cuongthinhcorp.com.vn/
- Học phí The Dewey Schools