Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cùng khám phá | SGK Toán 11 - Cùng khám phá

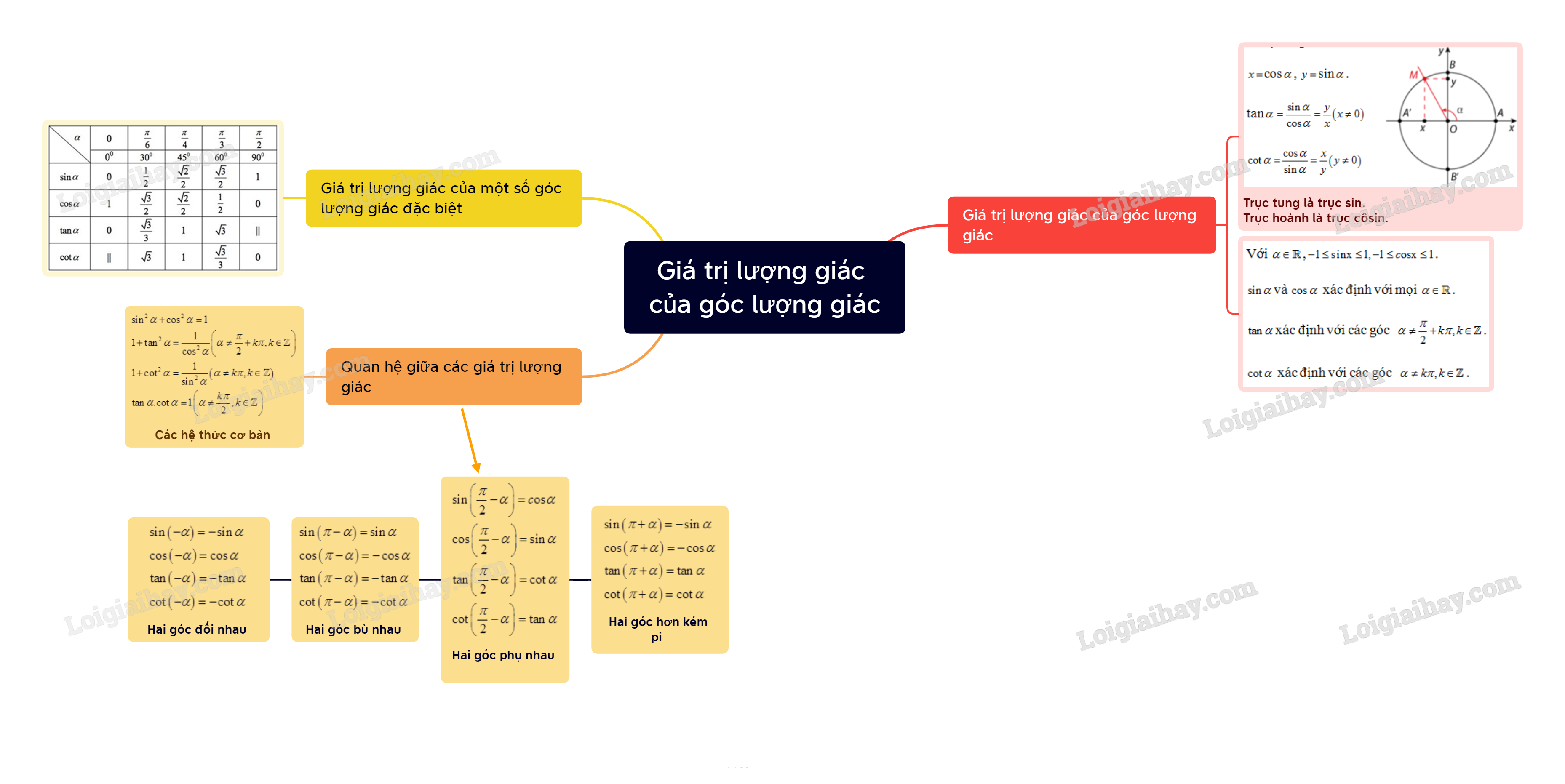
I. Giá trị lượng giác của góc lượng giác

1. Định nghĩa

Bạn đang xem: Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cùng khám phá | SGK Toán 11 - Cùng khám phá

 

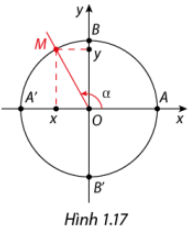
- Trên đàng tròn trặn, lấy điểm M(x;y) như hình vẽ. Khi đó:

\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).

tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)

\(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)

- Các độ quý hiếm sin\(\alpha \), cos\(\alpha \), tan\(\alpha \), cot\(\alpha \) được gọi là những độ quý hiếm lượng giác của góc lượng giác \(\alpha \).

*Chú ý:

a, Trục tung là trục sin, trục hoành là trục côsin.

b, Với \(\alpha  \in \mathbb{R}\),\( - 1 \le {\mathop{\rm s}\nolimits} {\rm{inx}} \le 1, - 1 \le c{\rm{osx}} \le 1\).

\(\sin \alpha \)và \(\cos \alpha \) xác lập với từng \(\alpha  \in \mathbb{R}\).

\(\tan \alpha \) xác lập với những góc  \(\alpha  \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).

\(\cot \alpha \) xác lập với những góc  \(\alpha  \ne k\pi ,k \in \mathbb{Z}\).

c, Với từng góc lượng giác \(\alpha \) và số nguyên vẹn k, tao có:

\(\begin{array}{l}\sin \left( {\alpha  + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha  + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha  + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha  + k\pi } \right) = \cot \alpha \end{array}\)

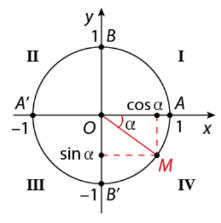
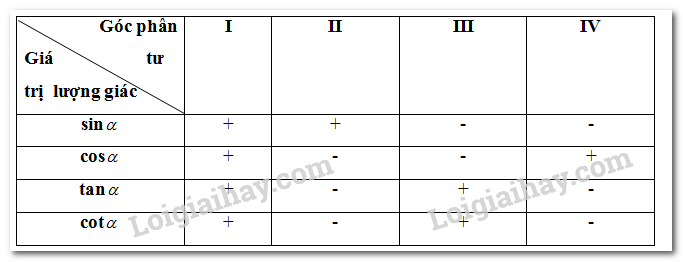
d, Bảng xác lập dấu của các giá trị lượng giác

 

Xem thêm: Danh Từ Trong Tiếng Anh (2024 mới) - EnglishCentral Blog

 

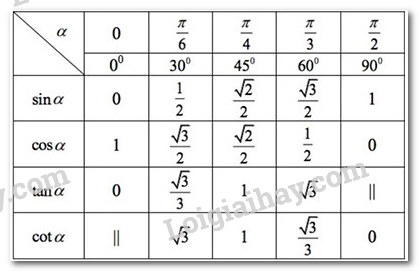
2. Giá trị lượng giác của một số trong những góc lượng giác quánh biệt

 

3. Sử dụng PC di động nhằm tính những độ quý hiếm lượng giác của một góc

- Lần lượt ấn những phím SHIFT \( \to \)MENU \( \to \)2 (CASIO 580VN)

Để lựa chọn đơn vị chức năng độ: ấn phím 1 (Degree).

Để lựa chọn đơn vị chức năng radian: ấn phím 2 (Radian).

- đè những phím MENU 1 nhằm nhập chính sách đo lường và tính toán.

II. Quan hệ trong những độ quý hiếm lượng giác

1. Các hệ thức cơ bạn dạng trong những độ quý hiếm lượng giác của một góc lượng giác

\(\begin{array}{l}{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha  \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha  \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha  = 1\left( {\alpha  \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)

2. Quan hệ trong những độ quý hiếm lượng giác của những góc lượng giác với tương quan quánh biệt

• Hai góc đối nhau \(\alpha \) và \( - \alpha \)

\(\begin{array}{l}\sin \left( { - \alpha } \right) =  - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) =  - \tan \alpha \\\cot \left( { - \alpha } \right) =  - \cot \alpha \end{array}\)

• Hai góc bù nhau (\(\alpha \) và \(\pi \)-\(\alpha \))

\(\begin{array}{l}\sin \left( {\pi  - \alpha } \right) = \sin \alpha \\\cos \left( {\pi  - \alpha } \right) =  - \cos \alpha \\\tan \left( {\pi  - \alpha } \right) =  - \tan \alpha \\\cot \left( {\pi  - \alpha } \right) =  - \cot \alpha \end{array}\)

Xem thêm: Thị Trấn trong Tiếng Anh là gì: Định Nghĩa, Ví Dụ Anh Việt

• Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}\)-\(\alpha \))

\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)

• Hai góc rộng lớn xoàng xĩnh \(\pi \)(\(\alpha \) và \(\pi \) + \(\alpha \))

\(\begin{array}{l}\sin \left( {\pi  + \alpha } \right) =  - \sin \alpha \\\cos \left( {\pi  + \alpha } \right) =  - \cos \alpha \\\tan \left( {\pi  + \alpha } \right) = \tan \alpha \\\cot \left( {\pi  + \alpha } \right) = \cot \alpha \end{array}\)