Định nghĩa và công thức tính diện tích đa giác
Cách tính diện tích đa giác đều, không đều dễ hiểu kèm ví dụ
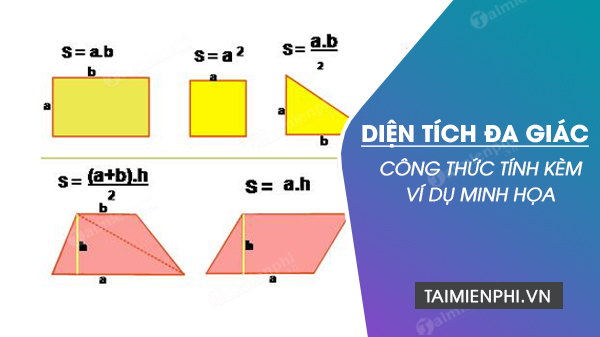
Mẹo học, tính toán nhanh diện tích đa giác theo quy ước chung
Mục Lục: Tìm hiểu về đa giác và cách tính diện tích
I. Định nghĩa, phân loại đa giác
1. Đa giác là gì?
Đa giác là hình khép kín bằng nhiều đoạn thẳng nối tiếp trên một mặt phẳng.
- Khu vực bị giới hạn bởi các đoạn thẳng gấp khúc tạo nên hình đa giác được gọi là phần trong của đa giác.
- Các đoạn thẳng trên đường gấp khúc của đa giác được xem là các cạnh của hình.
- Điểm kết nối giữa hai cạnh của đa giác được biết đến là đỉnh của hình đa giác.
- Đoạn thẳng nối hai đỉnh không kề nhau của đa giác được gọi là đường chéo của hình.
2. Phân loại đa giác
Đa giác có thể bao gồm đoạn thẳng (cạnh của đa giác) và các góc vô cùng lớn. Dưới đây là phân loại chi tiết:
- Đa giác lồi: Toàn bộ đa giác nằm về một phía của đường thẳng chứa cạnh bất kỳ của đa giác.
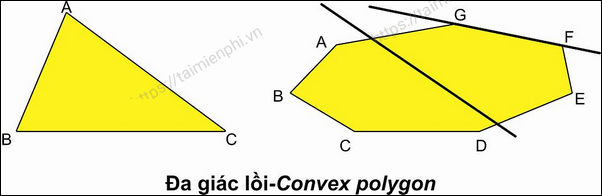
- Đa giác lõm: Đa giác nằm về 2 phía của ít nhất một đường thẳng chứa một cạnh của đa giác.
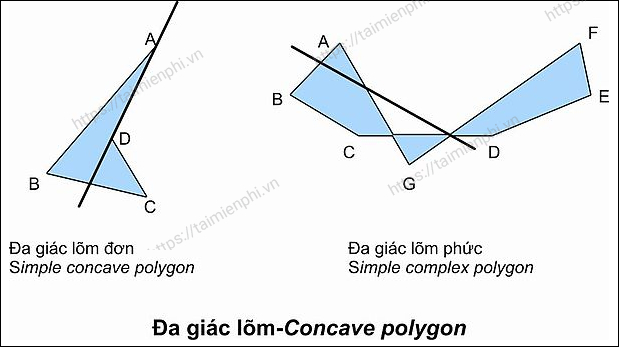
- Đa giác đơn: Các cạnh chỉ cắt nhau tại đỉnh của đa giác, không có hai cạnh không kề nhau cắt nhau.
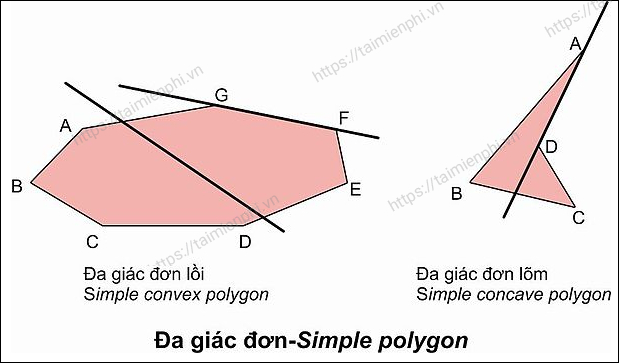
- Đa giác không đơn: Đa giác có hai cạnh không kề nhau cắt nhau (điểm cắt nhau không phải là đỉnh của đa giác).
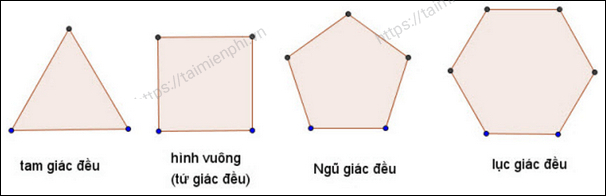
- Đa giác đều: Tất cả cạnh và góc trong đa giác đều bằng nhau. Đa giác đều thường xuất hiện trong toán học: Tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều...
II. Công thức tính diện tích đa giác bất kỳ kèm ví dụ
1. Công thức tính diện tích đa giác đều
1. Công thức tính diện tích đa giác đều
S = (a x p)/2
Trong đó:
- p là chu vi của đa giác (chu vi là tổng độ dài các cạnh của đa giác đó).
- a là chiều dài đoạn trung đoạn (trung đoạn là đoạn thẳng vuông góc với cạnh và đi qua tâm của đa giác).
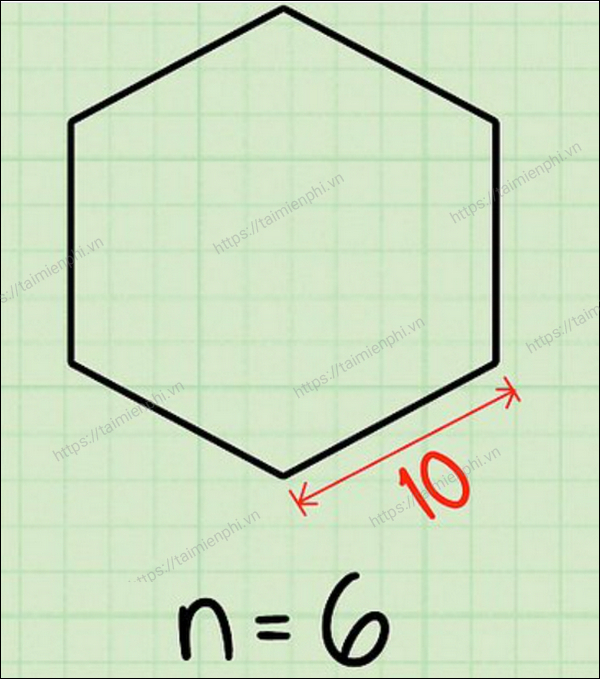
Ví dụ cách tính diện tích hình đa giác đều: Một lục giác đều có 6 cạnh (n) với mỗi cạnh (s) có độ dài là 10cm. Diện tích của đa giác đều này là bao nhiêu?
Giải:
Bước 1: Tính chu vi của hình lục giác.
p = 6 x 10 = 60cm.
Bước 2: Tính đoạn trung đoạn
Lục giác đều có 6 cạnh (n), mỗi cạnh độ dài là 10 (s). Áp dụng giá trị 6 và 10 cho n và s.
Áp dụng biểu thức:
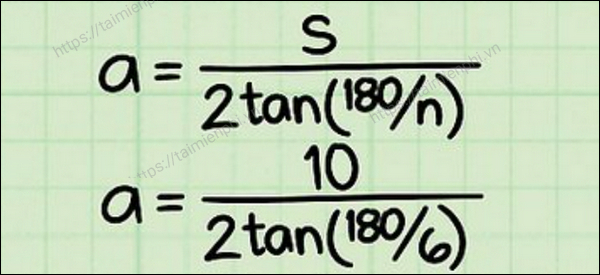
=> Kết quả của biểu thức 2tan(180/6) là 1,1547.
Tiếp tục, chia 10 cho 1,1547, thu được giá trị trung đoạn a là 8,66.
Bước 3: Tính diện tích đa giác đều
Diện tích = (a x p)/2 = (8,66 x 60)/2 = 259,8 (cm2).
2. Phương pháp tính diện tích đa giác không đều
2. Phương pháp tính diện tích đa giác không đều
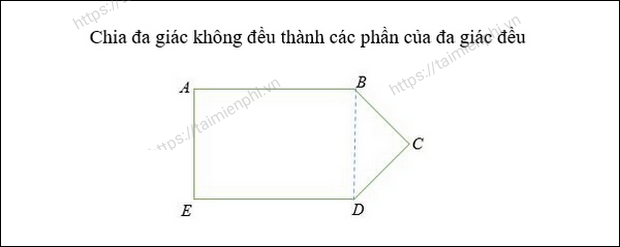
Bước 1: Chia đa giác thành các hình nhỏ như tam giác, vuông, thoi, bình hành...
Bước 2: Tính diện tích của từng hình đa giác nhỏ.
Bước 3: Tổng hợp diện tích của các đa giác nhỏ để tính diện tích của đa giác lớn.
(*) Phương pháp tính diện tích đa giác theo cách thông thường:
- Tính diện tích tam giác: S = 1/2 x chiều cao x độ dài cạnh đối diện của đỉnh.
- Tính diện tích hình vuông: S = Cạnh x cạnh.
- Tính diện tích hình bình hành: S = Chiều cao x đáy tương ứng.
- Tính diện tích hình chữ nhật: S = Chiều dài x chiều rộng.
Bài toán ví dụ: Cho một đa giác không đều có các cạnh là: AB = ED = 20 cm, BC = CD = 5 cm và AB = BD = 8 cm. Hãy tính diện tích đa giác đó.
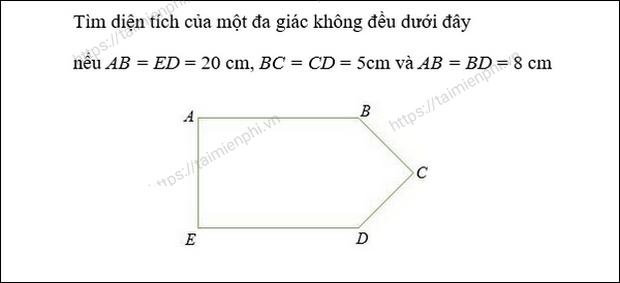
Giải:

III. Cách nhớ công thức tính diện tích đa giác bằng thơ
- Công thức tính diện tích hình thang: Muốn tính diện tích hình thang, đáy lớn và đáy nhỏ cộng lại, nhân với đường cao và chia đôi kết quả.
Cách tính diện tích hình thang
Đáy lớn, đáy nhỏ ta mang cộng vào
Rồi đem nhân với đường cao
Chia đôi kết quả thế nào cũng ra
- Công thức tính diện tích hình chữ nhật: Chữ nhật, dài nhân với rộng là xong ngay.
Chữ nhật em đã học qua
Dài nhân với rộng thế là ra ngay
- Công thức tính diện tích hình vuông: Hình vuông thật là tuyệt vời, cạnh nhân với cạnh ngay tức thì.
Hình vuông quả thật là hay
Cạnh nhân với cạnh ra ngay tức thì
- Công thức tính diện tích tam giác: Tam giác thì có khó chút, chiều cao nhân với độ dài đáy rồi chia đôi.
Tam giác thì có khó chi
Cao nhân với đáy ta thì chia đôi
- Công thức tính diện tích hình tròn: Hình tròn tính cũng dễ thôi, bán kính nhân pi là thành.
Hình tròn tính cũng dễ thôi
Bán kính, bán kính nhân pi là thành
- Cách tính diện tích hình bình hành: Bình hành diện tích không sai, chiều cao nhân đáy ai ai cũng làm.
Bình hành diện tích không sai
Chiều cao nhân đáy ai ai cũng làm.
Với thơ toán học, học sinh học cách tính diện tích đa giác đều, không đều,
Để tính diện tích hình chữ nhật, vuông, tam giác, và nhiều hình khác một cách dễ dàng.
Không chỉ tính diện tích, học thuộc cả công thức tính chu vi đa giác,
Quan trọng và cần thiết, kiến thức cơ bản đừng để lạc lõng.
Cùng học cách tính diện tích hình thang, thang cân, thang vuông sẽ được chia sẻ trong bài viết kế tiếp.
Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 2083 hoặc email: [email protected]