Từ vựng tiếng Anh về các cây gia vị
Trong tiếng Anh, 'turmeric' là củ nghệ, 'fennel' có nghĩa thì là.
Hình chóp là khối nhiều diện sở hữu lòng là 1 trong những nhiều giác và những mặt mày mặt là những tam giác sở hữu đỉnh chung.
Vì hình chóp không tồn tại nhiều đặc điểm “đẹp” giống như không tồn tại nhiều phần mềm nhập Toán học tập và thực dắt nên nhập phạm vi ngắn ngủi gọn gàng của nội dung bài viết này tôi chỉ trình diễn với chúng ta hình chóp đều và hình chóp cụt đều thôi ha.
Bạn đang xem: Tính diện tích và thể tích của hình chóp đều, hình chóp cụt đều
Cụ thể thì bản thân tiếp tục trình diễn khái niệm, công thức tính diện tích S, thể tích của hình chóp đều, hình chóp cụt đều và ví dụ minh họa.
#1. Định nghĩa hình về chóp đều và hình chóp cụt đều
Hình chóp đều là hình chóp sở hữu lòng là 1 trong những nhiều giác đều, những mặt mày mặt là những tam giác cân đối nhau, sở hữu đỉnh chung.
Người tớ thông thường gọi thương hiệu của hình chóp tất nhiên thương hiệu của nhiều giác lòng hình chóp <n> giác đều.
Với <n> có thể là tam giác, tứ giác, ngũ giác…..
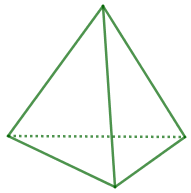
Hình chóp tam giác đều phải sở hữu lòng là 1 trong những hình tam giác đều, phụ vương mặt mày mặt là phụ vương tam giác cân đối nhau.
Nếu rời hình chóp đều bởi vì một phía phẳng phiu tuy nhiên song với mặt mày phẳng phiu lòng (đa giác đều) thì phần nằm trong lòng mặt mày phẳng phiu rời và mặt mày phẳng phiu lòng được gọi là hình chóp cụt đều.
Các chúng ta nhằm ý hình bên dưới, những mặt mày mặt của hình chóp cụt đều là những hình thang cân đối nhau.
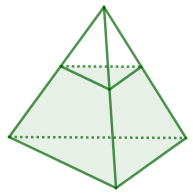
Hình chóp tam giác cụt đều phải sở hữu lòng là 1 trong những tam giác đều, phụ vương mặt mày mặt là phụ vương hình thanh cân đối nhau.
#2. Công thức tính diện tích S hình chóp đều và hình chóp cụt đều
2.1. Công thức tính diện tích S của hình chóp đều
Diện tích xung xung quanh của hình chóp đều sẽ bởi vì tích của nửa chu vi lòng và chừng lâu năm trung đoạn (đường cao kẻ kể từ đỉnh của một phía mặt mày bất kỳ)
Diện tích toàn phần của hình chóp đều tiếp tục bởi vì tổng của diện tích xung xung quanh và diện tích nhiều giác lòng.
2.2. Công thức tính diện tích S của hình chóp cụt đều
Diện tích xung xung quanh của hình chóp cụt đều sẽ được xem theo dõi công thức $S_{xq}=\frac{1}{2}.(C+C’).m$
Cchu vi nhiều giác lòng lớnC’chu vi nhiều giác lòng bémtrung đoạn của hình thang cân
Diện tích toàn phần của hình chóp cụt đều tiếp tục bởi vì tổng của diện tích xung xung quanh, diện tích S nhiều giác lòng rộng lớn và diện tích S nhiều giác lòng nhỏ xíu.
#3. Công thức tính thể tích hình chóp đều và hình chóp cụt đều
3.1. Công thức tính thể tích của hình chóp đều
Thể tích của hình chóp đều sẽ bởi vì tích của một phần phụ vương, diện tích S của nhiều giác lòng và chiều cao
3.2. Công thức tính thể tích của hình chóp cụt đều
Thể tích của hình chóp cụt đều sẽ được xem theo dõi công thức $V=\frac{1}{3}.(S+S’+\sqrt{S.S’}).h$
Sdiện tích S nhiều giác lòng lớnS’diện tích S nhiều giác lòng béhđộ cao của hình chóp cụt đều
#4. Ví dụ minh họa
Ví dụ 1: Tính diện tích S xung xung quanh, diện tích S toàn phần và thể tích của hình chóp tứ giác đều S.ABCD biết chừng lâu năm cạnh AB=30 centimet và chừng lâu năm cạnh SA=25 cm
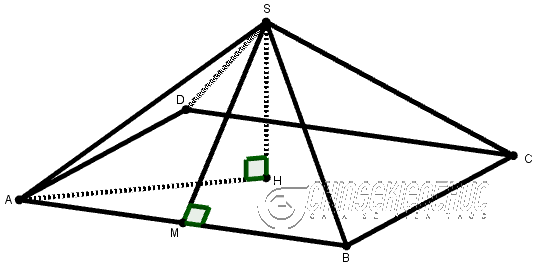
Lời Giải:
Diện tích xung xung quanh, diện tích S toàn phần
Qua S kẻ đường thẳng liền mạch vuông góc với AB bên trên M
Trước không còn tớ sở hữu đánh giá SM là đàng cao của tam giác cân nặng SAB (cân bên trên S) nên SM cũng chính là đàng trung tuyến
Suy rời khỏi $AM=\frac{1}{2}.AB=\frac{1}{2}.30=15~cm$
Vì tam giác SAM là tam giác vuông (vuông bên trên M) nên $SM=\sqrt{SA^2-MA^2}=\sqrt{25^2-15^2}=20~cm$
Diện tích xung xung quanh của hình chóp tứ giác đều S.ABCD tiếp tục bởi vì $\frac{4.30}{2}.20=60.20=1200~cm^2$
Diện tích toàn phần của hình chóp tứ giác đều S.ABCD tiếp tục bởi vì $1200+30^2=1200+900=2100~cm^2$
Thể tích của hình chóp
Qua S kẻ đường thẳng liền mạch vuông góc với tứ giác đều ABCD bên trên H
Vì tam giác SAH là tam giác vuông (vuông ở H) nên $SH=\sqrt{SA^2-HA^2}=\sqrt{25^2-(15\sqrt{2})^2}=5\sqrt{7} \approx 13.2~cm$
Thể tích của hình chóp tứ giác đều S.ABCD tiếp tục bởi vì $\frac{1}{3}.30^2.5\sqrt{7}=1500\sqrt{7} \approx 3968.6~cm^3$
Vậy diện tích S xung xung quanh, diện tích S toàn phần và thể tích của hình chóp vẫn mang đến thứu tự ngay sát bởi vì $1200~cm^2, 2100~cm^2, 3968.6~cm^3$
Chú ý: Cho một hình vuông vắn có tính lâu năm một cạnh bởi vì a, khi bấy giờ chừng lâu năm đàng chéo cánh tiếp tục bởi vì $a\sqrt{2}$
Ví dụ 2: Tính diện tích S xung xung quanh, diện tích S toàn phần và thể tích của hình chóp tam giác đều S.ABC biết chừng lâu năm cạnh AB và chừng lâu năm cạnh SA đều bởi vì a cm
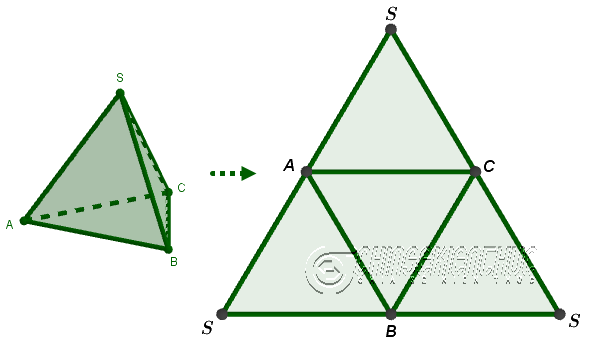
Trước Khi lần tòi điều giải của ví dụ này bản thân nài nhắc nhở lại một vài ba kiến thức và kỹ năng vẫn biết trước cơ.
Các kiến thức và kỹ năng này đã và đang được quá nhận, chúng ta chỉ việc vận dụng nhưng mà ko cần thiết minh chứng lại.
- Trong một tam giác đều đàng cao, đàng trung tuyến, đàng trung trực và đàng phân giác trùng nhau
- Nếu tam đều phải sở hữu chừng lâu năm một cạnh bởi vì a thì độ cao và diện tích S thứu tự bởi vì $\frac{a\sqrt{3}}{2}, \frac{a^2\sqrt{3}}{4}$
Lời Giải:
Dễ thấy chừng lâu năm trung đoạn của hình chóp đều bởi vì $\frac{a\sqrt{3}}{2}$
Suy rời khỏi diện tích S xung xung quanh của hình chóp đều tiếp tục bởi vì $\frac{3a}{2}.\frac{a\sqrt{3}}{2}=\frac{3a^2\sqrt{3}}{4}$
Dễ thấy diện tích S của tam giác đều bởi vì $\frac{a^2\sqrt{3}}{4}$
Suy rời khỏi diện tích S toàn phần của hình chóp đều tiếp tục bởi vì $\frac{3a^2\sqrt{3}}{4}+\frac{a^2\sqrt{3}}{4}=a^2\sqrt{3}$
Chiều cao của hình chóp đều bởi vì $\sqrt{a^2-\left(\frac{2}{3}\frac{a\sqrt{3}}{2}\right)^2}=\cdots=\frac{a\sqrt{6}}{3}$
Suy rời khỏi thể tích của hình chóp đều tiếp tục bởi vì $\frac{1}{3}.\frac{a^2\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}$
=$\frac{a^3\sqrt{2}}{12}$
Vậy diện tích S xung xung quanh, diện tích S toàn phần và thể tích của hình chóp tam giác đều S.ABC thứu tự bởi vì $\frac{3a^2\sqrt{3}}{4}, a^2\sqrt{3}, \frac{a^3\sqrt{2}}{12}$
#5. Lời kết
Như vậy tất cả chúng ta vẫn bên nhau lần hiểu đoạn về phương pháp tính diện tích S xung xung quanh, diện tích S toàn phần, giống như phương pháp tính thể tích của hình chóp đều và hình chóp cụt đều rồi nhé.
Trong nội dung bài viết này tôi chỉ trình diễn ví dụ cho chính mình về hình chóp đều, hình chóp cụt đều thì ko trình diễn. Nếu ham muốn chúng ta cũng có thể tự động lần hiểu tăng, phương pháp tính trọn vẹn tương tự động chỉ việc vận dụng đích công thức là đoạn.
Hi vọng nội dung bài viết này tiếp tục hữu ích với chúng ta. Xin Chào thân ái và hứa hội ngộ chúng ta trong mỗi nội dung bài viết tiếp sau nhé !
Đọc thêm:
Xem thêm: 100+ Từ vựng các loại trái cây bằng tiếng Anh cho bé
- Cách tính diện tích S và thể tích của hình trụ (có ví dụ)
- Tính diện tích S, thể tích của hình lăng trụ đứng tam giác, tứ giác
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài ghi chép đạt: 5/5 sao - (Có 1 lượt tiến công giá)
Note: Bài ghi chép này hữu ích với chúng ta chứ? Đừng quên review nội dung bài viết, lượt thích và share mang đến bè bạn và người thân trong gia đình của khách hàng nhé !