Ngoài các bài tập đại số, các bạn học sinh lớp 5 cũng sẽ tiếp cận với các bài tập liên quan đến hình học. Trong bài viết này, Hoàng Hà Mobile sẽ tổng hợp công thức tính đường cao tam giác cân, đều, vuông, thường. Bạn cũng có thể xem một số dạng bài tập và lưu ý để có thể ôn tập hiệu quả nhé!
Hình học là một trong những phần kiến thức quan trọng trong phân phối chương trình của các bạn học sinh. Các dạng toán với hình học không chỉ đa dạng mà cũng có rất nhiều công thức cần ghi nhớ để áp dụng. Các bạn học sinh đã được làm quen với các hình học từ rất sớm. Hình tam giác cũng không quá khó để nhận biết.
Trong toán học, khái niệm về hình tam giác là một hình có ba cạnh ba đỉnh, 3 cạnh là 3 đoạn thẳng nối các đỉnh đó. Trong đó, 3 đỉnh cũng không thẳng hàng với nhau. Chính vì tính chất này, hình tam giác có ba góc, và các góc có độ lớn khác nhau. Các cạnh của hình tam giác cũng có độ dài khác nhau.
Một số hình tam giác đặc biệt sẽ có các cạnh bằng nhau, hoặc các góc độ đặc biệt, như góc vuông 90 độ chẳng hạng. Vì thế đã tạo nên một số trường hợp tam giác đặc biệt. Vậy đường cao là gì và đường cao tam giác cân, đều, vuông có khác gì so với tam giác thông thường?
Đường cao trong hình tam giác là gì?
Trong tam giác, ngoài các cạnh, các góc, còn một yếu tố nữa cần quan tâm đó là đường cao. Đường cao trong tam giác bất kỳ được hiểu là một đoạn kẻ vuông góc từ đỉnh đến đường thẳng chứa cạnh đối diện. Ví dụ như trong hình bên dưới bạn có thể thấy, AH được coi là đường cao của tam giác ABC. Đường cao AH xuất phát từ đỉnh A của tam giác ABC.
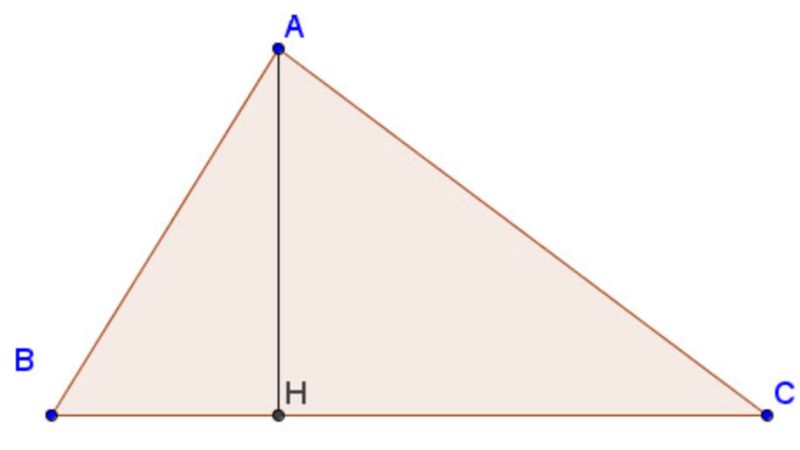
Trong một tam giác, vì có ba cạnh nên cũng sẽ có ba đường cao tương ứng với các cạnh đó. Đường cao trong từng loại tam giác đặc biệt như cân, đều hoặc vuông sẽ có thêm một số tính chất đặc biệt. Tuy nhiên cơ bản nó vẫn đảm bảo được tính chất là vuông góc với cạnh đối diện và được kẻ từ một đỉnh của tam giác.
Công thức tính đường cao tam giác cân, đều, vuông, thường
Nếu bạn chưa biết thì hầu hết các hình học phẳng cơ bản đều có rất nhiều công thức để tính các cạnh, tính chu vi, tính diện tích. Và trong tam giác cũng có rất nhiều công thức để tính đường cao. Tuy nhiên, tuỳ theo từng loại tam giác đặc biệt thì đường cao của nó sẽ có những cách tính khác nhau.
Trường hợp 1: Tính đường cao tam giác thường
Đối với trường hợp tam giác thông thường, là loại tam giác có ba cạnh, ba đỉnh như đã giới thiệu ở trên. Chúng ta sẽ áp dụng công thức Heron để tính được đường cao cho tam giác. Như trong hình, bạn sẽ thấy hình tam giác ABC có đường cao h. Để có thể tính được độ dài đường cao h, chúng ta sẽ áp dụng công thức:
Trong đó:
a, b, c lần lượt là độ dài các cạnh của hình tam giác. Thông thường, đề bài sẽ cho sẵn dữ kiện này
ha là đường cao h được kẻ từ đỉnh A của hình tam giác xuống cạnh BC.
p là nửa chu vi của hình tam giác ABC. Nửa chu vi của hình tam giác sẽ tính theo công thức là:
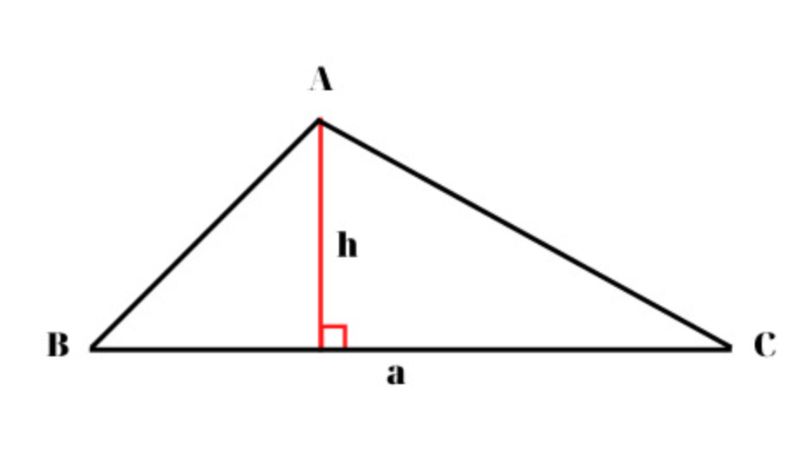
Đối với các bài toán tính đường cao cho độ dài các cạnh, bạn sẽ cần làm lần lượt từ bước tính nửa chu vi p trước. Sau đó chỉ cần áp dụng công thức Heron trên là có thể tính được độ dài đường cao rồi.
Một số bài tập ví dụ:
Bài 1: Cho tam giác ABC, trong đó cạnh AB = 3 cm, cạnh BC = 7 cm, cạnh AC = 6 cm. Hãy tính đường cao AH kẻ từ A cắt BC tại H và diện tích của hình tam giác ABC.
Bài 2: Cho tam giác ABC, trong đó cạnh AB = 5 cm, cạnh BC = 9 cm, cạnh AC = 4 cm. Hãy tính đường cao BH kẻ từ B cắt AC tại H và diện tích của hình tam giác ABC
Trường hợp 2: Tính đường cao tam giác cân
Với trường hợp tam giác trong đề bài cho sẵn là tam giác cân. Bạn cần phải hiểu qua về tính chất của loại tam giác đặc biệt này. Tam giác cân là một hình tam giác mà trong đó có hai cạnh bằng nhau. Như vậy, đỉnh của tam giác cân sẽ là điểm nằm giữa hai cạnh bằng nhau. Bạn có thể xem hình minh hoạ ở dưới để có thể hiểu hơn. Khi kẻ một đường cao từ đỉnh cân của giác, thì nó sẽ được tính theo công thức như sau:
Ví dụ như trong hình, tam giác ABC có hai cạnh AC và AB bằng nhau, vì thế nó cân tại đỉnh A. Trong đó, AH là đường cao, thì AH sẽ đồng thời là đường trung tuyến, H là trung điểm của đoạn thẳng BC. Như vậy:
⇒ HB=HC= ½BC
Lúc này, chúng ta sẽ áp dụng định lý Pytago cho tam giác vuông ABH vuông tại H (hoặc tam giác ACH) ta có:
AH²+BH²=AB²
⇒AH²=AB²−BH²
Vì tính chất đặc biệt của hình này nên đường cao tam giác cân sẽ được áp dụng theo định lý Pytago để tính được như cách trên.

Một số bài tập ví dụ:
Bài 1: Cho tam giác ABC cân tại A, có đường cao AH, biết AB = AC = 5; BC = 4 cm. Hãy tính độ dài đường cao AH và diện tích của tam giác ABC.
Trường hợp 3: Tính đường cao tam giác vuông
Một loại thứ hình đặc biệt thứ ba bạn cần biết đó là tam giác vuông. Theo khái niệm, tam giác vuông là tam giác có một góc trong đó là góc vuông (hay góc 90 độ). Nó sẽ có một số tính chất đặc biệt và các công thức liên quan để có thể tính được các cạnh, các góc trong hình khác. Bạn có thể xem trong hình bên dưới đây.
Giả sử nếu như ABC là một tam giác vuông tại A. Trong đó h là đường cao được kẻ từ điểm A xuống cạnh đối diện BC. Vậy thì, ta sẽ có cách để các cạnh và đường cao trong tam giác vuông như sau:
1. a2 = b2 + c2
2. b2 = a.b′ và c2 = a.c′
3. a.h = b.c
4. h2 = b′.c’
5.
Trong đó ta có:
a, b, c là độ dài các cạnh của tam giác vuông ABC trên hình.
b’ được gọi là đường chiếu của cạnh b
c’ được gọi là đường chiếu của cạnh c
h chính là đường cao của tam giác vuông kẻ từ đỉnh A xuống cạnh huyền BC.
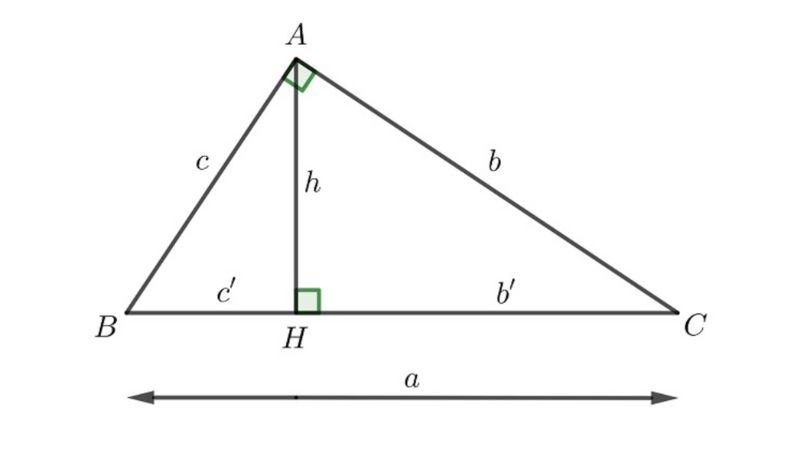
Vì tam giác ABC vuông ở đỉnh A có những tính chất khác biệt so với đường cao tam giác cân vì thế bạn cũng cần ghi nhớ công thức trên để có thể giải các bài toán liên quan đến loại tam giác này.
Một số bài tập ví dụ:
Bài 1: Cho tam giác ABC vuông tại A, có đường cao AH, biết AB : AC = 3; AB + AC = 21cm. Hãy tính độ dài các cạnh của tam giác ABC và tính đường cao AH.
Trường hợp 4: Tính đường cao tam giác đều
Cuối cùng, một loại tam giác đặc biệt khác đó là tam giác đều. Trong hình học phẳng, tam giác đều đươc định nghĩa là loại tam giác có ba cạnh bằng nhau. Tương đương với đó chúng ta cũng sẽ có ba góc bằng nhau. Vì tổng các góc trong một tam giác bằng 180 độ do đó hình tam giác đều sẽ có ba góc 60 độ. Đây là loại tam giác còn đặc biệt hơn cả tam giác cân. Vì thế, cách tính đường cao của nó cũng có những khác biệt trong công thức.
Giả sử như tam giác ABC trong hình là một tam giác đều. Như vậy, cạnh AB, AC hay BC đều có một độ dài chung là a. Khi đó, ta kẻ một đường vuông góc từ đỉnh A xuống cạnh BC. Lúc này, h là đường cao của tam giác đều ABC. Thay vì tính như đường cao tam giác cân, bạn sẽ cần áp dụng công thức như sau:
Trong đó ta có:
h là đường cao của tam giác đều.
a là độ dài cạnh của tam giác đều.
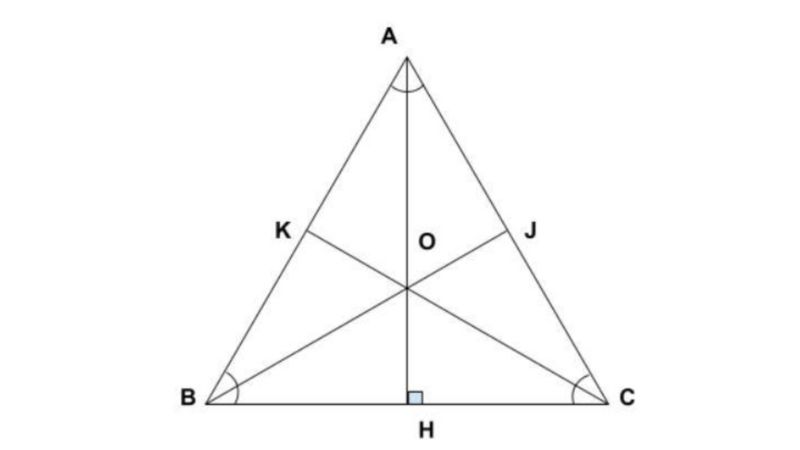
Tóm lại, mỗi loại hình tam giác sẽ có công thức tính khác nhau. Bạn cần phải nắm vững các công thức và tính chất riêng của từng loại mới có thể giải được các bài toán liên quan đến tính đường cao trong tam giác.
Một số bài tập ví dụ:
Bài 1: Cho tam giác ABC là tam giác đều với đường cao AH, biết mỗi cạnh của hình tam giác này có độ dài bằng 6. Hãy tính độ dài đường cao AH và diện tích của hình tam giác ABC.
Một số tính chất khác của đường cao trong tam giác
Ngoài những công thức trên để bạn có thể tính được đường cao tam giác cân, đều, vuông và thường, các đường cao trong tam giác cũng có rất nhiều tính chất khác bạn nên biết để áp dụng khi cần.
- Ba đường cao trong một tam giác sẽ cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
- Trong tam giác cân, đường cao tương ứng với đáy kẻ từ đỉnh của hai cạnh bằng nhau sẽ đồng thời là đường phân giác, đường trung tuyến, đường trung trực.
- Trong tam giác đều, các điểm: trọng tâm, trực tâm sẽ nằm trong tam giác và cách đều 3 đỉnh, 3 cạnh.
Những lưu ý khi làm dạng toán tính đường cao tam giác cân, vuông, đều, thường
Dạng toán tính độ dài đường cao trong tam giác cơ bản không phải một dạng toán khó. Tuy nhiên, nếu bạn không nắm vững các lưu ý sau thì vẫn có thể bị mất điểm khi làm bài.
Đầu tiên, bạn phải xác định đúng loại tam giác mà đề cho. Đó là tam giác thường, vuông, cân hay đều và đi kèm với đó là những dữ kiện gì. Việc xác định đúng loại tam giác sẽ giúp bạn xác định được cách làm đúng.
Sau đó, hãy ôn tập và nhớ kỹ các công thức. Dựa trên những dữ kiện mà đề bài cho để áp dụng vào từng công thức sao cho phù hợp.
Một lưu ý nữa khi làm bài tập về hình tam giác đó là các đại lượng phải cùng một đơn vị đo. Thông thường các bài toán sẽ có những dữ kiện khác đơn vị đo để tăng mức độ khó cho từng bài. Vì thế bạn hãy lưu ý đơn vị để tránh lỗi sai này nhé. Cuối cùng là kiểm tra kỹ lại bài trước khi nộp để đạt được điểm số cao nhất.
Tạm kết
Hoàng Hà Mobile đã giới thiệu cho bạn công thức tính đường cao tam giác cân, vuông, đều và thường. Bạn có thể xem một số bài tập áp dụng và lưu ý để làm bài đạt kết quả tốt nhất nhé
Trên đây là bài viết thông tin về công thức tính đường cao tam giác cân, vuông, đều và thường. Nội dung này có hữu ích với bạn không? Hãy để lại comment bên dưới nhé. Hoàng Hà Mobile sẽ tiếp tục cập nhật thông tin trong thời gian tới. Hãy theo dõi trang tin tức Hoàng Hà Mobile để cập nhật những thông tin công nghệ mới nhất nhé. Và đừng quên truy cập kênh YouTube Hoàng Hà Channel để cập nhật nhiều hơn những tin tức công nghệ nóng hổi.
Xem thêm:
- Số thực là gì? Một số dạng toán học phổ biến về số thực
- Cách giải phương trình bậc 2 nhanh chóng nhất










