1. Định nghĩa Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).
1. Định nghĩa
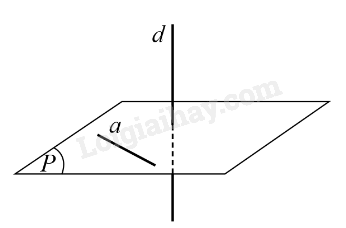
Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Nhận xét: Ta có thể chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc với một mặt phẳng chứa đường thẳng kia.
3. Tính chất
- Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
- Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
- Tính chất 3:
Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Tính chất 4:
Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
5. Phép chiếu vuông góc
Cho mặt phẳng (P) và một điểm M tuỳ ý trong không gian. Lấy đường thẳng d đi qua M và vuông góc với (P), gọi giao điểm của d và (P) là M’. Điểm M’ gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M trên (P).
Cho mặt phẳng (P). Quy tắc đặt tương ứng mỗi điểm M trong không gian với hình chiếu vuông góc M’ của điểm đó lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).
Nhận xét: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.
6. Định lí ba đường vuông góc
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng d nằm trong mặt phẳng (P). Khi đó, d vuông góc với a khi và chỉ khi d vuông góc với hình chiếu a’ của a trên (P).
Bình luận
![]() Chia sẻ
Chia sẻ
-
Giải hoạt động mở đầu trang 80 SGK Toán 11 tập 2 – Cánh Diều
Trong Hình 9, cột gỗ thẳng đứng và sàn nhà nằm ngang gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng.
-
Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cánh Diều
Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà.
-
Giải mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d
-
Giải mục 3 trang 81, 82 SGK Toán 11 tập 2 - Cánh Diều
Cho điểm O và đường thẳng a.
-
Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P).
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.