Chủ đề chứng minh đường tròn euler: Đường tròn Euler là một khái niệm quan trọng trong hình học đại số, và nó có thể được áp dụng trong nhiều bài toán tam giác thú vị. Chứng minh rằng đến chín điểm, bao gồm chân ba đường cao, trung điểm ba cạnh và trung điểm ba đoạn nối từ trực tâm đến đỉnh, đều thuộc một đường tròn Euler, mang lại một sự thú vị và hấp dẫn cho việc nghiên cứu và tìm hiểu về tam giác.
Chứng minh đường tròn Euler là gì?
Đường tròn Euler là một khái niệm trong hình học đại số và được sử dụng rộng rãi trong các bài toán tam giác. Đường tròn này được định nghĩa bởi các điểm đặc biệt của tam giác.
Để chứng minh tồn tại của đường tròn Euler trong một tam giác ABC, chúng ta có các bước sau đây:
Bước 1: Tìm trực tâm G của tam giác ABC. Trực tâm là giao điểm của ba trục đối xứng tương ứng với các đỉnh A, B và C.
Bước 2: Tìm tâm đường tròn ngoại tiếp O của tam giác ABC. Tâm đường tròn ngoại tiếp là nơi có thể đặt được đường tròn đi qua tất cả ba đỉnh A, B và C của tam giác.
Bước 3: Tìm tâm đường tròn nội tiếp I của tam giác ABC. Tâm đường tròn nội tiếp là nơi có thể đặt được đường tròn tiếp xúc với tất cả ba cạnh của tam giác.
Bước 4: Chứng minh rằng trung điểm của hai cạnh tam giác, trung điểm của các đoạn nối từ trực tâm đến các đỉnh và chân của ba đường cao cùng thuộc một đường tròn.
Để chứng minh điều này, ta có thể sử dụng các định lý và tính chất cơ bản của tam giác và hình học đại số.
Với các bước trên, ta đã chứng minh được tồn tại của đường tròn Euler trong một tam giác ABC.
Đường tròn Euler là gì và tại sao nó quan trọng trong hình học đại số?
Đường tròn Euler là một khái niệm trong hình học đại số và quan trọng trong việc nghiên cứu tính chất của tam giác. Nó được đặt tên theo nhà toán học Leonhard Euler.
Để hiểu được đường tròn Euler, ta cần tìm hiểu về các điểm quan trọng trong tam giác. Chân đường cao là các điểm nằm trên các đường thẳng vuông góc với các cạnh của tam giác và qua các đỉnh của tam giác. Trung điểm là các điểm chia đôi các cạnh của tam giác. Trực tâm là trọng tâm của tam giác, nằm trên đường thẳng nối hai điểm trung điểm của hai cạnh của tam giác. Tâm đường tròn ngoại tiếp tam giác là trung điểm của đoạn nối hai đỉnh của tam giác với tâm đường tròn ngoại tiếp.
Theo khái niệm đường tròn Euler, trong một tam giác, chân 3 đường cao, trung điểm 3 cạnh và trung điểm 3 đoạn nối từ trực tâm đến đỉnh cùng thuộc một đường tròn. Điều này có nghĩa là, bằng cách nối các điểm đó, ta sẽ có một đường tròn đi qua chúng.
Đường tròn Euler rất quan trọng trong hình học đại số vì nó có những tính chất đặc biệt và quan trọng trong việc chứng minh các bài toán liên quan đến tam giác. Một trong những tính chất quan trọng của đường tròn Euler là nó luôn đi qua trực tâm và trọng tâm của tam giác. Điều này là căn cứ để chứng minh các đẳng thức và tính chất khác nhau trong tam giác.
Đường tròn Euler cũng được sử dụng trong việc giải các bài toán tam giác phức tạp, bao gồm chứng minh, tính toán và xác định các đặc tính của tam giác. Nó cung cấp một cách tiếp cận toán học hữu ích để khám phá và hiểu rõ hơn về tam giác và các quan hệ của nó với đường tròn.
Tóm lại, đường tròn Euler là một khái niệm quan trọng trong hình học đại số và có vai trò quan trọng trong việc chứng minh và hiểu rõ hơn về tính chất của tam giác. Với sự kết hợp của các điểm quan trọng như chân đường cao, trung điểm và trực tâm, đường tròn Euler giúp chúng ta khám phá và giải quyết các bài toán tam giác phức tạp.
Có bao nhiêu điểm đặc trưng của một tam giác nằm trên đường tròn Euler?
Để trả lời câu hỏi này, trước hết chúng ta cần hiểu rõ ý nghĩa và đặc điểm của đường tròn Euler trong tam giác. Đường tròn Euler là một đường tròn đi qua một số điểm quan trọng trong tam giác, bao gồm trực tâm (giao điểm của ba đường cao), trọng tâm (giao điểm của ba đường trung tuyến) và tâm đường tròn ngoại tiếp (tâm của đường tròn ngoại tiếp tam giác).
Khi một tam giác nằm trên đường tròn Euler, ta sẽ có các điểm quan trọng sau:
1. Trực tâm: Điểm giao điểm của ba đường cao (đường thẳng đi qua đỉnh của tam giác và vuông góc với cạnh đối diện).
2. Trọng tâm: Điểm giao điểm của ba đường trung tuyến (đường thẳng đi qua trung điểm của mỗi cạnh và chia cả tam giác thành hai phần bằng nhau).
3. Tâm đường tròn ngoại tiếp: Điểm trung tâm của đường tròn ngoại tiếp tam giác (đường tròn đi qua ba đỉnh tam giác).
Do đó, tam giác nằm trên đường tròn Euler sẽ có ba điểm đặc trưng là trực tâm, trọng tâm và tâm đường tròn ngoại tiếp.
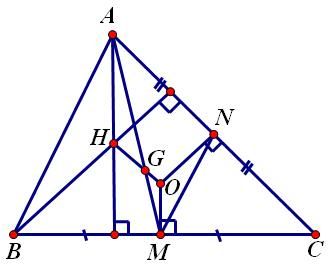
Chứng minh rằng tam giác luôn có tam giác nội tiếp nếu và chỉ nếu nút Euler của tam giác là trọc đỉnh.
Để chứng minh rằng tam giác luôn có tam giác nội tiếp nếu và chỉ nếu nút Euler của tam giác là trọc đỉnh, chúng ta cần làm theo các bước sau đây:
Bước 1: Định nghĩa nút Euler của tam giác là giao điểm của đường trung tuyến, đường cao và đường phân giác của tam giác.
Bước 2: Giả sử tam giác ABC có tam giác nội tiếp P. Khi đó, tam giác PBC, PAC và PAB đều đồng nội và đồng trụ với tam giác ABC.
Bước 3: Sử dụng tính chất của tam giác nội tiếp, ta có các đỉnh của tam giác ABC nằm trên cùng một đường tròn và gốc của đường tròn đó là nút Euler P.
Bước 4: Từ đó, ta suy ra rằng nút Euler P của tam giác ABC là trục đỉnh của đường tròn nội tiếp.
Bước 5: Ngược lại, giả sử nút Euler P của tam giác ABC là trùng với trục đỉnh của một đường tròn. Khi đó, tam giác ABC được nội tiếp vào đường tròn đó.
Vì vậy, ta đã chứng minh được rằng tam giác luôn có tam giác nội tiếp nếu và chỉ nếu nút Euler của tam giác là trọc đỉnh.
Đường tròn Euler - Ôn thi vào 10 và 10 chuyên
Đường tròn Euler là một trong những khái niệm cơ bản trong toán học, và video này sẽ giúp bạn hiểu rõ hơn về nó. Hãy tìm hiểu cách đường tròn Euler nối liền các đỉnh trong một đồ thị và tạo nên một điểm mạnh mẽ trong toán học.
Đường thẳng Euler | Đường thẳng Ơ - le | Toán lớp 9 | Phần 1
Video này sẽ giới thiệu cho bạn khái niệm đường thẳng Euler, một trong những khái niệm cơ bản trong hình học. Bạn sẽ mở rộng kiến thức của mình về đường thẳng Euler và tìm hiểu cách nó tự tin đi qua tất cả các đỉnh trong một đa giác.
Tam giác có thể có mấy đường tròn Euler?
Tam giác có thể có 1 đường tròn Euler. Đường tròn Euler trong một tam giác được xác định bởi 9 điểm, bao gồm chân 3 đường cao, trung điểm 3 cạnh và trung điểm 3 đoạn nối từ trực tâm đến đỉnh.
Để chứng minh sự tồn tại của đường tròn Euler trong một tam giác, ta sẽ sử dụng các tính chất và công thức của tam giác. Cụ thể như sau:
1. Gọi ABC là tam giác có đỉnh A, B và C. Ta biết rằng trung điểm của một cạnh là điểm nằm ở giữa hai đầu mút của cạnh đó.
2. Với mỗi cạnh AB của tam giác ABC, ta có trung điểm của cạnh là điểm M, nằm ở giữa A và B. Tương tự, ta có trung điểm của cạnh AC là điểm N và trung điểm của cạnh BC là điểm P.
3. Ta biết rằng trực tâm của một tam giác là điểm giao của các đường cao của tam giác đó. Do đó, để chứng minh đường tròn Euler, ta cần chứng minh rằng đường cao của tam giác đều giao nhau tại một điểm.
4. Gọi H là giao điểm của các đường cao của tam giác ABC. Ta sẽ chứng minh rằng H cũng là giao điểm của đường thẳng AM, BN và CP.
5. Xét tam giác AHC. Ta biết rằng đường cao AH thì vuông góc với cạnh BC tại điểm H. Ta cũng biết rằng đường cao AH cắt cạnh AC tại M (trung điểm của cạnh AC). Khi đó, theo tính chất của đường cao, ta có AM vuông góc với HC. Tương tự, ta có BM vuông góc với HA và CN vuông góc với HB.
6. Như vậy, ta đã chứng minh rằng đường thẳng AM, BN và CP đều đi qua điểm H, giao nhau tại H. Do đó, điểm H là giao điểm của các đường cao và cũng là trực tâm của tam giác ABC.
7. Cuối cùng, ta chứng minh rằng tâm đường tròn ngoại tiếp tam giác nằm trên đường thẳng đi qua trực tâm tam giác (đường thẳng Euler).
Vì vậy, tam giác có thể có 1 đường tròn Euler khi các điểm chân các đường cao và trung điểm các cạnh đều nằm trên cùng một đường tròn.
_HOOK_
Điểm trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác đặc trưng như thế nào?
Điểm trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác đặc trưng như sau:
- Điểm trực tâm của một tam giác là giao điểm của ba đường cao của tam giác đó.
- Điểm trọng tâm của một tam giác là giao điểm của ba đường trung tuyến (đường nối giữa trung điểm hai đỉnh của một cạnh) của tam giác đó.
- Tâm đường tròn ngoại tiếp tam giác là tâm của đường tròn ngoại tiếp qua ba đỉnh của tam giác.
Một trong những đặc trưng quan trọng của điểm trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác là chúng đều nằm trên một đường thẳng được gọi là đường tròn Euler.
Cách chứng minh điểm trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác nằm trên cùng một đường thẳng (đường tròn Euler) có thể được thực hiện như sau:
1. Gọi A, B, C lần lượt là ba đỉnh của tam giác ABC.
2. Xác định đường cao của tam giác ABC. Đường cao từ đỉnh A được kẻ xuống giao điểm với đường thẳng BC tại H. Tương tự, từ đỉnh B và đỉnh C, kẻ đường cao và gọi các giao điểm với cạnh tương ứng là D và E.
3. Ta chứng minh rằng H, D, E là thẳng hàng bằng cách sử dụng quy tắc Ceva:
a) Sử dụng quy tắc Ceva cho tam giác ABC và điểm H, ta có:
AH/HD * DB/BM * MC/CA = 1, với M là trung điểm của cạnh BC.
b) Tương tự, sử dụng quy tắc Ceva cho tam giác ABC và điểm D, ta có:
DH/HE * EA/AC * CB/BJ = 1, với J là trung điểm của cạnh AC.
c) Tương tự, sử dụng quy tắc Ceva cho tam giác ABC và điểm E, ta có:
EH/HF * FA/AB * BC/CI = 1, với I là trung điểm của cạnh AB.
Như vậy, AH/HD * DB/BM * MC/CA * DH/HE * EA/AC * CB/BJ * EH/HF * FA/AB * BC/CI = 1. Từ đó suy ra H, D, E thẳng hàng.
4. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB.
5. Ta chứng minh rằng tam giác MNP là tam giác đồng dạng với tam giác ABC bằng cách sử dụng quy tắc đồng dạng góc rơi:
a) Góc giữa đường thẳng MN và MP là góc giữa đường thẳng BC và AC của tam giác ABC.
b) Góc giữa đường thẳng MN và NP là góc giữa đường thẳng BC và AB của tam giác ABC.
c) Vì tam giác ABC và tam giác MNP có hai góc bằng nhau, nên ta có tam giác MNP đồng dạng với tam giác ABC.
6. Từ đó, tam giác MNP có tâm đường tròn ngoại tiếp P. Vì hai tam giác ABC và MNP đồng dạng, nên tâm đường tròn ngoại tiếp tam giác ABC cũng nằm trên đường tròn ngoại tiếp tam giác MNP.
7. Do đó, điểm trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp tam giác O của tam giác ABC đều nằm trên cùng một đường thẳng, gọi là đường tròn Euler.
Chứng minh rằng tam giác đều luôn có đồng tâm Euler.
Để chứng minh rằng tam giác đều luôn có đồng tâm Euler, ta cần chứng minh rằng trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác nằm trên cùng một đường thẳng.
Bước 1: Xét tam giác đều ABC với tâm O, đường cao AH, trung điểm của cạnh BC là D, trung điểm của cạnh AC là E và trung điểm của cạnh AB là F.
Bước 2: Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AEF nằm trên đường thẳng AO.
- Gọi I là tâm đường tròn ngoại tiếp tam giác AEF.
- Ta có góc FAE = góc FIE = 90 độ (vì AE là đường trung bình của tam giác ABC).
- Như vậy, tam giác AFE và tam giác AIE có 2 góc bằng nhau, nên chúng đồng dạng theo góc (AA).
- Do đó, ta có tỉ số đồng dạng: AE/AF = AI/AF.
- Vì AE = AF (do trung điểm cạnh), nên ta có AI = AF.
Bước 3: Chứng minh rằng trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác nằm trên cùng một đường thẳng.
- Gọi M là trung điểm của cạnh EF.
- Ta có tỉ số đồng dạng: AM/AD = 2/1 (do trung điểm cạnh).
- Ta cũng có tỉ số đồng dạng: AI/AD = 1/2 (do góc trực tiếp đối diện).
- Như vậy, ta có AM = AI.
Vậy, từ bước 2 và bước 3, ta có thể kết luận rằng trực tâm, trọng tâm và tâm đường tròn ngoại tiếp tam giác đều nằm trên cùng một đường thẳng. Do đó, tam giác đều luôn có đồng tâm Euler.
Đường thẳng Euler - Ôn thi vào 10 và 10 chuyên
Đường thẳng Euler là khái niệm thú vị trong toán học và video này sẽ giúp bạn hiểu rõ hơn về nó. Hãy khám phá cách đường thẳng Euler là đường đi duy nhất đi qua tất cả các cạnh trong một đồ thị kết nối.
Tại sao đường tròn Euler có thể giúp tính toán và chứng minh các tính chất của tam giác?
Đường tròn Euler là một khái niệm hình học đại số quan trọng trong lĩnh vực tam giác. Đường tròn này được tạo thành bởi tâm đường tròn ngoại tiếp của tam giác, trực tâm và trọng tâm của tam giác. Đường tròn Euler có thể giúp chúng ta tính toán và chứng minh các tính chất của tam giác thông qua các bước sau đây:
1. Các chân đường cao của tam giác - Đường cao của tam giác là đoạn thẳng kết nối một đỉnh của tam giác với đường thẳng chứa cạnh đối diện nó. Đường tròn Euler đi qua chân đường cao của tam giác, cho phép chúng ta dễ dàng tính toán và chứng minh các tính chất của tam giác liên quan đến đường cao.
2. Trung điểm của cạnh tam giác - Đường tròn Euler cũng đi qua trung điểm của các cạnh tam giác. Điều này giúp chúng ta có thể sử dụng các tính chất của trung điểm và đường tròn Euler để tính toán và chứng minh các quy luật tam giác.
3. Trung điểm của đoạn thẳng kết nối từ trực tâm đến đỉnh tam giác - Các trung điểm này cũng nằm trên đường tròn Euler. Chúng ta có thể sử dụng tính chất của các trung điểm và đường tròn Euler để chứng minh các tính chất của tam giác.
Vì vậy, đường tròn Euler cung cấp một khung cơ bản giúp chúng ta tính toán và chứng minh các tính chất của tam giác một cách dễ dàng và logic.
Liệu có tồn tại tam giác không có đường tròn Euler?
The Google search results suggest that there is a concept called \"đường tròn Euler\" in geometry, which is widely used in triangle problems.
In order to determine whether a triangle can exist without an Euler circle, we need to understand the conditions for the existence of an Euler circle.
The Euler circle of a triangle is a circle that passes through the triangle\'s orthocenter, centroid, and circumcenter.
To prove the existence of an Euler circle, we need to prove that the orthocenter, centroid, and circumcenter lie on the same line.
The orthocenter is the intersection point of the triangle\'s altitudes, which are the perpendiculars drawn from each vertex to the opposite side.
The centroid is the intersection point of the triangle\'s medians, which are the line segments connecting each vertex to the midpoint of the opposite side.
The circumcenter is the center of the circle that passes through all three vertices of the triangle.
If these three points are collinear, then it implies the existence of an Euler circle.
However, if these three points do not lie on the same line, then it means that there is no Euler circle for the triangle.
Therefore, to determine whether a triangle can exist without an Euler circle, we need to check if the orthocenter, centroid, and circumcenter are collinear. If they are collinear, then the triangle has an Euler circle; otherwise, it does not.

Nếu cạnh của tam giác là số chẵn, liệu đường tròn Euler có thể tồn tại?
Để chứng minh xem liệu đường tròn Euler có thể tồn tại trong tam giác có cạnh là số chẵn hay không, ta cần lưu ý đến một số khái niệm cơ bản về tam giác và đường tròn Euler.
1. Đường tròn Euler (hay còn gọi là đường tròn Ốle) là một đường tròn đi qua các điểm quan trọng trong một tam giác, bao gồm trực tâm (giao điểm của các đường cao), trọng tâm (giao điểm của các đường trung tuyến) và tâm đường tròn ngoại tiếp (giao điểm của các đường phân giác góc).
2. Một tam giác thông thường có thể có một đường tròn Euler. Tuy nhiên, không phải tất cả các tam giác đều có đường tròn Euler.
3. Để tồn tại một đường tròn Euler trong một tam giác, tổng số cạnh phải là số lẻ. Điều này có nghĩa là tam giác phải có 3 hoặc 1 cạnh.
Vì vậy, nếu cạnh của tam giác là số chẵn, không có đường tròn Euler có thể tồn tại.
Tóm lại, nếu tam giác có cạnh là số chẵn, không thể tồn tại đường tròn Euler.
_HOOK_
Toán 9 | Hình 6 : Tiếp tuyến của đường tròn, chứng minh tiếp tuyến đường tròn
Tiếp tuyến đường tròn là một khái niệm hình học thú vị. Video này sẽ giúp bạn hiểu cách xác định điểm tiếp xúc giữa đường thẳng và đường tròn, và cách tính toán tiếp tuyến của một đường tròn. Đừng bỏ lỡ cơ hội này để nắm bắt kiến thức mới!