Chủ đề tâm đường tròn ngoại tiếp tam giác đều: Tâm của đường tròn ngoại tiếp tam giác đều là một điểm đặc biệt, mang đến tính chất đẹp và thu hút trong tam giác đều. Điểm này nằm ở giao điểm của 3 đường trung trực của tam giác, tạo nên một sự đồng đều và cân đối. Tam giác đều là một hình học đẹp và hoàn hảo, và tâm của đường tròn ngoại tiếp mang đến sự độc đáo và nổi bật cho tam giác này.
Tìm công thức tính tâm của đường tròn ngoại tiếp tam giác đều?
Để tính tâm của đường tròn ngoại tiếp tam giác đều (tam giác có cả 3 cạnh bằng nhau), chúng ta có thể làm như sau:
Bước 1: Vẽ tam giác đều ABC với cạnh bằng nhau.
Bước 2: Vẽ các đường trung trực của ba cạnh AB, AC và BC.
Bước 3: Tìm giao điểm của ba đường trung trực, đây chính là tâm của đường tròn ngoại tiếp tam giác đều.
Bước 4: Đánh dấu tâm này là O.
Bước 5: Dùng thước vẽ, vẽ đường tròn đi qua ba đỉnh A, B và C để kiểm tra xem đó có phải là đường tròn ngoại tiếp không. Nếu đường tròn này đi qua ba đỉnh, tức là O là tâm của đường tròn ngoại tiếp tam giác đều.
Chú ý: Đường tròn ngoại tiếp tam giác là đường tròn tiếp xúc với các đỉnh của tam giác. Trong trường hợp tam giác đều, tâm của đường tròn ngoại tiếp cũng là tâm của tam giác.
Chú ý khác: Đừng quên kiểm tra lại kết quả bằng cách vẽ đường tròn đi qua ba đỉnh của tam giác để đảm bảo rằng đường tròn đúng là ngoại tiếp tam giác.
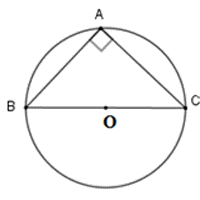
Định nghĩa tâm đường tròn ngoại tiếp tam giác đều là gì?
Định nghĩa \"tâm đường tròn ngoại tiếp tam giác đều\" là điểm trùng điểm giữa tâm và trung điểm của một cạnh của tam giác đều. Để tạo ra đường tròn ngoại tiếp tam giác đều, vẽ đường tròn có tâm là trung điểm của một trong các cạnh và bán kính bằng độ dài từ tâm đến một đỉnh của tam giác đều.
Làm thế nào để xác định vị trí của tâm đường tròn ngoại tiếp tam giác đều?
Để xác định vị trí của tâm đường tròn ngoại tiếp tam giác đều, ta cần làm như sau:
1. Vẽ tam giác đều ABC, trong đó ba đỉnh A, B, C cách đều nhau trên mặt phẳng.
2. Xác định tâm đường tròn ngoại tiếp của tam giác đều ABC bằng cách lấy giao điểm của ba đường trung trực của tam giác này. Đường trung trực của một cạnh tam giác là đoạn thẳng được vẽ từ trung điểm của cạnh đó đến đỉnh tam giác không nằm trên cạnh đó.
3. Gọi O là tâm đường tròn ngoại tiếp tam giác đều ABC.
4. Xác định tọa độ của các đỉnh A, B, C và góc quay tương ứng của đường trung trực AB, BC, CA.
5. Sử dụng công thức quay để tính toán tọa độ của tâm đường tròn ngoại tiếp O. Công thức quay có thể dùng để xoay điểm nằm trên mặt phẳng theo góc quay và tâm xoay.
6. Xác định tọa độ của tâm đường tròn ngoại tiếp tam giác đều ABC thông qua việc tính toán sử dụng công thức quay và tọa độ của các đỉnh A, B, C.
Tóm lại, để xác định vị trí của tâm đường tròn ngoại tiếp tam giác đều, ta cần xác định giao điểm của ba đường trung trực và tính toán tọa độ của tâm đường tròn ngoại tiếp thông qua công thức quay và tọa độ của các đỉnh tam giác.
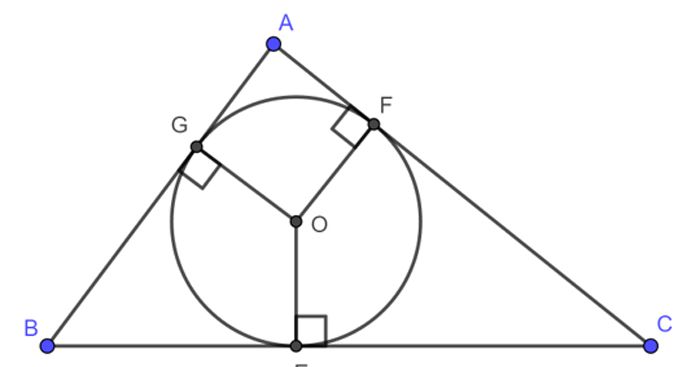
Đường tròn ngoại tiếp, đường tròn nội tiếp - Bài 8 - Toán học 9 - Cô Vương Thị Hạnh (DỄ HIỂU NHẤT)
Đường tròn nội tiếp: Để hiểu được các đường tròn nội tiếp và phân tích những tính chất thú vị của chúng, hãy xem video này ngay! Sẽ có những khám phá đáng ngạc nhiên đang chờ bạn khám phá.
Tâm của đường tròn ngoại tiếp tam giác đều có đặc điểm gì?
Để tìm tâm của đường tròn ngoại tiếp tam giác đều, ta cần biết đặc điểm của tam giác đều trước tiên. Tam giác đều có các cạnh bằng nhau và các góc bằng nhau, mỗi góc đều là 60 độ.
Để tìm tâm của đường tròn ngoại tiếp tam giác đều, ta thực hiện các bước sau:
Bước 1: Vẽ tam giác đều ABC.
Bước 2: Vẽ hai đường trung trực làm giao nhau tại một điểm gọi là O. Điểm O này là tâm của đường tròn ngoại tiếp tam giác đều ABC.
Bước 3: Vẽ các đường từ tâm O đến các đỉnh A, B và C. Ba đường này là bán kính của đường tròn ngoại tiếp tam giác và đều có độ dài bằng nhau.
Vậy, tâm của đường tròn ngoại tiếp tam giác đều là điểm giao nhau của hai đường trung trực và là trung điểm của các đường từ tâm đến các đỉnh của tam giác.
Hy vọng câu trả lời này giúp bạn hiểu rõ hơn về đặc điểm của tâm đường tròn ngoại tiếp tam giác đều.
Làm thế nào để tìm tọa độ của tâm đường tròn ngoại tiếp tam giác đều trên mặt phẳng?
Để tìm tọa độ của tâm đường tròn ngoại tiếp tam giác đều trên mặt phẳng, ta cần làm như sau:
Bước 1: Xác định tọa độ của ba đỉnh của tam giác đều. Giả sử ba đỉnh của tam giác đều là A(x1, y1), B(x2, y2), và C(x3, y3).
Bước 2: Tính tọa độ của tọa độ của tâm tam giác đều. Tọa độ tâm tam giác đều là trung điểm của các tọa độ đỉnh. Do tam giác đều có ba đỉnh có cùng khoảng cách với tâm, nên tọa độ tâm tam giác đều chính là trung bình cộng của các tọa độ đỉnh. Ta có công thức tính tọa độ tâm tam giác đều như sau:
Tâm tam giác đều có tọa đồ (xT, yT) với:
xT = (x1 + x2 + x3) / 3
yT = (y1 + y2 + y3) / 3
Làm theo các bước trên, ta sẽ tìm được tọa độ của tâm đường tròn ngoại tiếp tam giác đều trên mặt phẳng.
_HOOK_
Tại sao tâm đường tròn ngoại tiếp tam giác đều cũng là giao điểm của 3 đường trung trực của tam giác?
Tâm của đường tròn ngoại tiếp tam giác đều cũng là giao điểm của 3 đường trung trực của tam giác vì các đường trung trực này đều đi qua tâm đường tròn ngoại tiếp. Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó và vuông góc với đoạn thẳng đó.
Giả sử tam giác đều ABC có độ dài các cạnh đều bằng nhau và tâm của đường tròn ngoại tiếp là O. Để chứng minh tâm O cũng là giao điểm của 3 đường trung trực của tam giác, ta cần chứng minh rằng O nằm trên đường trung trực của mỗi cạnh của tam giác.
Đầu tiên, xét cạnh AB. Gọi I là trung điểm của cạnh AB, ta cần chứng minh rằng O nằm trên đường trung trực của AB, tức là OI vuông góc với AB.
Vì O nằm trên đường tròn ngoại tiếp tam giác đều ABC, nên AO = BO = CO = AB/2 = BC/2 = AC/2. Từ đó, ta có tam giác AOB cân và tam giác BOC cân. Suy ra, góc AOB = góc BOC = 60 độ.
Bây giờ, để chứng minh góc OIA = 90 độ, ta chia trường hợp:
- Trường hợp 1: I nằm trong tam giác ABC. Khi đó, ta có góc ABC bằng 60 độ và góc BAC bằng 30 độ. Do đó, góc OIA = góc ABC/2 + góc BAC/2 = 60 độ/2 + 30 độ/2 = 45 độ.
- Trường hợp 2: I nằm ngoài tam giác ABC. Khi đó, ta có góc ABC bằng 180 độ - 60 độ = 120 độ và góc BAC bằng 360 độ - 120 độ = 240 độ. Do đó, góc OIA = góc ABC/2 + góc BAC/2 = 120 độ/2 + 240 độ/2 = 180 độ.
Từ cả 2 trường hợp trên, ta đều được góc OIA = 90 độ, tức là OI vuông góc với AB. Tương tự, ta có thể chứng minh O nằm trên đường trung trực của các cạnh còn lại BC và AC bằng cách sử dụng cùng các tính chất của tam giác đều.
Vì vậy, tâm của đường tròn ngoại tiếp tam giác đều cũng là giao điểm của 3 đường trung trực của tam giác.
Có bao nhiêu đường trung trực trong tam giác và vì sao chúng đồng quy tại một điểm?
Trong tam giác, có tồn tại ba đường trung trực, mỗi đường trung trực là đường thẳng đi qua một đỉnh của tam giác và vuông góc với đoạn thẳng nối đỉnh đó với trung điểm của cạnh đối diện.
Để chứng minh rằng ba đường trung trực tam giác đồng quy tại một điểm, ta có thể sử dụng định lí trung điểm.
Đầu tiên, gọi ABC là một tam giác và I, II\' và III\' lần lượt là trung điểm của các cạnh BC, AC và AB.
Giả sử ta có 2 đường trung trực IA và II\' và chứng minh rằng chúng đồng quy tại một điểm.
Gọi M là giao điểm của IA và II\'.
Theo định lí trung điểm, ta có IM là đường trung trực của đoạn thẳng AC.
Ta cũng có II\' là đường trung trực của đoạn thẳng AC.
Vì vậy, hai đường trung trực IA và II\' đồng quy tại điểm M.
Tương tự, ta có thể chứng minh rằng ba đường trung trực tam giác đồng quy tại một điểm.
Do đó, trong tam giác, ba đường trung trực đồng quy tại một điểm gọi là trung điểm trong tam giác.
Tính chất của đường trung trực tam giác ở tam giác cân, tam giác đều, tam giác vuông và tam giác thường khác nhau như thế nào?
Tính chất của đường trung trực tam giác thay đổi tùy thuộc vào loại tam giác đó. Dưới đây là sự khác nhau giữa các loại tam giác:
1. Tam giác cân: Đường trung trực của một tam giác cân là đường thẳng đi qua đỉnh và giao điểm của đường trung trực chính giữa các cạnh. Điểm giao điểm này cách đỉnh một khoảng bằng một nửa đáy của tam giác.
2. Tam giác đều: Đường trung trực của một tam giác đều là các đường thẳng đi qua các đỉnh và giao nhau tại tâm của tam giác. Đường trung trực này chia đôi các góc của tam giác và đồng thời cắt các cạnh tại các điểm chính giữa.
3. Tam giác vuông: Đường trung trực của một tam giác vuông là các đường thẳng đi qua các đỉnh và giao nhau tại trung điểm của cạnh huyền. Đường trung trực của cạnh huyền cắt góc vuông thành hai góc bằng nhau.
4. Tam giác thường: Đường trung trực của một tam giác thường là các đường thẳng đi qua các đỉnh và giao nhau tại một điểm nằm bên trong tam giác.
Tóm lại, tính chất của đường trung trực tam giác thay đổi tùy thuộc vào loại tam giác và cách chúng tương tác với các điểm và cạnh của tam giác.
Tam giác đều và tam giác cân có cùng tâm đường tròn ngoại tiếp không? Vì sao?
Tam giác đều và tam giác cân không có cùng tâm đường tròn ngoại tiếp.
Để hiểu được điều này, ta cần biết rằng tâm đường tròn ngoại tiếp tam giác là điểm trùng với giao điểm của 3 đường trung trực của tam giác.
Trong tam giác cân, đường trung trực của cạnh đáy chính là đường trung trực kẻ từ đỉnh. Vì tam giác cân có 2 cạnh bằng nhau, nên đường trung trực của cạnh đáy cũng là đường trung trực của cạnh bên còn lại. Do đó, 3 đường trung trực của tam giác cân đồng quy tại một điểm, và đó chính là tâm đường tròn ngoại tiếp tam giác cân.
Tuy nhiên, trong tam giác đều, các cạnh đều có độ dài bằng nhau. Vì vậy, đường trung trực của mỗi cạnh là đường thẳng đi qua tâm tam giác và điểm trung điểm của cạnh đó. Vì các cạnh trong tam giác đều đều có một đường trung trực, nên ta có 3 đường trung trực đồng quy tại một điểm. Điểm đó chính là tâm đường tròn ngoại tiếp tam giác đều.
Vậy nên, tam giác đều và tam giác cân không có cùng tâm đường tròn ngoại tiếp, vì đồng quy của các đường trung trực trong tam giác đều khác với đồng quy của các đường trung trực trong tam giác cân.

Những tứ giác có tâm đường tròn ngoại tiếp tam giác đều là những tứ giác nào?
Những tứ giác có tâm đường tròn ngoại tiếp tam giác đều được gọi là tứ giác nội tiếp hoặc tứ giác tiếp điểm. Tứ giác nội tiếp là những tứ giác có tất cả các đỉnh đều nằm trên một đường tròn.
Trong trường hợp của tam giác đều, mỗi cạnh của tam giác đều có tâm đường tròn ngoại tiếp là tâm của tam giác đó. Vì tam giác đều có ba cạnh và ba tâm đường tròn ngoại tiếp là như nhau nên tất cả các tứ giác có tâm đường tròn ngoại tiếp tam giác đều là tứ giác nội tiếp.
Ví dụ, hình bình hành, hình chữ nhật, hình vuông, và hình thang cân đều là những tứ giác có tâm đường tròn ngoại tiếp tam giác đều. Tuy nhiên, không tất cả các tứ giác nội tiếp đều là tứ giác có tâm đường tròn ngoại tiếp tam giác đều.
_HOOK_