Lý thuyết Hệ thức Vi-ét và ứng dụng hay nhất

By Admin 29/03/2024 0

1.Hệ thức Vi-ét

Cho phương trình bậc hai 

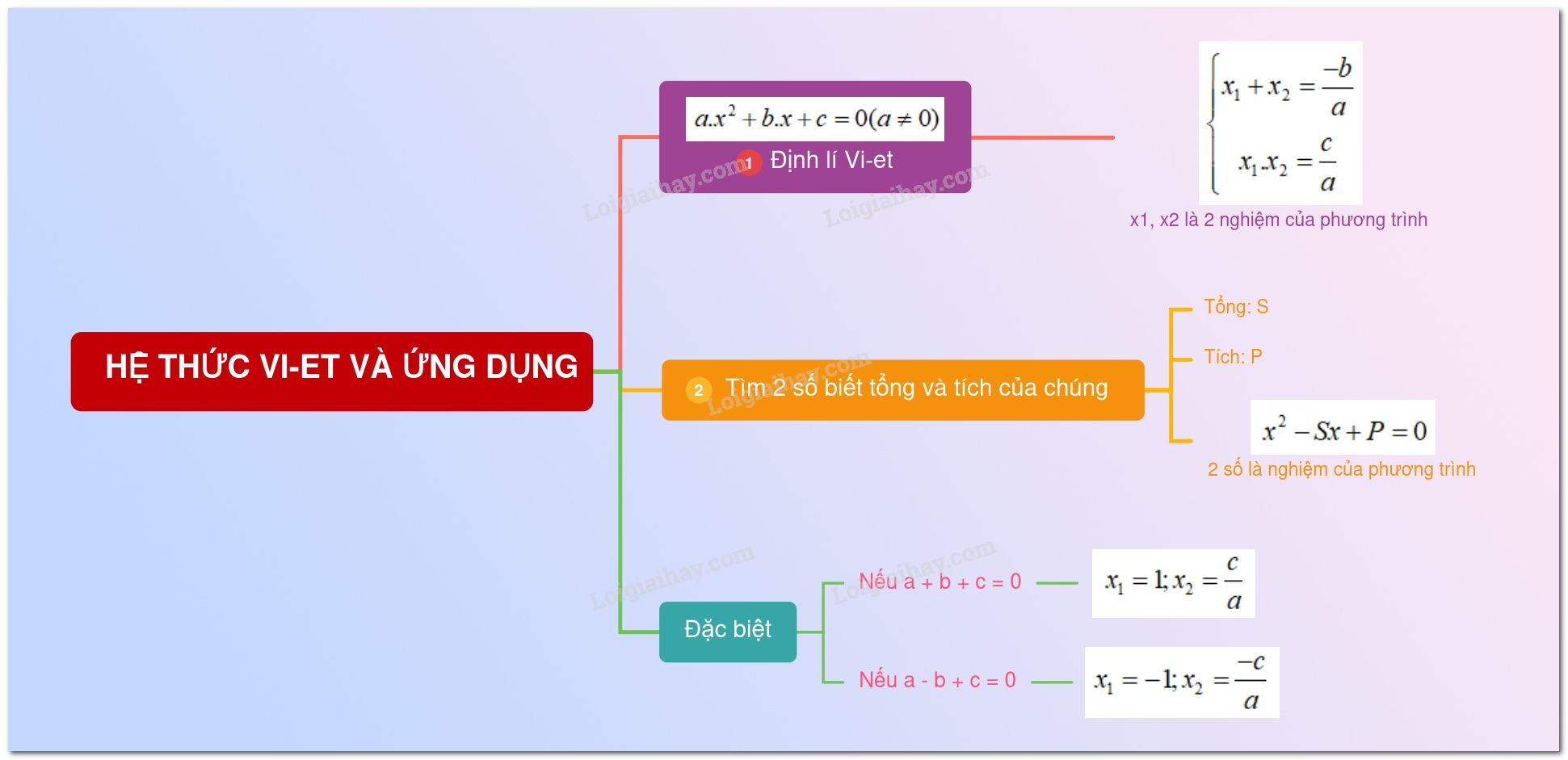
ax² + bx + c = 0 (a ≠ 0) 

Bạn đang xem: Lý thuyết Hệ thức Vi-ét và ứng dụng hay nhất

Nếu là nhị nghiệm của phương trình bên trên thì:

Lý thuyết Hệ thức Vi-ét và phần mềm. | SGK Toán lớp 9

2.Ứng dụng của hệ thức Vi-ét

#1. Dùng hệ thức Vi-ét nhằm tính nhẩm nghiệm những phương trình dạng quánh biệt

Xét phương trình bậc nhị ax² + bx + c = 0 (a ≠ 0).

Nếu a + b + c = 0 thì phương trình với 1 nghiệm là x = 1 và nghiệm sót lại là x = c/a.

Nếu a – b + c = 0 thì phương trình với 1 nghiệm là x = -1 và nghiệm sót lại là x = -c/a.

Cho phương trình x² + 3x − 4 = 0.

Ta thấy a = 1, b = 3 và c = −4 nên a + b + c = 1 + 3 − 4 = 0

Vậy phương trình tiếp tục mang lại với nghiệm x = 1 và x = c/a = − 4/1 = − 4.

Giải phương trình 5x² + 7x + 2 = 0.

Ta thấy rằng a = 5, b = 7 và c = 2 nên a − b + c = 5 − 7 + 2 = 0.

Vậy tao suy rời khỏi ngay lập tức phương trình tiếp tục mang lại với nghiệm x = −1 và x = − c/a = − 2/5.

Như vậy phần mềm hệ thức Vi-ét tạo điều kiện cho ta tính nhẩm nghiệm những phương trình có

a + b + c = 0 và a − b + c = 0.

#2. Tìm nhị số biết tổng và tích của chúng

Nếu nhị số với tổng vị S và tích vị P.. thì nhị số này đó là nhị nghiệm của phương trình:

X² − SX+ P.. = 0

Tìm nhị số u và v biết u + v = 15 và u.v = 36.

Giải.

Ta giải phương trình X² − SX+ P.. = 0 với S = 15 và P.. = 36.

Ta với pt sau:

X² − 15X+ 36 = 0

Giải phương trình bậc hai này, tao có: X = 12 hoặc X = 3.

Vậy u = 12 và v = 3 hoặc u = 3 và v = 15.

#3. Xét vết những nghiệm của phương trình bậc hai

Ta hiểu được phương trình bậc nhị với nhị nghiệm phân biệt ⇔ Δ > 0.

Phương trình bậc nhị với nhị nghiệm ⇔ Δ ≥ 0.

Giờ tao với những tình huống xét vết những nghiệm của pt bậc nhị như sau:

Sau phía trên tao tiếp tục giải một vài ba ví dụ ví dụ nhằm vận dụng hệ thức Vi-ét nhằm xét vết những nghiệm của phương trình bậc nhị. Các bài bác luyện dạng này thông thường được thêm thông số m.

Bạn cần lưu ý rằng x là ẩn, còn m là thông số.

Cho phương trình

x² − 2(m − 3)x + 8 − 4m = 0 (1)

Tìm những độ quý hiếm của thông số m nhằm phương trình có 

  1. a) Có nhị nghiệm trái khoáy dấu
  2. b) Có nhị nghiệm phân biệt nằm trong âm
  3. c) Có đích thị một nghiệm dương

Hướng dẫn giải:

  1. a) Ta với a = 1 và c = 8 − 4m.

Phương trình (1) với nhị nghiệm trái khoáy vết ⇔ ac 0 

⇔ 1. (8 − 4m) 0

⇔ 8 − 4m 0

⇔ 4m > 8

⇔ m > 2

  1. b) Phương trình (1) với nhị nghiệm phân biệt cùng cách nói ⇔ Δ’ > 0, P.. > 0, S 0

Δ’ > 0 ⇔  (m – 3)² – (8 – 4m) > 0

⇔ m² – 6m + 9 – 8 + 4m > 0

⇔ m² – 2m + 1 > 0

⇔ (m – 1)² > 0 ⇔ m ≠ 1 ( vì thế (m – 1)² ≥ 0 với từng m)

Theo hệ thức Vi-ét, tao với P.. = 8 – 4m

P > 0 ⇔  8 − 4m > 0 ⇔ 4m 8 ⇔  m 2

S 0 ⇔  2(m – 3) 0 ⇔ m – 3 0 ⇔  m 3

Vậy m 2 và m ≠ 1 thì phương trình (1) với nhị nghiệm phân biệt cùng cách nói.

  1. c) Phương trình có một nghiệm dương tao rất có thể hiểu theo đòi 2 ngôi trường hợp:

TH1: Phương trình với nghiệm kép là nghiệm dương.

TH2: Phương trình với nhị nghiệm trái khoáy vết thì tiếp tục có một nghiệm dương.

Ta giải 2 tình huống như sau:

TH1: Xét Δ’ = (m – 1)² = 0 ⇔ m = 1.
Khi cơ tao thay cho vô pt được:

x² + 4x  + 4 = 0 ⇔ (x + 2)² = 0 ⇔ x = -2 0 => loại

TH2: Pt (1) với 2 nghiệm trái khoáy vết thì tiếp tục có một nghiệm dương nên kể từ câu a tao có:

m > 2.

Xem thêm:

Chuyên đề Ôn ganh đua vô lớp 10 môn Toán

Xem thêm: Tờ khai hải quan tiếng Anh

Cho phương trình

x² – 2(m + 2)x +4m = 0.

  1. a) Chứng minh rằng phương trình (1) luôn luôn với nhị nghiệm phân biệt với từng độ quý hiếm của m.
  2. b) Tìm một hệ thức contact thân thuộc nhị nghiệm của phương trình (1) ko tùy theo m.

Hướng dẫn giải:

  1. a) Xét biệt thức Δ’ = b’² − ac = (m + 2)² − 4m = m² + 4 > 0 với từng độ quý hiếm của m.

Vậy phương trình (1) luôn luôn với 2 nghiệm phân biệt với từng độ quý hiếm của m.

  1. b) Theo hệ thức Vi-ét, tao có:

Để viết lách được một hệ thức contact thân thuộc nhị nghiệm ko tùy theo m tao tuân theo nhị bước:

Bước 1: Theo hệ thức Vi-ét viết lách tổng và tích nhị nghiệm theo đòi m.

Bước 2: Dùng quy tắc nằm trong hoặc thế nhằm khử m.

Ở hệ thức bên trên tao thấy nếu như nhân 2 vô tổng thì được 4m + 4 rồi trừ lên đường tích tiếp tục mất mặt 4m.

Suy ra 

Vậy là biểu thức bên trên không hề dựa vào m.

#4. Tìm m nhằm phương trình bậc nhị với nhị nghiệm vừa lòng hệ thức mang lại trước

Tiếp theo đòi đấy là một ví dụ về vận dụng hệ thức Vi-ét nhằm trình diễn biểu thức theo đòi nhị nghiệm của phương trình tiếp tục mang lại.

Trước tiên những em cần phải biết cơ hội biến hóa biểu thức đối xứng theo đòi tổng và tích nhằm vận dụng hệ thức Vi-ét.

Ta tiếp tục tiến hành quá trình sau:

Bước 1: Tìm ĐK nhằm phương trình với nghiệm. Từ cơ vận dụng hệ thức Vi-ét.

Bước 2: Biến thay đổi biểu thức theo đòi tổng và tích nhị nghiệm rồi người sử dụng hệ thức Vi-ét viết lách ở bước 1.

Một số biểu thức đối xứng trong số những nghiệm thông thường gặp:

Tuy nhiên, với đề bài bác tiếp tục đòi hỏi trình diễn những biểu thức ko đối xứng.

Như ví dụ sau đây.

Cho phương trình

x² − 2mx − 4m − 5 = 0 (1) 

  1. a) Giải phương trình (1) khi m = – 2.
  2. b) Chứng minh phương trình (1) luôn luôn với nghiệm với từng độ quý hiếm của m.
  3. c) Gọi là nhị nghiệm của phương trình (1). Tìm m để:

Hướng dẫn giải:

  1. a) Với dạng này, tao thay cho m = -2 vô phương trình (1) rồi giải phương trình bậc nhị, tao có:

x² + 4x +3 = 0 ⇔ (x + 3)(x + 1) = 0 ⇔ x = -3 hoặc x = -1.

Vậy với m = -2 thì phương trình (1) với luyện nghiệm là: S = {-3, -1}.

  1. b) Muốn minh chứng pt (1) luôn luôn với nghiệm với từng m tao cần chỉ ra rằng Δ hoặc Δ’ > 0 với từng m.

Ta có:

Δ’ = m² – (-4m – 5) = m² + 4m + 5 = (m + 2)² +1 > 0 với từng m.

Do cơ phương trình (1) luôn luôn với nhị nghiệm với từng độ quý hiếm của m.

  1. c) Do phương trình (1) luôn luôn với nhị nghiệm với từng m, nên tao gọi nhị nghiệm của phương trình (1) là

Theo hệ thức Vi-ét tao có:

Ta có:

Do là nghiệm của (1) nên 

Ta có:

⇔ 2.2m = 1524000

⇔  m = 381000

Vậy m = 381000 thì vừa lòng đòi hỏi đề bài bác.

Cho phương trình

x² – 2mx +2m – 1 = 0

a) Chứng minh phương trình luôn luôn với nghiệm với từng độ quý hiếm của m.

Muốn minh chứng phương trình luôn luôn với nghiệm tao chỉ ra rằng Δ ≥ 0 (hoặc Δ’ ≥ 0).

b) Tìm m nhằm phương trình với nhị nghiệm thỏa mãn

Hướng dẫn:

Áp dụng hệ thức Vi-ét tao có:

Ta có: 

Vậy m = 3/2 hoặc m = -1/2 thì vừa lòng đòi hỏi đề bài bác.

Cho phương trình

x² – 6x + m = 0

Tìm độ quý hiếm của m nhằm phương trình bên trên với nhị nghiệm vừa lòng điều kiện

Hướng dẫn giải:

Theo hệ thức Vi-ét tao có:

Ta kết phù hợp với điều kiện 

Ta giải hệ phương trình:

Vì nên m = 8. (-2) = -16.

Vậy m = -16 thì vừa lòng đòi hỏi đề bài bác.

3.Mọi người cũng hỏi

Lý thuyết hệ thức Vi-ét là gì?

Lý thuyết hệ thức Vi-ét là một trong nghành nghề vô đại số, phân tích về hệ thức và bất đẳng thức nhiều trở thành và tác dụng của bọn chúng. Nó được mệnh danh theo đòi căn nhà toán học tập người Pháp, Alexandre-Théophile Vandermonde và Joseph-Louis Lagrange.

Xem thêm: %C4%90%C3%B4ng%20Nam%20%C3%81 trong Tiếng Anh, dịch

Hệ thức và bất đẳng thức là những định nghĩa chủ yếu vô lý thuyết hệ thức Vi-ét?

Đúng, hệ thức và bất đẳng thức là nhị định nghĩa đa phần vô lý thuyết hệ thức Vi-ét. Hệ thức là một trong phương trình với đựng được nhiều trở thành, còn bất đẳng thức là một trong mệnh đề đối chiếu độ quý hiếm của những biểu thức số học tập.

Lý thuyết hệ thức Vi-ét được phần mềm vô nghành nghề nào?

Lý thuyết hệ thức Vi-ét với phần mềm rộng thoải mái trong số nghành nghề như tối ưu hóa, tài chủ yếu, phần trăm và tổng hợp, cơ vật lý, nghệ thuật, và nhiều việc vô khoa học tập và technology.

Tại sao lý thuyết hệ thức Vi-ét cần thiết vô toán học tập và phần mềm của nó?

Lý thuyết hệ thức Vi-ét là một trong phần cần thiết vô đại số và với tầm quan trọng cần thiết vô giải quyết và xử lý những việc thực tiễn phức tạp. Các cách thức và nghệ thuật vô lý thuyết hệ thức Vi-ét canh ty tối ưu hóa những ra quyết định và giải quyết và xử lý những việc thực tiễn trong không ít nghành nghề không giống nhau.