Cho hình chóp đều (S.ABCD) có (AB = 2a,,,SA = 2asqrt 2 .) Góc giữa (SB) và mặt phẳng (left( {ABCD} right)) bằng:

Phương pháp giải:

Góc thân thiện đường thẳng liền mạch \(SB\) và mặt mày phẳng phiu \(\left( {ABCD} \right)\) là góc thân thiện \(SB\) và hình chiếu vuông góc của \(SB\) bên trên \(\left( {ABCD} \right).\)

Bạn đang xem: Cho hình chóp đều (S.ABCD) có (AB = 2a,,,SA = 2asqrt 2 .) Góc giữa (SB) và mặt phẳng (left( {ABCD} right)) bằng:

Lời giải chi tiết:

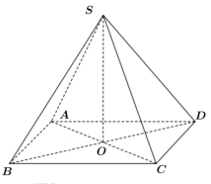
Gọi \(O\) là giao phó điểm của \(AC\) và \(BD.\)

\( \Rightarrow SO \bot \left( {ABCD} \right).\)

\( \Rightarrow OB\) là hình chiếu vuông góc của \(SB\) bên trên \(\left( {ABCD} \right).\)

Xem thêm: 40+ TỪ VỰNG VỀ MÙA ĐÔNG TRONG TIẾNG ANH CẦN "NOTE NGAY"

\( \Rightarrow \angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,OB} \right) = \angle SBO\)

Áp dụng ấn định lý Pitago mang đến \(\Delta ABD\) vuông bên trên \(A\) tớ có:

\(\begin{array}{l}BD = \sqrt {A{B^2} + A{D^2}}  = \sqrt {4{a^2} + 4{a^2}}  = 2a\sqrt 2 \\ \Rightarrow OB = \dfrac{1}{2}BD = a\sqrt 2 .\end{array}\)

Xem thêm: Chứng chỉ tiếng anh B1 có thời hạn bao lâu? [Cập nhật 2024]

Xét \(\Delta SBO\) vuông bên trên \(O\) tớ có: \(\cos SBO = \dfrac{{BO}}{{SB}} = \dfrac{{a\sqrt 2 }}{{2a\sqrt 2 }} = \dfrac{1}{2}\)\( \Rightarrow \angle SBO = {60^0}.\) 

Vậy \(\angle \left( {SB;\,\,\left( {ABCD} \right)} \right) = {60^0}.\)

Chọn C.