Lý thuyết phương trình mặt phẳng | SGK Toán lớp 12

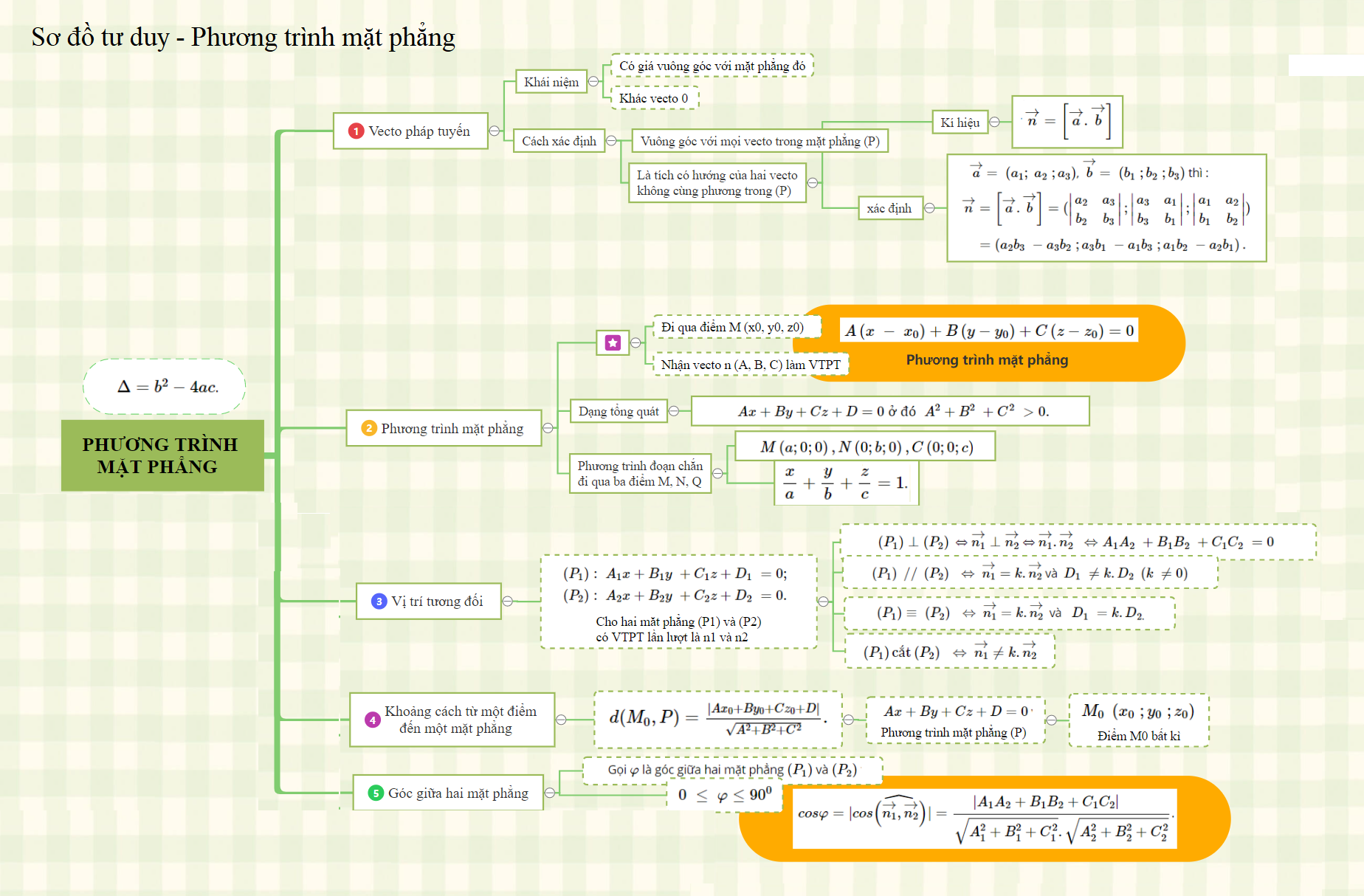
1. Vectơ pháp tuyến của mặt mũi phẳng lì.

* Cho mặt mũi phẳng lì \((P)\) , vectơ  \(\overrightarrow{n}\neq \overrightarrow{0}\) mà giá bán của chính nó vuông góc với mặt mũi phẳng lì \((P)\) thì \(\overrightarrow{n}\) được gọi là vectơ pháp tuyến của mặt mũi phẳng lì \((P)\).

Bạn đang xem: Lý thuyết phương trình mặt phẳng | SGK Toán lớp 12

* Cho mặt mũi phẳng lì \((P)\) , cặp vectơ  \(\overrightarrow{a}\neq \overrightarrow{0}\), \(\overrightarrow{b}\neq \overrightarrow{0}\) không nằm trong phương tuy nhiên giá bán của bọn chúng là hai tuyến phố trực tiếp tuy nhiên song hoặc trực thuộc mặt mũi phẳng lì \((P)\) được gọi là cặp vectơ chỉ phương của mặt mũi phẳng lì \((P)\). Khi bại vectơ \(\overrightarrow{n}=\left [\overrightarrow{a}.\overrightarrow{b} \right ]\). là vectơ pháp tuyến của mặt mũi phẳng lì \((P)\).

* Nếu \(\overrightarrow{a}\) \( = \;\left( {{a_1};{\rm{ }}\;{a_{2\;}};{\rm{ }}{a_3}} \right)\), \(\overrightarrow{b}\) \( = \;\left( {{b_1}\;;{\rm{ }}{b_2}\;;{\rm{ }}{b_3}} \right)\) thì :

         \(\overrightarrow{n}=\left [\overrightarrow{a}.\overrightarrow{b} \right ]=(\begin{vmatrix} a_{2}&a_{3} \\ b_{2}& b_{3} \end{vmatrix};\begin{vmatrix} a_{3} & a_{1}\\ b_{3}&b_{1} \end{vmatrix};\begin{vmatrix} a_{1} & a_{2}\\ b_{1}& b_{2} \end{vmatrix})\)

               \( = \left( {{a_2}{b_3}\;-{\rm{ }}{a_3}{b_{2\;}};{\rm{ }}{a_3}{b_1}\;-{\rm{ }}{a_1}{b_3}\;;{\rm{ }}{a_1}{b_2}\;-{\rm{ }}{a_2}{b_1}} \right).\)

* Mặt phẳng lì trọn vẹn được xác lập lúc biết một điểm và một vectơ pháp tuyến của chính nó, hay như là 1 điểm nằm trong mặt mũi phẳng lì và cặp vectơ chỉ phương của chính nó.

2. Phương trình mặt mũi phẳng lì.

* Mặt phẳng lì  \((P)\) qua loa điểm \({M_{0\;}}\left( {{x_0}\;;{\rm{ }}{y_{0\;}};{\rm{ }}{z_0}} \right){\rm{ }}\;\) và nhận \(\overrightarrow{n}\) \(\left( {A,{\rm{ }}B,{\rm{ }}C} \right)\) thực hiện vectơ pháp tuyến đem phương trình đem dạng: \(A\left( {x\;-\;{x_0}} \right) + B\left( {y-{y_0}} \right) + C\left( {z-{z_0}} \right) = 0\)

* Mọi mặt mũi phẳng lì vô không khí đem phương trình tổng quát mắng đem dạng:

\(\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;{\rm{ }}\;Ax{\rm{ }} + {\rm{ }}By + Cz + D = 0{\rm{ }}\;{\rm{ }} \text {ở bại }\;{A^2} + {\rm{ }}{B^2}\; + {C^{2\;}} > 0.\) Khi bại vectơ \(\vec n\,(A;B;C)\) là vectơ pháp tuyến của mặt mũi phẳng lì.

* Mặt phẳng lì trải qua tía điểm \(M\left( {a;0;0} \right),{\rm{ }}N\left( {0;b;0} \right),{\rm{ }}C\left( {0;0;c} \right)\) ở bại \(abc\; \ne 0\) đem phương trình :\(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\). Phương trình này còn được gọi là phương trình mặt mũi phẳng lì bám theo đoạn chắn.

3. Vị trí kha khá của nhị mặt mũi phẳng lì.

 Cho nhị mặt mũi phẳng lì \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) đem phương trình :

\(\begin{array}{*{20}{l}}
{\left( {{P_1}} \right):\;{A_1}x + {B_1}y\; + {C_1}z + {D_1}\; = 0;}\\
{\left( {{P_2}} \right):\;{A_2}x + {B_2}y\; + {C_2}z + {D_2}\; = 0.}
\end{array}\)

Ta có \(\overrightarrow {{n_1}} \;(A1;B1;C1) \bot (P1)\) và \(\overrightarrow {{n_2}} \;(A2;B2;C2) \bot (P2)\). Khi đó:

Xem thêm: Bắt Chủ tịch HĐQT Tập đoàn Thái Dương vì bán trái phép hơn 11.000 tấn đất hiếm

 \(({P_1})\; \bot \;({P_2})\)  ⇔ \(\overrightarrow{n_{1}}\perp \overrightarrow{n_{2}}\) ⇔ \(\overrightarrow{n_{1}}.\overrightarrow{n_{2}}\)  \(\; \Leftrightarrow {\rm{ }}{A_1}{A_2}\; + {\rm{ }}{B_1}{B_2}\; + {\rm{ }}{C_1}{C_2}\; = {\rm{ }}0\)

  \(\left( {{P_1}} \right)\;//\;\left( {{P_2}} \right)\;\; \Leftrightarrow \;\) \(\overrightarrow{n_{1}}=k.\overrightarrow{n_{2}}\) và  \({D_1}\; \ne {\rm{ }}k.{D_2}\;\left( {k\; \ne {\rm{ }}0} \right).\)

  \(\left( {{P_1}} \right) \equiv \;\left( {{P_2}} \right)\;\; \Leftrightarrow \;\) \(\overrightarrow{n_{1}}=k.\overrightarrow{n_{2}}\)  và  \(\;{D_1}\; = {\rm{ }}k.{D_{2.}}\)

  \(\left( {{P_1}} \right) \text {cắt} \left( {{P_2}} \right)\;\; \Leftrightarrow \;\) \(\overrightarrow{n_{1}}\neq k.\overrightarrow{n_{2}}\) (nghĩa là \(\overrightarrow{n_{1}}\) và \(\overrightarrow{n_{2}}\) không nằm trong phương).

4. Khoảng cơ hội từ là 1 điểm đến lựa chọn một phía phẳng lì.

Trong không khí \(Oxyz\) mang lại mặt mũi phẳng lì \((P)\) đem phương trình:

             \(Ax + By + Cz +D = 0\) và điểm \({M_{0\;}}\left( {{x_0}\;;{\rm{ }}{y_{0\;}};{\rm{ }}{z_0}} \right).\) .Khoảng cơ hội từ M₀ đến \((P)\) được mang lại bởi vì công thức:

\(d({M_0},P) = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\)

5. Góc thân thuộc nhị  mặt phẳng lì.

Cho nhị mặt mũi phẳng lì \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\)  có phương trình :

\(\begin{array}{*{20}{l}}
{\left( {{P_1}} \right):\;{A_1}x + {B_1}y\; + {C_1}z + {D_1}\; = 0;}\\
{\left( {{P_2}} \right):\;{A_2}x + {B_2}y\; + {C_2}z + {D_2}\; = 0.}
\end{array}\)

Gọi \(\varphi \) là góc thân thuộc nhị mặt mũi phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) thì \(0\; \le \;\varphi {\rm{ }} \le {\rm{ }}{90^{0\;}}\) và :

Xem thêm: Thành lập công ty tiếng Anh là gì? Thuật ngữ tiếng Anh về đăng ký doanh nghiệp

\(cos\varphi =|cos\widehat{\left (\overrightarrow{n_{1}},\overrightarrow{n_{2}} \right )}|=\dfrac{|A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}.\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\).

Loigiaihay.com