
1. Công thức nghiệm:
Đối với phương trình có dạng ax² + bx + c = 0 (a ≠ 0)
Ta có biệt thức của phương trình là: Δ = b2 – 4ac
- Trường hợp 1: Nếu Δ > 0 thì ta có phương trình có 2 nghiệm phân biệt
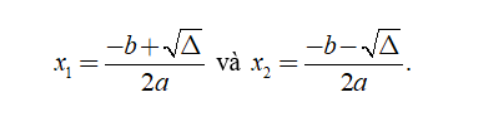
- Trường hợp 2: Nếu Δ = 0 thì ta có phương trình có nghiệm kép
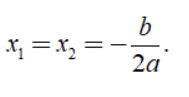
- Trường hợp 3: Nếu Δ < 0 thì ta có phương trình đã cho vô nghiệm
Lưu ý: Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có 2 ẩn a và c trái dấu, tức là ac < 0. Lúc này, ta có Δ = b² – 4ac > 0 ⇒ Phương trình luôn luôn có 2 nghiệm phân biệt
2. Định lý Viet của phương trình bậc 2
Khi gặp các phương trình bậc 2 hay giải phương trình bậc 2 một ẩn, các em học sinh không thể không nhắc tới định lý Viet. Đây là một trong những định lý quan trọng giúp các em dễ dàng giải quyết các dạng bài liên quan tới phương trình bậc 2
Ta có phương trình bậc 2 có dạng: ax² + bx + c = 0 (a ≠0) là phương trình có tối đa 2 nghiệm, gọi là x1 và x2. Khi đó, theo định lý Viet ta có mối liên hệ giữa các 2 nghiệm và các ẩn của phương trình như sau:
x1 + x2 = -b/a
x1x2 = c/a
Khi làm các dạng bài tập về phương trình bậc 2, các em học sinh có thể áp dụng mối liên hệ trên vào quá trình biến đổi biểu thức phương trình bậc 2 . Cụ thể như sau:
Bạn cũng có thể áp dụng định lý Viet đảo với 2 số x1 và x2 thỏa mãn 2 điều kiện:
- x1 + x2 = S
- x1x2 = P
Trong đó: cả x1 và x2 đều là nghiệm của phương trình x² – Sx + P = 0.
Ứng dụng của định lý Viet được áp dụng rất nhiều trong các dạng bài tập về phương trình bậc 2. Với phương trình bậc 2, các em học sinh hoàn toàn có thể dễ dàng tìm ra nghiệm của phương trình mà không cần dùng tới Δ trong một số trường hợp đặc biệt sau:
- Trường hợp 1: a+b+c=0 thì phương trình bậc 2 có 2 nghiệm là x1 = 1 và x2 = c/a.
- Trường hợp 2: a-b+c=0 thì phương trình bậc 2 2 nghiệm là x1 = -1 và x2 = -c/a. (Đây là trường hợp ngược lại với trường hợp 1, các em học sinh cần lưu ý kỹ để tránh bị nhầm lẫn trong quá trình làm bài)
B. Dạng bài tập ứng dụng công thức nghiệm của phương trình bậc 2
HOCMAI sẽ chia sẻ một số dạng bài tập thường gặp về phương trình bậc 2. Mỗi dạng bài sẽ có một phương pháp giải khác nhau, chính vì vậy, khi nắm vững được các dạng, áp dụng đúng cách và đúng phương pháp sẽ giúp các em học sinh tiết kiệm thời gian và có được đáp án chính xác nhất.
Dạng bài tập 1: Phương trình bậc 2 1 ẩn không có tham số
Khi gặp dạng bài tập này, các em học sinh chỉ cần cần áp dụng công thức tính Δ và Δ’ rồi áp dụng các công thức tính nghiệm phương trình bậc 2 như đã được giới thiệu ở trên. Từ đó tính ra các nghiệm của phương trình
Ví dụ: Tìm nghiệm của phương trình sau: x2 – 3x+2 = 0.
Áp dụng công thức tính Δ, ta sẽ có Δ = b2 – 4ac = 1.
Vậy nghiệm của phương trình trên lần lượt là:
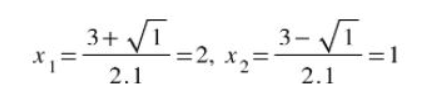
Dạng bài tập 2: phương trình bậc 2 có 1 ẩn là tham số
Bên cạnh dạng không chứa tham số, phương trình bậc 2 một ẩn có tham số cũng là một dạng bài tập quan trọng. Đây thường là những dạng bài tìm điều kiện để hàm số đã cho có 2 nghiệm, có 1 nghiệm hoặc tìm điều kiện để hàm số vô nghiệm.
Để làm được dạng bài tập này, các em học sinh cũng cần sử dụng công thức tính Δ. Sau đó, dựa các trường hợp của Δ để từ đó xét điều kiện như đề bài đưa ra.
Các trường hợp của Δ bao gồm có:
- Nếu Δ > 0 thì ta có phương trình có 2 nghiệm phân biệt
- Nếu Δ < 0 thì ta có phương trình vô nghiệm
- Nếu Δ = 0 thì ta có phương trình có 1 nghiệm (hoặc 2 nghiệm trùng nhau)
C. Các dạng bài thường gặp phương trình bậc 2
Bài tập luyện tập
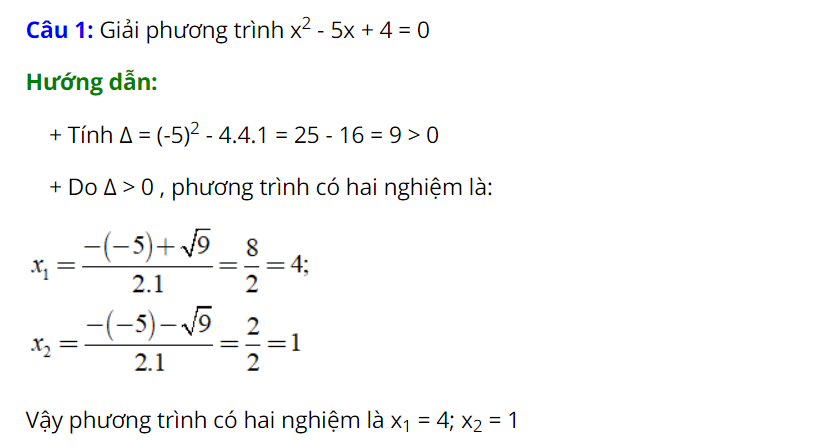

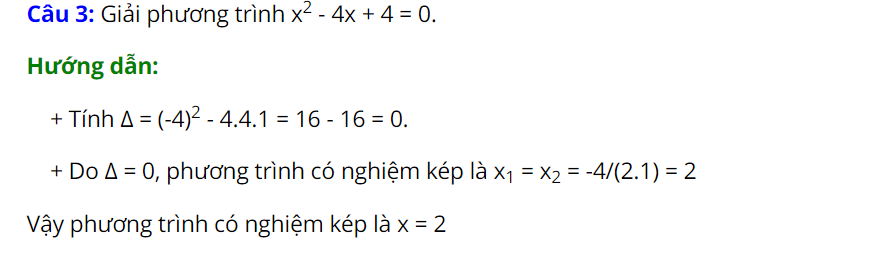
Bài tập thực hành
![]()
Hướng dẫn giải

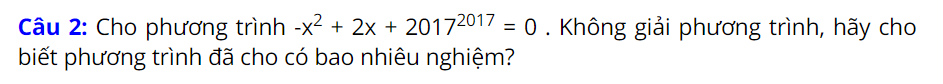
Hướng dẫn giải

Tham khảo thêm:
Cách giải phương trình bậc 2
Phương trình bậc 2 một ẩn
Trên đây là toàn bộ kiến thức cần nắm được về công thức nghiệm của phương trình bậc 2 thuộc chương trình toán lớp 9. Hy vọng với bài viết trên sẽ giúp các em học sinh có thêm kiến thức hữu ích trong quá trình làm bài tập cũng như ôn thi Toán vào lớp 10 trong thời gian tới.











