Công thức tính diện tích tam giác vuông, cân, đều đầy đủ, chi tiết

Công thức tính diện tích S tam giác thường, vuông và cân nặng là những kiến thức và kỹ năng cơ phiên bản vô toán học tập lớp 8. Dưới phía trên, VOH Giáo dục đào tạo tổ hợp những công thức dễ nắm bắt và được dùng thịnh hành nhằm tính diện tích S tam giác chung những em học viên dễ dàng và đơn giản ghi lưu giữ và phần mềm giải bài bác luyện toán.

1. Định nghĩa tam giác và những mô hình tam giác

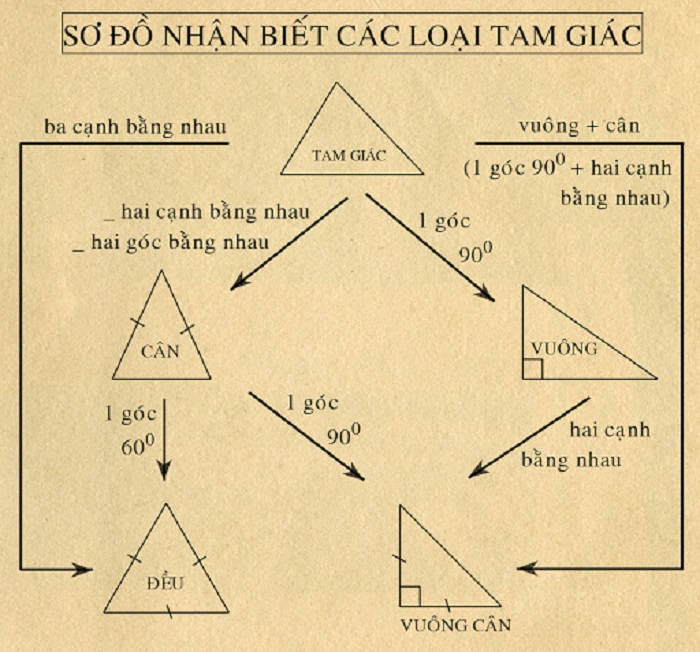
Hình tam giác là hình với 3 điểm, 3 cạnh, 3 góc và tổng 3 góc vày 180 chừng. Có những mô hình tam giác sau:

Bạn đang xem: Công thức tính diện tích tam giác vuông, cân, đều đầy đủ, chi tiết

• Tam giác thường: Là tam giác với số đo những cạnh và những góc không giống nhau.
• Tam giác cân: Là tam giác với nhì cạnh và nhì góc đều bằng nhau.
• Tam giác đều: Là tam giác với tất cả tía cạnh và tía góc đều bằng nhau, đó là tình huống quan trọng của tam giác cân nặng.
• Tam giác vuông: Là tam giác với cùng một góc bất kì vày 90 chừng, góc này được gọi là góc vuông. Các cạnh vô tam giác vuông bao hàm cạnh huyền đối lập góc vuông và nhì cạnh kề góc vuông.
• Tam giác tù: Là tam giác với cùng một góc vô to hơn 90 chừng.
• Tam giác nhọn: Là tam giác với tía góc vô đều nhỏ rộng lớn 90 chừng.

2. Tổng phù hợp những công thức tính diện tích S tam giác

Thông thông thường diện tích tam giác sẽ tiến hành tính vày ½ tích của độ cao hạ kể từ đỉnh với chừng lâu năm của cạnh lòng (tức là cạnh đối lập của đỉnh đó).

S = một nửa a.h

Trong đó:

• h là độ cao hạ kể từ đỉnh xuống cạnh đáy
• a là chiều lâu năm cạnh đáy
• S là diện tích

Lưu ý: Với độ cao hạ kể từ đỉnh sẽ sở hữu 2 tình huống xẩy ra là độ cao ở phía vô và độ cao ở phía ngoài của tam giác (tam giác tù).

2.1. Công thức tính diện tích S tam giác lúc biết 3 cạnh

Nếu cho thấy thêm 3 cạnh của tam giác và đòi hỏi tính diện tích S của tam giác, những chúng ta cũng có thể vận dụng một vài công thức sau:

S = 1/2(a+b+c)(a+b-c)(b+c-a)(c+a-b)

Trong đó: a, b, c là chừng lâu năm của 3 cạnh với vô tam giác

Hoặc những chúng ta cũng có thể vận dụng công thức Heron:

S= (p(p-a)(p-b)(p-c)

Trong bại p=½ (a+b+c)

2.2. Công thức tính diện tích S tam giác lúc biết góc

Nếu vô tình huống chúng ta hiểu rằng số đo 2 cạnh và số đo của góc được tạo nên vày 2 cạnh thì nhằm tính diện tích S tam giác  chúng ta cũng có thể vận dụng công thức sau:

S = một nửa a.b.sinC = một nửa a.c.sinB = một nửa b.c.sinA

Trong đó:

• S: là diện tích S tam giác
• a, b, c: là chừng lâu năm những cạnh
• A, B, C: là số đo những góc

2.3. Công thức tính diện tích S tam giác vuông

Tam giác vuông là tình huống tam giác với 2 cạnh vuông góc cùng nhau và tạo nên trở nên một góc 90 chừng. 

Nếu mong muốn tính diện tích S tam giác vuông những chúng ta cũng có thể vận dụng những công thức tính thường thì. Trong khi, những chúng ta cũng có thể vận dụng công thức sau:

Xem thêm: Danh Từ Trong Tiếng Anh (2024 mới) - EnglishCentral Blog

S = một nửa a.b

Trong đó:

S: là diện tích S tam giác vuông

a, b: là chừng lâu năm 2 cạnh góc vuông.

» Xem thêm: Cách tính diện tích S hình tam giác vuông chuẩn chỉnh, dễ nắm bắt nhất

2.4. Công thức tính diện tích S tam giác cân

Mặc mặc dù tam giác cân nặng cũng chính là tình huống quan trọng của tam giác Lúc với 2 cạnh đều bằng nhau, tuy nhiên lại không tồn tại công thức riêng rẽ này nhằm dùng tính diện tích S của loại tam giác này. Do bại, chúng ta cũng có thể vận dụng ngẫu nhiên công thức tính diện tích S tam giác này nhằm tính diện tích S tam giác cân nặng. Ví dụ:

S = 1/2 a.h

Trong đó:

• S: là diện tích S tam giác cân
• a: là chừng lâu năm cạnh đáy
• h: là độ cao hạ kể từ đỉnh xuống cạnh đáy

» Xem thêm: Tam giác cân nặng là gì? Cách tính diện tích S tam giác cân

2.5. Công thức tính diện tích S tam giác vuông cân

Do tam giác vuông cân nặng với cạnh lòng vày độ cao nên những lúc tính diện tích S vuông cân nặng hoàn toàn có thể vận dụng công thức sau:

S = một nửa a²

Trong đó:

• S: là diện tích S tam giác vuông cân
• a: là chừng lâu năm cạnh đáy

» Xem thêm: Các công thức diện tích S tam giác vuông cân

2.6. Công thức tính diện tích S tam giác đều

Tam giác đều là tình huống tam giác với 3 cạnh và 3 góc đều bằng nhau. Tính diện tích S tam giác đều cũng hoàn toàn có thể vận dụng những công thức cộng đồng tính diện tích S tam giác. Tuy nhiên, 3 cạnh của tam giác đều đều bằng nhau nên chúng ta cũng có thể vận dụng công thức sau:

S = 3/4 a² 

Xem thêm: Mất điện tiếng anh là gì

Trong đó:

• S: là diện tích S tam giác
• a: cạnh của tam giác

» Xem thêm: Công thức tính diện tích S tam giác đều cạnh a không hề thiếu, chi tiết

Hy vọng với toàn bộ những công thức tính diện tích S tam giác tuy nhiên VOH Giáo dục đào tạo vừa vặn cung ứng hoàn toàn có thể chung những em học viên dễ dàng và đơn giản vận dụng trong công việc giải những Việc hình học tập. Nếu với ngẫu nhiên do dự hoặc vướng mắc này rất cần được trả lời hãy tương tác với công ty chúng tôi sẽ được tương hỗ nhé. Chúc những em học hành tốt!