Chúng ta đã được tìm hiểu về đường trung tuyến của một tam giác. Vậy đường trung tuyến trong tam giác đều có những tính chất gì khác so với các tam giác khác. Cùng tìm hiểu qua bài viết dưới đây.
1. Nhắc lại về đường trung tuyến trong một tam giác
- Đường trung tuyến trong tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm cạnh đối diện
- Một số tính chất:
+ Mỗi tam giác có ba đường trung tuyến được kẻ từ ba đỉnh của tam giác
+ Ba đường trung tuyến này cắt nhau tại một điểm và điểm đó được gọi là trọng tâm của tam giác.
2. Các tính chất đường trung tuyến trong tam giác đều
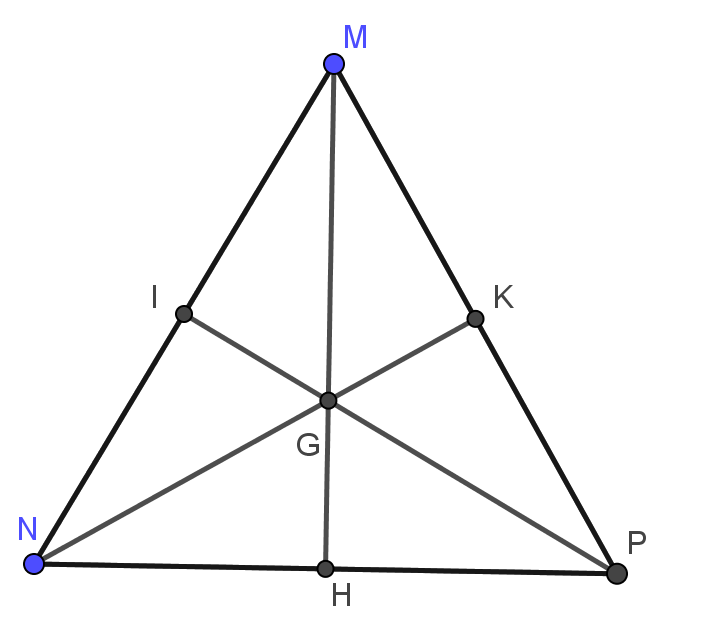
- Ba đường trung tuyến trong tam giác đều có độ dài bằng nhau.
Ví dụ: Trong tam giác MNP có ba đường trung tuyến MH, PI, NK thì
MH = PI = NK
- Các đường trung tuyến trong tam giác đều đồng thời sẽ là đường cao, đường phân giác, đường trung trực
Các đường trung tuyến MH, PI, NK đồng thời cũng là
+ Các đường cao MH, PI, NK
+ Các đường phân giác MH, PI, NK
+ Các đường trung trực MH, PI, NK
- Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng
Với G là trọng tâm thì MG =
- Khoảng cách từ trọng tâm đến trung điểm mỗi cạnh bằng
GH =
- Mỗi đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau
- Ba đường trung tuyến của tam giác đều chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau
3. Bài tập về đường trung tuyến trong tam giác đều
3.1. Dạng 1: Một số câu hỏi củng cố lý thuyết
*Phương pháp giải: Dựa vào phần lý thuyết đã nêu trên để chọn đáp án đúng
Câu 1: Cho tam MNP đều, trung tuyến MH, G là trọng tâm thì:
A. MH = 3MG
B. 2MH = 3MG
C. GH =
D. MH =
ĐÁP ÁN
Dựa vào tính chất đường trung tuyến của tam giác ta chọn đáp án đúng là B
Câu 2: Giao điểm của ba đường trung tuyến trong tam giác được gọi là:
A. Trực tâm
B. Tâm đường tròn nội tiếp tám giác
C. Tâm đường tròn ngoại tiếp tam giác
D. Trọng tâm
ĐÁP ÁN
Ba đường trung tuyến này cắt nhau tại một điểm và điểm đó được gọi là trọng tâm của tam giác.
⇒ Chọn đáp án D
Câu 3: Tam giác MNP có hai đường trung tuyến MH = NK thì:
A. MNP là tam giác đều
B. MNP là tam giác cân
C. MNP là tam giác vuông cân
D. MNP là tam giác vuông
ĐÁP ÁN
Dựa vào tính chất đường trung tuyến trong tam giác đều ta chọn đáp án A
3.2. Dạng 2: Tìm mối liên hệ giữa các đoạn thẳng trong tam giác
*Phương pháp giải: Dựa vào các tính chất của đường trung tuyến của tam giác đều để tìm được mối liên hệ giữa các đoạn thẳng trong tam giác đó
Bài tập luyện tập
Cho tam giác MNP cân tại M và MN = NP. Cho MH là trung tuyến kẻ từ đỉnh M, PI là trung tuyến kẻ từ đỉnh P, NK là trung tuyến kẻ từ đỉnh N. Gọi G là trọng tâm của tam giác MNP. Tìm mối liên hệ giữa các đoạn thẳng
a) NG và MH
b) NK và GH
c) GI và MG
ĐÁP ÁN

Ta có: MNP cân tại M ⇒ MN = MP
Mà MN = NP
⇒ MN = MP = NP ⇒ Tam giác MNP là tam giác đều
a) NG và MH
Vì NK, MH là các tiếp tuyến của tam giác MNP nên NK = MH
Mà NG =
⇒ NG =
b) NK và GH
Vì NK, MH là các tiếp tuyến của tam giác MNP nên NK = MH
Mà MH = 3GH (theo tính chất của đường trung tuyến trong tam giác)
⇒ NK = 3GH
c) GI và MG
Vì PI, MH là các tiếp tuyến của tam giác MNP nên PI = MH
Có: GI =
MG =
⇒ GI =
3.3. Dạng 3: Dạng bài tập tính toán và chứng minh liên quan đến đường trung tuyến
*Phương pháp giải: Dựa vào khái niệm và các tính chất của đường trung tuyến trong tam giác đều, yêu cầu của bài toán để giải bài toán
Bài tập luyện tập
Bài 1: Cho tam giác MNP đều có trung tuyến NK, MH. Biết NK = 9. G là trọng tâm. Tính độ dài
a) Đoạn thẳng MH
b) Đoạn thằng NG, GH
c) Đoạn thẳng MH
ĐÁP ÁN
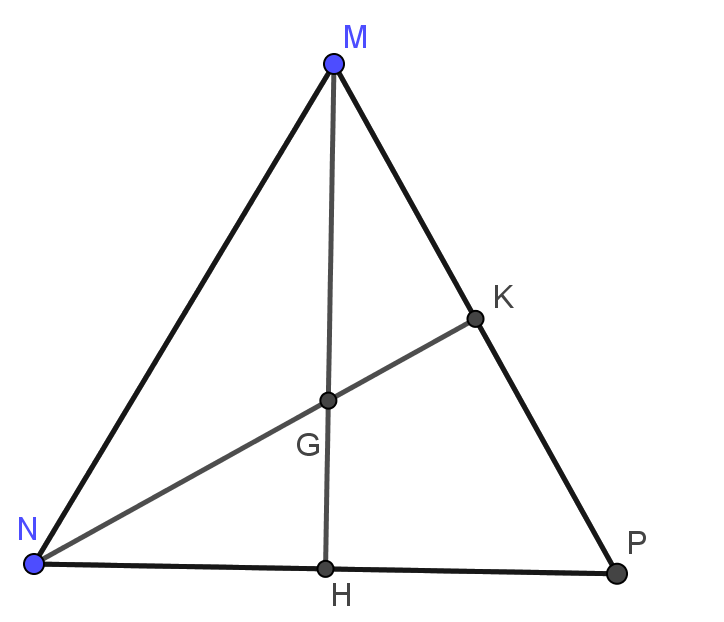
a) Đoạn thẳng MH
Tam giác MNP đều ⇒ MH = NK (tính chất)
Mà NK = 9 ⇒ MH = 9
Vậy MH = 9
b) Đoạn thằng NG, GH
Theo tính chất đường trung tuyến trong tam giác, có:
NG =
GH =
Vậy NG = 6, GH = 3.
Bài 2: Cho tam giác MNP là tam giác đều, có các trung tuyến MH, PI. MH cắt PI tại G. Biết MG = 12.
a) Chứng minh rằng NG vuông góc với MP
b) Tính độ dài các đoạn thẳng MH, PI, NG
ĐÁP ÁN
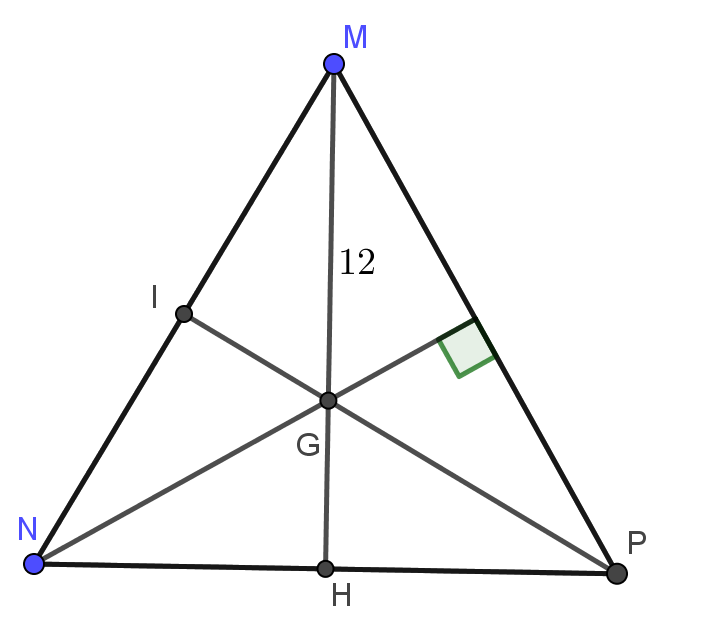
a) Chứng minh rằng NG vuông góc với MP
Ta có: Hai đường trung tuyến MH, PI cắt nhau tại G ⇒ G là trọng tâm của tam giác
⇒ NG là trung tuyến của tam giác
Tam giác MNP đều ⇒ NG vừa là trung tuyến vừa là đường cao ⇒ NG vuông góc với MP
b) Tính MH, PI, GI
MH =
PI = MH (tính chất đường trung tuyến trong tam giác đều)
⇒ PI = 18
Có: GI =
Vậy MH = 18; PI = 18; GI = 6.
Bài viết trên đây là toàn bộ các tính chất đường trung tuyến trong tam giác đều, cách tính đường trung tuyến trong tam giác đều và một số dạng bài tập phổ biến. Hy vọng bài viết này sẽ giúp các bạn học sinh hiểu rõ hơn về chủ đề này và vận dụng để làm các bài tập liên quan.
Chịu trách nhiệm nội dung: GV NGuyễn Thị Trang










