Hướng dẫn 4 cách xét dấu của tam thức bậc hai (có ví dụ)

Xin xin chào toàn bộ chúng ta, thời điểm hôm nay tất cả chúng ta tiếp tục cùng với nhau tìm hiểu hiểu về cách xét lốt tam thức bậc hai.

Tương tự động như việc xét lốt nhị thức, việc xét lốt tam thức bậc nhì là sự việc thực hiện cực kỳ thông thường gặp gỡ khi giải toán, nhất là khi giải những dạng toán như phương trình chứa chấp lốt độ quý hiếm vô cùng, bất phương trình, hệ bất phương trình, …

Bạn đang xem: Hướng dẫn 4 cách xét dấu của tam thức bậc hai (có ví dụ)

Và ở vô nội dung bài viết này bản thân tiếp tục trình diễn với chúng ta 4 cơ hội không giống nhau nhằm tiến hành xét lốt tam thức bậc 2, tùy nằm trong vô thói quen thuộc, câu hỏi ví dụ nhưng mà chúng ta hãy Để ý đến lựa lựa chọn sao mang đến thích hợp nhé.

I. Tam thức bậc nhì là biểu thức như vậy nào?

Tam thức bậc nhì so với x là biểu thức sở hữu dạng $f(x)=ax^2+bx+c$ với $a \in R^*, b \in R, c \in R$

Một cơ hội nôm mãng cầu tớ hoàn toàn có thể hiểu tam thức bậc nhì là nhiều thức sở hữu thân phụ số hạng.

Ví dụ: $f(x)=x^2-3x+2, g(x)=x^2-2x+1, h(x)=x^2+2x+3$ là những tam thức bậc nhì.

II. Cách xét lốt của tam thức bậc hai

Okay, giờ đây tất cả chúng ta tiếp tục trải qua từng mục nhé, cũng khá giản dị thôi chúng ta ạ !

#1. Bảng xét lốt tam thức

Trường hợp ý 1. $\Delta<0$ ko nhất thiết phải tạo bảng xét lốt.

Trường hợp ý 2. $\Delta=0$ và $-\frac{b}{2a}$ là nghiệm kép của tam thức $f(x)=ax^2+bx+c$

Trường hợp ý 3. $\Delta>0$ và $x_1, x_2$ là nhì nghiệm phân biệt của tam thức bậc nhì $f(x)=ax^2+bx+c$

Giả sử $x_1<x_2$

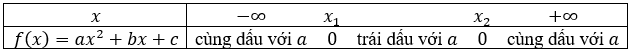
#2. Các bước xét lốt tam thức bậc 2

• Bước 1. Tìm nghiệm của tam thức $f(x)=ax^2+bx+c$, nôm mãng cầu là giải phương trình $f(x)=0$
• Bước 2. Lập bảng xét lốt tương tự động Trường hợp ý 2 hoặc Trường hợp ý 3
• Bước 3. Tiến hành xét lốt vị 1 trong các tư cơ hội mặt mũi dưới

#3. Bốn cơ hội xét lốt của tam thức bậc nhì thông thường sử dụng nhất

Cách #1. Sử dụng ấn định lý

Cho $f(x)=ax^2+bx+c$ $(a \neq 0), \Delta=b^2-4ac$

• Nếu $\Delta<0$ thì $f(x)$ luôn luôn nằm trong lốt với thông số $a$, với từng $x \in R$
• Nếu $\Delta=0$ thì $f(x)$ luôn luôn nằm trong lốt với thông số $a$, nước ngoài trừ $x=-\frac{b}{2a}$
• Nếu $\Delta>0$ thì $f(x)$ nằm trong lốt với thông số $a$ khi $x<x_1$ hoặc $x>x_{2}$, trái ngược lốt với thông số $a$ khi $x_1<x<x_2$ vô cơ $x_1, x_2$ $(x_1<x_2)$ là nhì nghiệm của $f(x)$

Cách #2. Sử dụng mẹo

Chúng tớ tiếp tục dùng mẹo ghi nhớ “khoảng ở đầu cuối lốt với thông số $a$ qua loa nghiệm đơn thay đổi lốt, qua loa nghiệm kép không thay đổi dấu”

Đây là mẹo ghi nhớ của tôi, tùy vô cơ hội suy nghĩ và thói quen thuộc nhưng mà sẽ có được những mẹo ghi nhớ không giống. Tuy nhiên, toàn bộ đều sở hữu cộng đồng một chân thành và ý nghĩa và đều được suy đi ra kể từ ấn định lý bên trên.

Cách #3. Sử dụng độ quý hiếm đại diện

Giả sử tam thức $f(x)=ax^2+bx+c$ sở hữu nhì nghiệm phân biết là $x_1, x_2$ và $x_1<x_2$

• Lấy một độ quý hiếm $x_0$ bất kì nằm trong khoảng tầm $(-\infty, x_1)$
• Tính độ quý hiếm $f(x_0)=ax_0^2+bx_0+c$
• Nếu $f(x_0) > 0$ thì $+$ ngược lại thì $–$

Thực hiện nay tương tự động nhằm xét lốt f(x) khi x nằm trong khoảng tầm $(x_1, x_2); (x_2, +\infty)$

Cách #4. Quy về sự xét lốt nhị thức bậc nhất

Mình ko khuyến nghị chúng ta dùng sử dụng phương pháp này và sử dụng phương pháp này cũng chỉ dùng được khi tam thức sở hữu nghiệm

Phân tích tam thức $f(x)=ax^2+bx+c$ kết quả của nhì nhị thức $f(x)=a(x-x_1)(x-x_2)$ với $x_1, x_2$ là nghiệm của tam thức bậc hai  $f(x)=ax^2+bx+c$

Xét vết tích của nhì nhị thức rồi suy đi ra lốt của tam thức

#4. Ví dụ minh họa về kiểu cách xét lốt của tam thức bậc 2

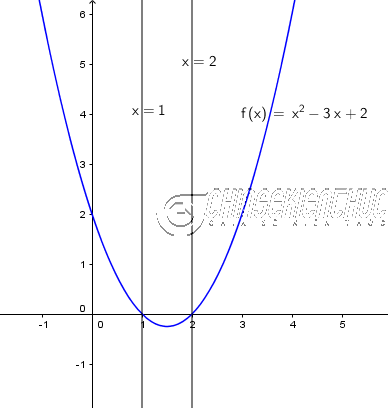
Ví dụ 1. Xét lốt tam thức $f(x)=x^2-3x+2$

Lời giải:

$f(x)=x^2-3x+2$ sở hữu nhì nghiệm phân biệt $x_1=1, x_2=2$ và thông số $a=1>0$

Ta sở hữu bảng xét dấu:

Vậy:

• $f(x)>0$ khi $x \in (-\infty, 1) \cup (2, +\infty)$
• $f(x)<0$ khi $x \in (1,2)$
• $f(x)=0$ khi $x=1$ hoặc $x=2$

Xem thêm: 7 hình nền đẹp bầu trời gợi cảm hứng cho những ngày mưa gió

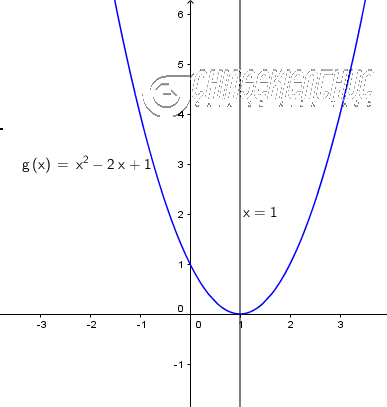
Ví dụ 2. Xét lốt tam thức $g(x)=x^2-2x+1$

Lời giải:

$g(x)=x^2-2x+1$ sở hữu một nghiệm kép có một không hai $x=1$ và thông số $a=1>0$

Ta sở hữu bảng xét dấu:

Vậy:

• $g(x)>0$ khi $x \in (-\infty, 1) \cup (1, +\infty)$
• $g(x)=0$ khi $x=1$

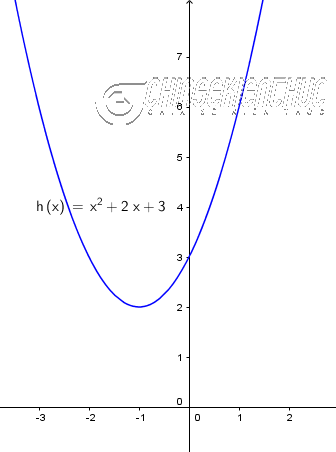
Ví dụ 3. Xét lốt tam thức $h(x)=x^2+2x+3$

Lời giải:

Cách 1. $h(x)$ sở hữu $\Delta=-8<0$ và thông số $a=1>0$ nên $h(x)>0$ với từng $x \in (-\infty, +\infty)$

Cách 2. $h(x)=x^2+2x+3=(x+1)^2+2>0$ với từng $x \in (-\infty, +\infty)$

III. Xét vết tích, thương những tam thức bậc hai

Tương tự động tích, thương của những nhị thức hàng đầu, tớ cũng hoàn toàn có thể xét vết tích, thương của những tam thức bậc nhì một cơ hội khá là giản dị.

Ví dụ 5. Xét lốt $f(x)=\frac{(x^2-3x+2)(x^2-2x+1)}{x^2+2x+3}$

Lời giải:

Vì $x^2+2x+3=(x+1)^2>0$ từng $x \in (-\infty, +\infty)$ nên f(x) xác lập với từng $x \in (-\infty, +\infty)$

Các tam thức $x^2-3x+2, x^2-2x+1$ sở hữu những nghiệm theo thứ tự là $1, 2, 1$ (nghiệm kép)

Các nghiệm được ghi chép theo đòi trật tự tăng dần dần là $1, 2$

Các nghiệm này phân chia khoảng tầm $(-\infty, +\infty)$ trở nên thân phụ khoảng tầm là $(-\infty, 1); (1,2); (2, +\infty)$

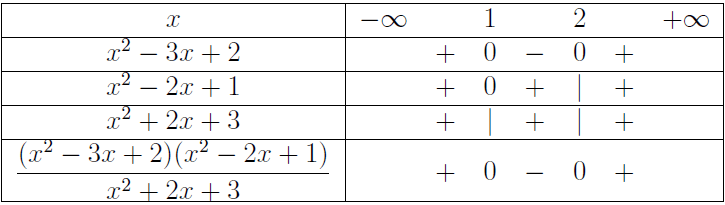
Vậy …

• $f(x)>0$ khi $x \in (-\infty, 1) \cup (2, +\infty)$
• $f(x)<0$ khi $x \in (1, 2)$
• $f(x)=0$ khi $x=1$ hoặc $x=2$

IV. Lời kết

Về cơ phiên bản sở hữu tư cách nhằm xét lốt tam thức bậc hai, cá thể bản thân nhận định rằng Cách 2 và Cách 3 là tối ưu nhất với đa số những tình huống.

Thật vậy, …

• Cách 1. Khó nhớ
• Cách 2. Dễ nhớ
• Cách 3. Dễ ghi nhớ và vận dụng được với nhị thức, tam thức và nhiều thức sở hữu bậc bất kì
• Cách 4. Tốn nhiều thời gian

Hi vọng là qua loa nội dung bài viết này thì chúng ta vẫn hiểu rộng lớn về dấu của tam thức bậc hai. Xin Chào thân ái và hứa hẹn hội ngộ chúng ta trong mỗi nội dung bài viết tiếp theo sau !

Đọc thêm:

Xem thêm: Từ vựng 15 loại ghế trong tiếng Anh

• 7 cơ hội giải phương trình bậc hai đơn giản, hiệu quả
• Cách vẽ đồ vật thị hàm số bậc hai (trên giấy tờ và bên trên máy tính)
• GeoGebra: Hỗ trợ dạy dỗ học tập ấn định lý về lốt của tam thức bậc hai

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com