%C4%90%C3%B4ng%20Nam%20%C3%81 trong Tiếng Anh, dịch
"%C4%90%C3%B4ng%20Nam%20%C3%81" như thế nào trong Tiếng Anh? Kiểm tra bản dịch của "%C4%90%C3%B4ng%20Nam%20%C3%81" trong từ điển Tiếng Việt - Tiếng Anh Glosbe
Giải bài bác 4: Thể tích của hình lăng trụ đứng - Sách VNEN toán 8 luyện 2 trang 99. Phần bên dưới tiếp tục chỉ dẫn vấn đáp và trả lời những thắc mắc vô bài học kinh nghiệm. Cách thực hiện cụ thể, dễ nắm bắt, Hi vọng những em học viên tóm đảm bảo chất lượng kỹ năng và kiến thức bài học kinh nghiệm.
A. HOẠT ĐỘNG KHỞI ĐỘNG
Quan sát hình 92, hiểu và nhận xét
Bạn đang xem: Giải toán VNEN 8 bài 4: Thể tích của hình lăng trụ đứng
Em hãy cho thấy thể tích của hình vỏ hộp chữ nhật sở hữu vì chưng diện tích S lòng nhân với độ cao không?
Trả lời:
Gọi phỏng nhiều năm độ cao của hình vỏ hộp chữ nhật là a, phỏng nhiều năm nhị lòng là b,c
Diện tích lòng là S = b.c
Công thức tính thể tích của hình vỏ hộp chữ nhật là V = a.b.c = a.(b.c) = a.S
Vậy thể tích của hình vỏ hộp chữ nhật vì chưng diện tích S lòng nhân với độ cao.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. a) Quan sát hình và nêu nhận xét
* Em hãy cho thấy thể tích của hình lăng trụ đứng sở hữu lòng là hình chữ nhật (h.93).
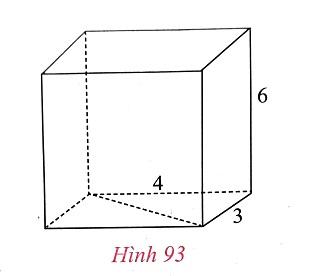
Trả lời:
Thể tích của hình lăng trụ đứng sở hữu lòng là hình chữ nhật là: V = 6.3.4 = 72
* Em hãy đối chiếu thể tích của hình lăng trụ đứng sở hữu lòng là tam giác vuông (h.94) với thể tích của hình lăng trụ đứng sở hữu lòng là hình chữ nhật (h.93).
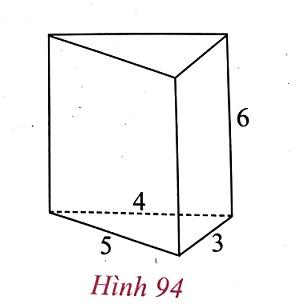
Trả lời:
Thể tích của hình lăng trụ đứng sở hữu lòng là hình tam giác vuông là: V' = 6.$\frac{1}{2}$.3.4 = 36
Ta có: $\frac{V'}{V}$ = $\frac{36}{72}$ = $\frac{1}{2}$
Vậy thể tích của hình lăng trụ đứng sở hữu lòng là tam giác vuông (h.94) bằng $\frac{1}{2}$ thể tích của hình lăng trụ đứng sở hữu lòng là hình chữ nhật (h.93).
B. Bài luyện và chỉ dẫn giải
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 100 sách VNEN 8 luyện 2
Cho hình lăng trụ đứng ABC.A'B'C' sở hữu tam giác ABC là tam giác vuông bên trên A. Em hãy điền vô địa điểm (...) mang đến đúng:
AB | AC | Diện tích của một đáy | AA’ | Thể tích của hình lăng trụ |
2cm | 3cm | 4cm | ||
9cm | 18$cm^{2}$ | 5cm | ||
3cm | 4cm | 48$cm^{3}$ |
Câu 2: Trang 100 sách VNEN 8 luyện 2
Cho hình lăng trụ đứng ABCD.A'B'C'D' sở hữu tam giác ABCD là hình chữ nhật. Em hãy điền vô địa điểm (...) mang đến đúng:
AB | AD | Diện tích của một đáy | AA’ | Thể tích của hình lăng trụ |
3cm | 5cm | 8cm | ||
4cm | 20$cm^{2}$ | 3cm | ||
2cm | 7cm | 56$cm^{3}$ |
Câu 3: Trang 100 sách VNEN 8 luyện 2
Cho hình lăng trụ đứng ABCD.A'B'C'D' sở hữu AA' = 3cm, ABCD là hình thang với nhị lòng AB và CD theo lần lượt là 4cm và 6cm, đàng cao của hình thang là 5cm. Tính thể tích của hình lăng trụ đứng.
Câu 4: Trang 100 sách VNEN 8 luyện 2
Cho hình lăng trụ đứng ABC.A'B'C' sở hữu ABC là tam giác vuông bên trên A. Tính thể tích của hình lăng trụ biết AA' = 8cm, AB = 3cm, BC = 5cm.
Câu 5: Trang 100 sách VNEN 8 luyện 2
Cho hình lăng trụ đứng ABCD.A'B'C'D' sở hữu ABCD là hình chữ nhật. Tính thể tích của hình lăng trụ biết AA' = 8cm, AB = 5cm, AC = 13cm.
D. HOẠT ĐỘNG VẬN DỤNG
Câu 1: Trang 100 sách VNEN 8 luyện 2
Một lăng kính sở hữu hình trạng lăng trụ đứng với lòng là tam giác vuông như hình 95. Tính thể tích của lăng kính.
Câu 2: Trang 101 sách VNEN 8 luyện 2
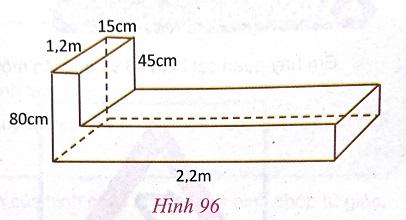
Một loại chóng được sản xuất được làm bằng gỗ sở hữu hình trạng chữ L như hình 96. Tính thể tích của loại chóng.
Câu 3: Trang 101 sách VNEN 8 luyện 2
Một loại lưỡi rìu bao gồm nhị phần. Phần loại nhất sở hữu hình trạng vỏ hộp chữ nhật với những độ cao thấp là 2cm, 4cm, 6cm. Phần loại nhị sở hữu dạng một hình lăng trụ tam giác với lòng là tam giác cân nặng sở hữu cạnh lòng băng 2cm và đàng cao ứng vì chưng 5cm, đàng cao của hình lăng trụ tam giác vì chưng 4cm. Tính thể tích của lưỡi rìu (h.97).
E. HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG
Cho hình lăng trụ đứng ABCDE.A'B'C'D'E' sở hữu lòng là ngũ giác. lõi AA' = 4cm, tứ giác ABCE là hình vuông vắn cạnh 6cm, tam giác CDE vuông cân nặng bên trên D. Tính thể tích của hình lăng trụ đứng ABCDE.A'B'C'D'E'.
Từ khóa lần kiếm: giải bài bác 4 thể tích của hình lăng trụ đứng, thể tích của hình lăng trụ đứng trang 99 vnen toán 8, bài bác 4 sách vnen toán 8 luyện 2, giải sách vnen toán 8 luyện 2 cụ thể dễ nắm bắt