Chủ đề thể tích khối lăng trụ lớp 12: Khám phá bí mật về "Thể Tích Khối Lăng Trụ Lớp 12" qua bài viết chi tiết này! Từ định nghĩa cơ bản đến công thức tính toán chính xác, cùng với các ví dụ minh họa và bài tập áp dụng, chúng tôi sẽ giúp bạn nắm vững kiến thức và áp dụng thành thạo. Hãy cùng chúng tôi khám phá cách dễ dàng đạt điểm cao trong kỳ thi, mở rộng kiến thức về thể tích khối lăng trụ, một trong những dạng toán quan trọng của lớp 12.
Tính Thể Tích Khối Lăng Trụ Lớp 12
1. Định nghĩa và Công thức tính thể tích
Hình lăng trụ được định nghĩa là một đa giác có hai mặt đáy song song và bằng nhau, với mặt bên là hình bình hành. Thể tích khối lăng trụ được tính bằng công thức V = B.h, trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
2. Các loại lăng trụ thường gặp
- Lăng trụ đứng: Các cạnh bên vuông góc với đáy và các mặt bên là hình chữ nhật.
- Lăng trụ đều: Là lăng trụ đứng có đáy là đa giác đều.
- Hình hộp: Lăng trụ có đáy là hình bình hành.
3. Ví dụ minh họa
- Đối với lăng trụ hình chữ nhật, sử dụng công thức V = S.h, trong đó S là diện tích đáy và h là chiều cao.
- Đối với lăng trụ hình tam giác, cũng sử dụng công thức V = S.h.
- Đối với lăng trụ hình tròn, sử dụng công thức V = π.r^2.h, với r là bán kính đáy.
Để tính diện tích đáy, ta cần áp dụng công thức tương ứng với từng hình đáy. Ví dụ, diện tích đáy của hình vuông là S = a^2, với a là độ dài cạnh của hình vuông.
| Hình dạng đáy | Công thức diện tích đáy (S) |
| Hình vuông | S = a^2 |
| Hình chữ nhật | S = a * b |
| Hình tam giác đều | S = (sqrt(3) * a^2) / 4 |
| Hình tròn | S = π * r^2 |
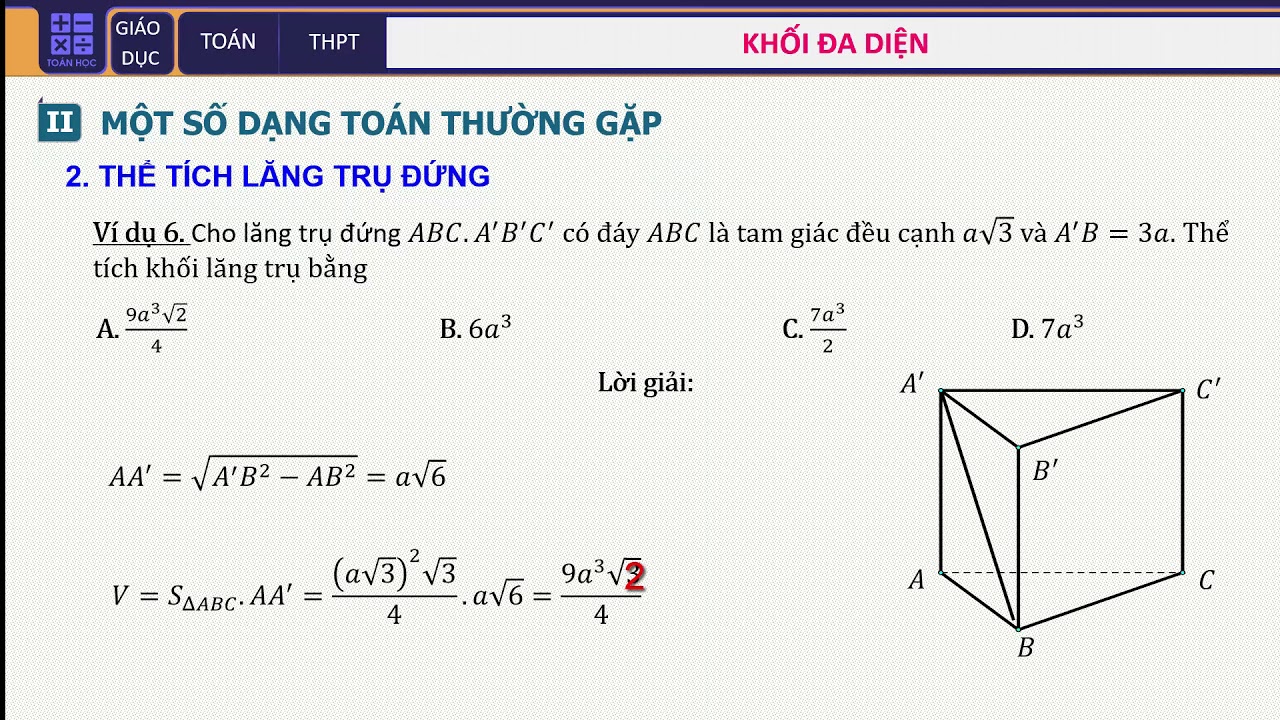
Làm sao để tính thể tích khối lăng trụ trong chương trình học của lớp 12?
Để tính thể tích của khối lăng trụ trong chương trình học của lớp 12, chúng ta có thể sử dụng công thức:
- Xác định diện tích đáy (S) và chiều cao (h) của khối lăng trụ.
- Sử dụng công thức: Thể tích (V) = diện tích đáy (S) * chiều cao (h).
Thể Tích Khối Lăng Trụ Toán 12 Full Dạng Phần 1 Thầy Nguyễn Phan Tiến
Từ khóa \"Thể tích khối lăng trụ\" và \"Tỉ lệ\" chứa kiến thức hấp dẫn. Hãy đắm chìm vào video để khám phá những điều mới lạ và thú vị trong học tập!
Tỉ Lệ Thể Tích Khối Lăng Trụ Toán 12 Thầy Nguyễn Phan Tiến
Tỉ Lệ Thể Tích Khối Lăng Trụ (Toán 12) | Thầy Nguyễn Phan Tiến Đăng kí học Đầy Đủ Video Lý Thuyết và Bài Tập Tự Luyện ...
1. Định nghĩa khối lăng trụ
Khối lăng trụ được định nghĩa thông qua việc xét hai mặt phẳng song song, trên mặt phẳng này vẽ một đa giác lồi. Từ các đỉnh của đa giác này, dựng các đường thẳng song song chạm vào mặt phẳng thứ hai tạo thành đa giác thứ hai tương ứng. Hình được tạo bởi hai đa giác này và các hình bình hành nối các cạnh tương ứng giữa hai đa giác được gọi là khối lăng trụ. Các mặt bên của hình lăng trụ đều và song song với nhau, tạo thành các hình bình hành, và hai đáy của hình lăng trụ là hai đa giác bằng nhau.
Có nhiều loại lăng trụ dựa vào tính chất của đáy và mối quan hệ giữa cạnh bên và đáy như lăng trụ đứng (các cạnh bên vuông góc với đáy và mặt bên là hình chữ nhật), lăng trụ đều (lăng trụ đứng có đáy là đa giác đều), hình hộp (lăng trụ có đáy là hình bình hành) và hình lập phương (một dạng đặc biệt của hình hộp với tất cả các cạnh bằng nhau).
Việc tính thể tích khối lăng trụ dựa trên công thức V = B.h, với B là diện tích đáy và h là chiều cao của lăng trụ. Đối với từng dạng đáy cụ thể, có những công thức tính diện tích đáy tương ứng để áp dụng vào công thức tổng quát này.
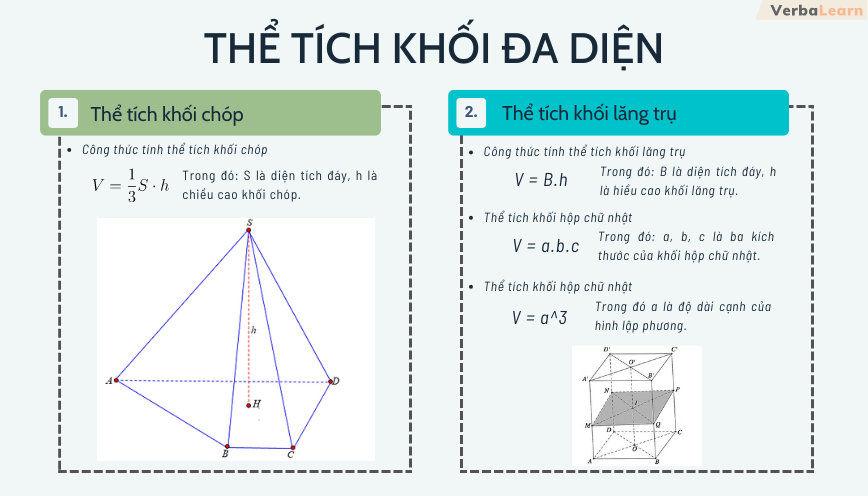
2. Công thức tính thể tích khối lăng trụ
Thể tích của khối lăng trụ được xác định qua công thức cơ bản V = S x h, trong đó V là thể tích của khối lăng trụ, S là diện tích của một mặt đáy, và h là chiều cao của khối lăng trụ. Điều này áp dụng cho mọi dạng lăng trụ, bao gồm lăng trụ đứng, lăng trụ đều, và các dạng khác như lăng trụ hình chữ nhật, lăng trụ hình tam giác, và lăng trụ hình tròn, tùy thuộc vào hình dạng cụ thể của mặt đáy.
- Lăng trụ hình chữ nhật: V = S.h, với S = a x b (a và b là chiều dài và chiều rộng của đáy).
- Lăng trụ hình tam giác: V = S.h, với S = (sqrt(3)/4) x a^2 (a là cạnh của tam giác đều).
- Lăng trụ hình tròn: V = π.r^2.h, với r là bán kính của đáy tròn.
Việc tính diện tích đáy S phụ thuộc vào hình dạng cụ thể của đáy. Ví dụ, đối với một hình vuông, S = a^2; đối với một hình chữ nhật, S = a x b; đối với một hình tam giác đều, S = (sqrt(3)/4) x a^2; và đối với một hình tròn, S = π x r^2, với a là độ dài cạnh của hình vuông hoặc hình tam giác đều, b là chiều rộng của hình chữ nhật, và r là bán kính của hình tròn.

3. Các loại lăng trụ thường gặp và cách tính thể tích
Thể tích của khối lăng trụ được tính bằng công thức V = B.h, trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
- Lăng trụ đứng
- Đặc điểm: Các cạnh bên vuông góc với mặt đáy, mặt bên là hình chữ nhật. Diện tích đáy có thể được tính dựa trên hình dạng cụ thể của đáy, như tam giác, hình vuông, hình chữ nhật.
- Lăng trụ đều
- Đặc điểm: Là lăng trụ đứng có đáy là đa giác đều. Tất cả các mặt bên đều là hình chữ nhật bằng nhau.
- Hình hộp và hình lập phương
- Hình hộp chữ nhật
- Thể tích: V = l.w.h, với l là chiều dài, w là chiều rộng, và h là chiều cao.
- Hình lập phương
- Thể tích: V = a3, với a là độ dài cạnh của hình lập phương.
3.1 Lăng trụ đứng
Lăng trụ đứng được định nghĩa là lăng trụ có các cạnh bên vuông góc với mặt đáy, khiến cho các mặt bên của nó trở thành hình chữ nhật. Điều này cũng đồng nghĩa với việc chiều cao của lăng trụ chính là độ dài của các cạnh bên.
Các tính chất của lăng trụ đứng bao gồm:
- Các cạnh bên song song và bằng nhau.
- Các mặt bên là hình bình hành, cụ thể là hình chữ nhật trong trường hợp này.
- Hai đáy của lăng trụ là hai đa giác bằng nhau và nằm trong hai mặt phẳng song song.
Để tính thể tích của lăng trụ đứng, ta sử dụng công thức V = B.h, trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
Ví dụ, đối với một lăng trụ đứng có đáy là tam giác vuông cân tại B với AC = a√2 và BC\" = 2a, thể tích của khối lăng trụ ABC.A’B’C’ có thể được tính toán dựa trên diện tích đáy và chiều cao của lăng trụ.

3.2 Lăng trụ đều
Lăng trụ đều là loại lăng trụ đặc biệt với đáy là đa giác đều và các cạnh bên vuông góc với mặt đáy, khiến cho các mặt bên của nó là các hình chữ nhật bằng nhau. Điều này tạo nên tính đối xứng và cân đối cho lăng trụ đều, giúp việc tính toán thể tích trở nên đơn giản và chính xác hơn.
- Tính chất:
- Các mặt bên là hình chữ nhật bằng nhau.
- Cạnh bên chính là chiều cao của lăng trụ, đồng thời cũng là đường cao trong các hình chữ nhật của mặt bên.
- Hai mặt đáy là hai đa giác đều và song song với nhau.
- Công thức tính thể tích:
- V = B.h, trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
Ví dụ về lăng trụ đều có thể kể đến là khối lăng trụ tam giác đều, tứ giác đều, nơi mà đáy là đa giác đều và các cạnh bên tạo với đáy một góc vuông. Cách tính thể tích của những khối này được thực hiện qua việc xác định diện tích đáy và chiều cao của lăng trụ.
3.3 Hình hộp và hình lập phương
Hình hộp và hình lập phương là hai dạng cơ bản của khối lăng trụ, mỗi loại có đặc điểm và công thức tính thể tích riêng biệt.
- Hình hộp
- Hình hộp, hay hình hộp chữ nhật, là khối lăng trụ có đáy là hình bình hành. Đặc biệt, khi đáy là hình chữ nhật, khối lăng trụ được gọi là hình hộp chữ nhật.
- Công thức tính thể tích: V = a.b.h, với a, b là chiều dài và chiều rộng của đáy, và h là chiều cao của hình hộp.
- Hình lập phương
- Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật khi tất cả các cạnh đều bằng nhau.
- Công thức tính thể tích: V = a3, với a là độ dài cạnh của hình lập phương.
Thông qua việc hiểu rõ về hình hộp và hình lập phương, học sinh có thể áp dụng linh hoạt các công thức để giải quyết các bài toán thực tế liên quan đến thể tích trong chương trình Toán lớp 12.

4. Cách tính diện tích đáy cho các hình đáy khác nhau
Tính diện tích đáy là bước quan trọng để xác định thể tích của khối lăng trụ. Dưới đây là cách tính diện tích cho một số hình đáy thường gặp:
- Hình vuông
- Diện tích đáy (S) = cạnh2 (a2).
- Hình chữ nhật
- Diện tích đáy (S) = chiều dài × chiều rộng (l × w).
- Hình tam giác
- Diện tích đáy (S) = 1/2 × cơ sở × chiều cao (1/2 × b × h).
- Hình thoi
- Diện tích đáy (S) = 1/2 × tích của độ dài hai đường chéo (1/2 × d1 × d2).
- Hình bình hành
- Diện tích đáy (S) = cơ sở × chiều cao (b × h).
- Hình tròn
- Diện tích đáy (S) = π × bán kính2 (π × r2).
Biết cách tính diện tích đáy cho các hình khác nhau giúp học sinh dễ dàng áp dụng vào việc giải quyết các bài toán liên quan đến thể tích khối lăng trụ trong chương trình Toán lớp 12.
5. Ví dụ minh họa
- Ví dụ 1: Cho hình hộp đứng có các cạnh là AB = 3a, AD = 2a, AA’ = 2a. Bài toán yêu cầu tính thể tích của khối A’.ACD’. Cách giải: Áp dụng công thức tính thể tích khối hộp đứng.
- Ví dụ 2: Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, ∠(ACB) = 30°. Một trung điểm cạnh AC và góc giữa cạnh bên và mặt đáy của lăng trụ là 60°. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Yêu cầu tính thể tích khối lăng trụ ABC.A’B’C’.
- Ví dụ 3: Cho lăng trụ ABC.A’B’C’, đáy ABC có AC = a√3, BC = 3a, ∠(ACB) = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho HC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Yêu cầu tính thể tích khối lăng trụ ABC.A’B’C’.
Các bài toán này giúp bạn làm quen với việc áp dụng công thức thể tích khối lăng trụ trong các tình huống cụ thể, từ đó nâng cao kỹ năng giải toán và chuẩn bị tốt cho các kì thi.
6. Bài tập áp dụng
- Cho lăng trụ đứng tam giác ABC.A’B’C’ có đáy là tam giác vuông cân tại A, cạnh AB = a, góc giữa A’C và mặt phẳng (ABC) là 45°. Tính thể tích của khối lăng trụ.
- Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân, AB = AC = a, góc BAC = 120°. Mặt phẳng (AB\"C\") tạo với mặt đáy góc 60°. Tính thể tích của lăng trụ.
- Cho lăng trụ ABC.A\"B\"C\" có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A\" lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh A\"A tạo với mặt đáy góc 30°. Tính thể tích khối lăng trụ.
- Cho hình lăng trụ đứng ABC.A’B’C’ có AC = a, BC = a, góc BAC = 150°, đường thẳng B\"C tạo với mặt phẳng (ABB\"A\") một góc α thoả mãn sinα = 1/2. Tính thể tích khối lăng trụ.
- Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a, AA’ = 2a. Tính thể tích khối lăng trụ.
Các bài tập này được thiết kế để kiểm tra và cải thiện kỹ năng giải toán hình học của bạn, đặc biệt là khả năng áp dụng công thức tính thể tích khối lăng trụ vào thực tế. Hãy cố gắng làm theo từng bước và kiểm tra kỹ lưỡng các giả thiết để đạt kết quả chính xác.
Khám phá thế giới hình học với \"Thể tích khối lăng trụ lớp 12\"! Qua bài viết, bạn không chỉ hiểu rõ công thức, cách tính thể tích, mà còn được trải nghiệm qua các ví dụ minh họa sinh động và bài tập áp dụng đa dạng, giúp nắm vững kiến thức, chuẩn bị tốt nhất cho kì thi sắp tới.