Cách tính công thức tính thể tích tam giác đơn giản và hiệu quả

Tam giác là một trong những hình học tập bao gồm thân phụ đỉnh được nối cùng nhau vì thế những cạnh. Để khái niệm một cơ hội đúng mực, tam giác là một trong những phần của mặt mày phẳng lặng được xung quanh vì thế thân phụ đoạn trực tiếp được tiếp liền nhau. Mỗi đoạn trực tiếp được gọi là một trong những cạnh của tam giác và nhì đoạn trực tiếp ngẫu nhiên được nối trở nên với thân phụ đỉnh của tam giác tạo ra trở nên một góc. Khi thân phụ cạnh của tam giác đều sở hữu chừng lâu năm cân nhau, tao gọi tam giác này là tam giác đều.

Bạn đang xem: Cách tính công thức tính thể tích tam giác đơn giản và hiệu quả

Chúng tao cần thiết tính thể tích tam giác nhằm xác lập khối lăng trụ tam giác, một đối tượng người tiêu dùng hình học tập cần thiết và được dùng rộng thoải mái trong số phần mềm thực tiễn và vô toán học tập. Việc đo lường và tính toán thể tích của khối lăng trụ tam giác nhập vai trò cần thiết trong những công việc đo lường và tính toán diện tích S của mặt phẳng và lượng của những vật thể, là hạ tầng nhằm tiến hành nhiều việc làm thi công, phong cách xây dựng và khoa học tập không giống.

Công thức tính thể tích tam giác là V = 1/3 x diện tích S lòng x độ cao.
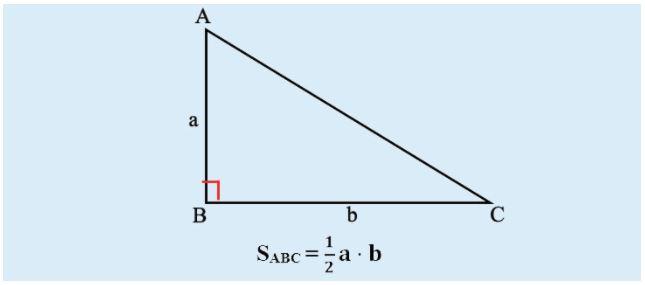
Để vận dụng công thức này, trước tiên tao cần thiết tính diện tích S lòng của tam giác vì thế công thức Diện tích = 50% x chiều lâu năm cạnh lòng x độ cao. Sau bại liệt, tao nhân sản phẩm này với độ cao và phân tách mang lại 3 nhằm tính được thể tích của tam giác.
Chú ý rằng độ cao của tam giác cần được đo vuông góc với lòng của tam giác.

Xem thêm: máy giặt tiếng anh là gì

Có thể dùng công thức tính thể tích tam giác nhằm đo lường và tính toán thể tích của một tam giác ngẫu nhiên. Công thức này được viết lách bên dưới dạng V = 1/3 x Diện tích lòng x Chiều cao. Trong số đó, Diện tích lòng là diện tích S của tam giác lòng và Chiều cao là chừng lâu năm đo kể từ đỉnh của tam giác xuống lòng theo gót đàng vuông góc. phẳng cơ hội vận dụng công thức này, tao rất có thể tính được thể tích của tam giác và vận dụng cho những Việc tương quan cho tới tam giác.

Có 3 loại tam giác chính: tam giác đều, tam giác vuông và tam giác thông thường.
1. Tam giác đều:
- Thể tích = 1/3 x diện tích S lòng x chiều cao
- Ví dụ: Một tam giác đều sở hữu lòng vì thế 6cm và độ cao vì thế 4cm. Thể tích của tam giác bại liệt là: (1/3) x (6 x 4) x 4 = 32 cm3
2. Tam giác vuông:
- Thể tích = 1/3 x diện tích S lòng x chiều cao
- Ví dụ: Một tam giác vuông sở hữu lòng vì thế 10cm, độ cao vuông góc với lòng vì thế 5cm. Thể tích của tam giác bại liệt là: (1/3) x (10 x 5) x 5 = 83,33 cm3
3. Tam giác thường:
- Thể tích = 1/3 x diện tích S lòng x chiều cao
- Ví dụ: Một tam giác thông thường sở hữu lòng vì thế 8cm, độ cao kể từ đỉnh xuống lòng vì thế 6cm. Thể tích của tam giác bại liệt là: (1/3) x (8 x 6) x 6 = 64 cm3.
Vậy này là phương pháp tính thể tích của những loại tam giác không giống nhau. Chúng tao chỉ nên biết diện tích S lòng và độ cao của tam giác nhằm rất có thể tính được thể tích của chính nó.

Xem thêm: Hình ảnh nắm tay trên xe máy đẹp, lãng mạn