con bò sữa Tiếng Anh là gì
con bò sữa kèm nghĩa tiếng anh milch cow, và phát âm, loại từ, ví dụ tiếng anh, ví dụ tiếng việt, hình ảnh minh họa và các từ liên quan
Hình thoi là 1 trong trong mỗi hình bắt gặp thật nhiều trong những vấn đề về hình học tập vô trong cả quy trình học hành của tất cả chúng ta. Cho nên những bạn phải bắt được định nghĩa, tín hiệu nhận biết và tính hóa học hình thoi thì mới có thể những thể vận dụng giải bài xích tập luyện dễ dàng và đơn giản.
Hình thoi là tứ giác sở hữu 4 cạnh mặt mày đều bằng nhau. Hình thoi là hình bình hành sở hữu nhị cạnh kề đều bằng nhau hoặc hình bình hành sở hữu hai tuyến phố chéo cánh vuông góc cùng nhau.
Bạn đang xem: định nghĩa, tính chất, dấu hiệu nhận biết hình thoi
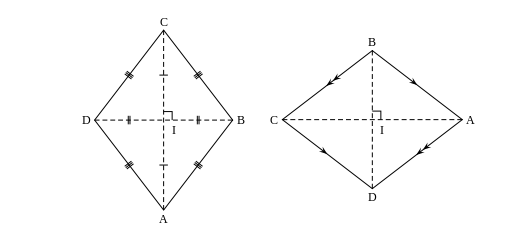
Tính hóa học hình thoi
Trong hình thoi:
- Các góc đối nhau đều bằng nhau.
- Hai lối chéo cánh vuông góc cùng nhau và rời nhau bên trên trung điểm của từng lối.
- Hai lối chéo cánh là những lối phân giác của những góc của hình thoi.
- Hình thoi sở hữu toàn bộ đặc thù của hình bình hành. Đó là: Các cạnh đối tuy vậy song và đều bằng nhau, những góc đối đều bằng nhau, hai tuyến phố chéo cánh rời nhau bên trên trung điểm từng lối.
Ngoài rời khỏi, những chúng ta cũng có thể tìm hiểu thêm thêm:
- Tính hóa học hình thang cân
- Công thức tính diện tích S hình thoi, chu vi hình thoi
Dấu hiệu phân biệt hình thoi
Hình tứ giác quánh biệt
- Tứ giác sở hữu tứ cạnh đều bằng nhau là hình thoi.
- Tứ giác sở hữu 2 lối chéo cánh là lối trung trực của nhau là hình thoi.
- Tứ giác sở hữu 2 lối chéo cánh là lối phân giác của tất cả tứ góc là hình thoi.
Hình bình hành quánh biệt
- Hình thoi là 1 trong dạng quan trọng của một hình bình hành vì như thế nó sở hữu tương đối đầy đủ đặc thù của hình bình hành và còn tồn tại một trong những đặc thù khác:
- Hình bình hành sở hữu nhị cạnh kề đều bằng nhau là hình thoi.
- Hình bình hành sở hữu hai tuyến phố chéo cánh vuông góc cùng nhau là hình thoi.
- Hình bình hành sở hữu một lối chéo cánh là lối phân giác của một góc là hình thoi.
Bài tập luyện chứng tỏ về hình thoi
Dưới đó là 4 cơ hội chứng tỏ hình thoi những chúng ta cũng có thể tham lam khảo
Cách 1: Tứ giác sở hữu tứ cạnh bởi vì nhau
Ví dụ: Cho hình chữ nhật ABCD sở hữu những trung điểm của tứ cạnh theo lần lượt là M, N, Phường, Q. Chứng minh rằng những trung điểm đó là những đỉnh của hình thoi.
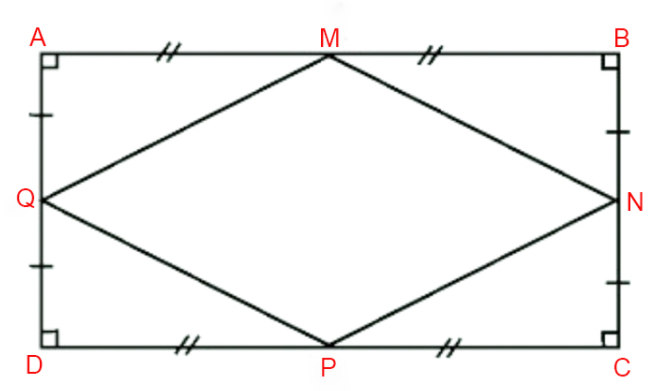
Lời giải:
Xét ΔABD sở hữu M và Q theo lần lượt là trung điểm của AB và AD.
⇒ MQ là lối khoảng của ΔABD.
⇒ MQ = ½ BD (1).
Chứng minh tương tự động tao có: MN = ½ AC; NP = ½ BD; PQ = ½ AC (2).
Vì ABCD là hình chữ nhật nên AC = BD (3).
Từ (1), (2) và (3), tao suy rời khỏi MQ = MN = NP = PQ.
⇒ Tứ giác MNPQ là hình thoi bởi sở hữu tứ cạnh đều bằng nhau.
Cách 2: Tứ giác sở hữu 2 lối chéo cánh là lối trung trực của nhau
Ví dụ: Cho hình bình hành ABCD sở hữu AB = AC. Kéo lâu năm trung tuyến AE của ΔABC và lấy EA = EF. Chứng minh tứ giác ABFC là hình thoi.
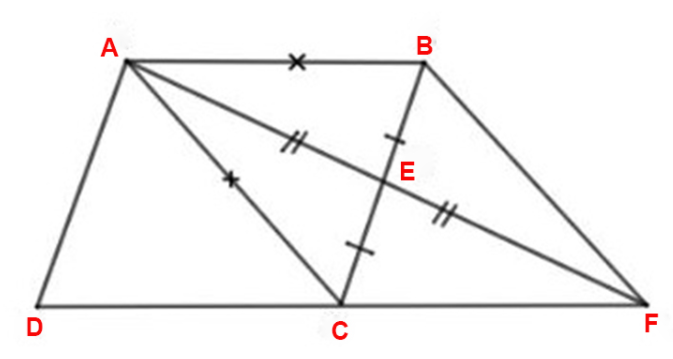
Ta có:
ΔABC cân nặng bên trên A sở hữu trung tuyến AE.
⇒ AE là lối trung trực của BC.
⇒ Tứ giác ABFC là hình thoi bởi sở hữu 2 lối chéo cánh là lối trung trực của nhau.
Cách 3: Hình bình hành sở hữu nhị cạnh kề bởi vì nhau
Ví dụ: Cho tam giác ABC, lấy những điểm D, E theo dõi trật tự bên trên những cạnh AB, AC sao mang đến BD = CE. Gọi M, Phường, Q, O theo lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: MQPO là hình thoi.
Xem thêm: 70+ từ vựng về các phòng trong nhà bằng tiếng Anh
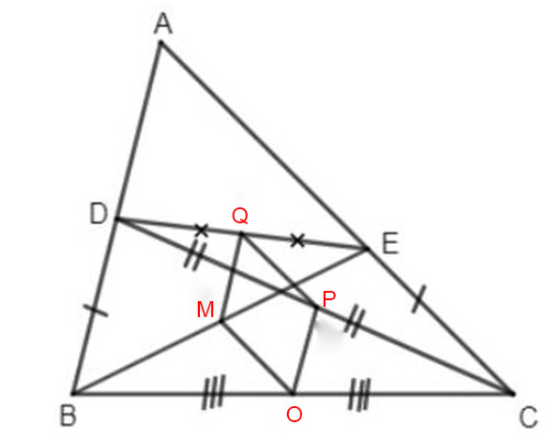
Lời giải
M là trung điểm của BE và Q là trung điểm của DE.
⇒ MQ là lối khoảng của ΔBDE.
⇒ MQ // BD và MQ = ½ BD.
Chứng minh tương tự động, tao có:
PO // BD và PO = ½ BD.
Do sở hữu MQ // PO và MQ = PO nên tứ giác MQPO là hình bình hành (4).
Tương tự động, tao có: QP là lối khoảng của ΔCDE.
⇒ QP = ½ CE tuy nhiên CE = BD (giả thiết) => QM = QP (5).
Từ (4) và (5) ⇒ Tứ giác MQPO là hình thoi bởi là hình bình hành sở hữu nhị cạnh kề đều bằng nhau.
Cách 4: Hình bình hành sở hữu hai tuyến phố chéo cánh vuông góc
Ví dụ: Gọi O là phó điểm hai tuyến phố chéo cánh của hình bình hành ABCD. Chứng minh rằng phó điểm những lối phân giác vô của những tam giác ΔAOB; ΔBOC; ΔCOD và ΔDOA là đỉnh của một hình thoi.
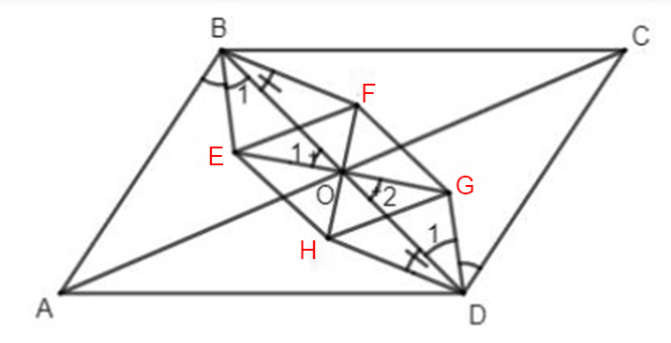
Lời giải:
Gọi E, F, G, H theo lần lượt là phó điểm những phân giác vô của những tam giác AOB, BOC, COD và DOA.
Do O là phó điểm hai tuyến phố chéo cánh AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét ΔBEO và ΔDGO có:
Góc B1 = D1 và Góc O1 = O2 (đối đỉnh) và OB = OD (giả thiết).
=> ΔBEO = ΔDGO (góc cạnh góc).
=> OE = OG và những điểm E, O, G trực tiếp sản phẩm (6).
Chứng minh tương tự: OF = OH và F, O, H trực tiếp sản phẩm (7)
Từ (6) và (7) Suy ra: Tứ giác EFGH là hình bình hành bởi những lối chéo cánh rời nhau bên trên trung điểm từng lối. (8)
Xem thêm: Từ vựng tiếng Anh theo chủ đề Các loài chim - Sylvan Learning Việt Nam
Mặt không giống tao lại sở hữu OE ⊥ OF (là lối phân giác của nhị góc kề bù). (9)
Từ (8) và (9) suy ra: EFGH là hình thoi bởi là hình bình hành sở hữu hai tuyến phố chéo cánh vuông góc.
Hy vọng với những vấn đề tuy nhiên công ty chúng tôi vừa phải share rất có thể gom chúng ta ghi nhớ được khái niệm, tín hiệu phân biệt và đặc thù hình thoi nhé