Hầu như tất cả đề toán nào cũng có sự xuất hiện của đường cao. Vậy đường cao trong tam giác là gì? Các tính chất và công thức tính độ dài của đường cao trong tam giác là gì? Bạn có đủ tự tin để khẳng định rằng mình đã nắm hết các kiến thức này không? Nếu không thì cùng Bamboo School ôn tập lại kiến thức qua bài viết dưới đây nhé!
Định nghĩa đường cao là gì?
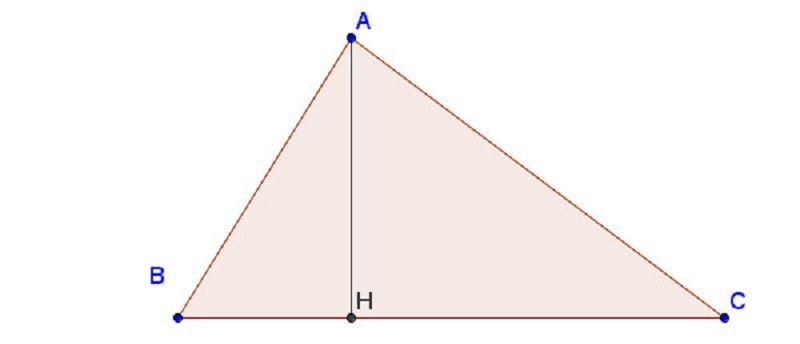
Định nghĩa đường cao trong tam giác
Đường cao của tam giác là đoạn thẳng vuông góc được kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện của tam giác đó.
Cạnh đối diện được gọi là đáy ứng với đường cao đó.
Giao điểm giữa đáy và đường cao được gọi là chân của đường cao.
Độ dài của đường cao được tính bằng khoảng cách từ đỉnh đến đáy.
Trong một tam giác sẽ có 3 đường cao được hạ từ 3 đỉnh của tam giác đó. Ba đường cao này sẽ đồng quy (giao nhau) tại một điểm. Điểm đó được gọi là trực tâm.Tìm hiểu tính chất đường cao trong tam giác
Tính chất đường cao trong tam giác cân
Trong tam giác cân, theo định nghĩa, đường cao tương ứng với cạnh đáy chính là đường trung tuyến ứng với cạnh đáy đó. Như vậy, đường cao của tam giác cân đi qua trung điểm của cạnh đáy.
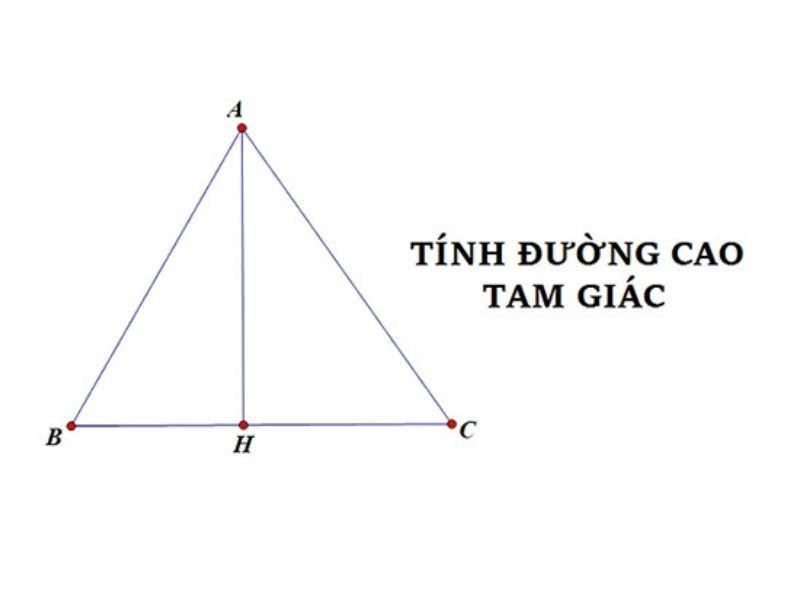
Tính chất đường cao trong tam giác cân
Ngoài ra, đường cao của tam giác cân đồng thời cũng là đường phân giác của góc ở đỉnh và đường trung trực của đáy tam giác. Ngược lại nếu như một tam giác các có đường cao đồng thời cũng là đường trung tuyến hoặc phân giác thì tam giác đó chính là tam giác cân.
Tính chất đường cao trong tam giác vuông
Trong tam giác vuông thì đường cao với đáy là một cạnh góc vuông chính là cạnh góc vuông còn lại. Như vậy thì đỉnh góc vuông chính là chân đường cao hạ từ hai đỉnh còn lại xuống hai cạnh góc vuông của tam giác.
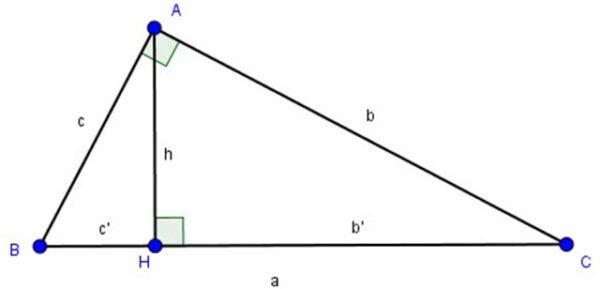
Tính chất đường cao trong tam giác vuông
Tính chất đường cao trong tam giác đều
Tam giác đều là một dạng đặc biệt của tam giác cân. Do đó, tính chất đường cao trong tam giác đều cũng tương tự như tính chất đường cao trong tam giác cân.
Công thức Heron – Công thức tổng quát để tính độ dài đường cao của tam giác thường
Trong đó:
- a,b,c là độ dài ba cạnh của tam giác
- p là nửa chu vi: p=a+b+c2
- ha là độ dài đường cao tương ứng với cạnh đáy a
Ngoài ra, còn có các công thức tính đường cao trong tam giác đặc biệt như sau đây.
Công thức tính đường cao trong tam giác cân
Đường cao trong tam giác cân bằng bình phương độ dài một cạnh của tam giác trừ bình phương độ dài cạnh đáy chia bốn.
Công thức: h2 = a2 − b2/4
Trong đó:
- h: Chiều cao của tam giác cân
- a: Cạnh của tam giác cân
- b: Cạnh đáy tương ứng với chiều cao từ đỉnh của hình tam giác cân
Công thức tính đường cao trong tam giác đều
Nếu bạn đã chắc chắn rằng tam giác này đều, thì đường cao sẽ được tính dựa trên công thức Heron:
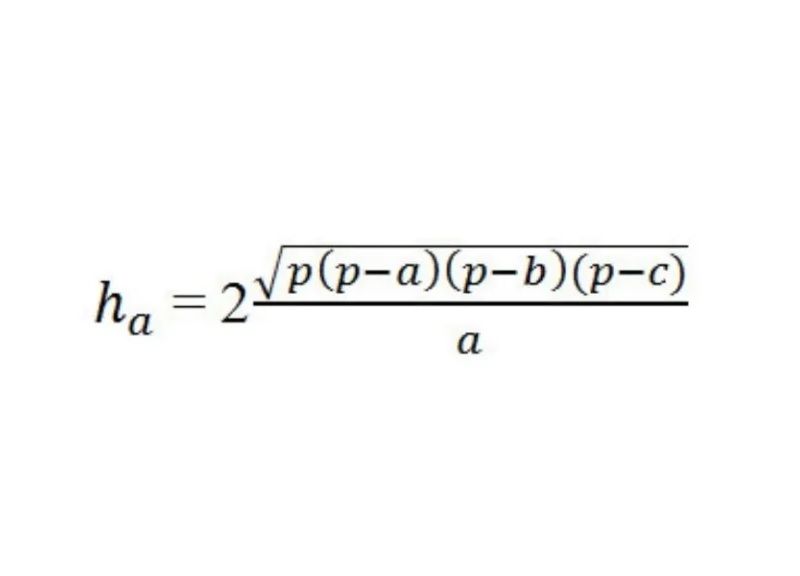
Trong đó:
- a, b, c lần lượt là độ dài của 3 cạnh
- p là nửa chu vi và được tính theo công thức: p= (a+b+c)/2
Công thức tính đường cao trong tam giác vuông
Công thức tính đường cao trong tam giác vuông có thể tính theo:
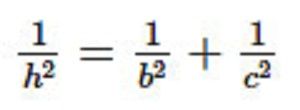
Trong đó:
- a, b, c lần lượt là độ dài 2 cạnh góc vuông
- h là chiều cao kẻ từ góc vuông đến cạnh huyền
Tìm hiểu về trực tâm tam giác
Ngoài định nghĩa về đường cao trong tam giác, trực tâm cũng là thứ mà các học sinh nên lưu ý.
Định nghĩa trực tâm là gì?
Trực tâm của tam giác hiểu đơn giản chính là giao của ba đường cao xuất phát từ ba đỉnh của tam giác đó, đồng thời vuông góc với cạnh đối diện. Ba đường cao này sẽ giao nhau tại một điểm, ta gọi đó là trực tâm của tam giác.
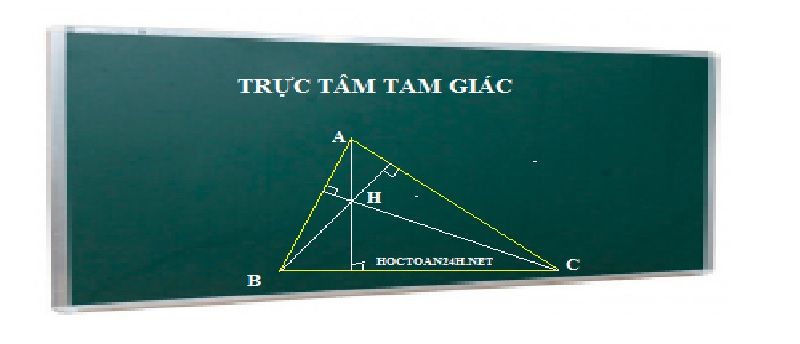
Giả sử cho tam giác LMN có ba đường cao lần lượt là LP, MQ, NI. Gọi S là là giao điểm của ba đường cao trên thì S là trực tâm của tam giác LMN.
Tính chất trực tâm tam giác
Có 5 tính chất trực tâm tam giác như sau:
- Trong một tam giác cân thì đường trung trực tương ứng với cạnh đáy sẽ đồng thời là đường phân giác, đường cao và đường trung tuyến của tam giác đó.
- Trong một tam giác, nếu như một đường trung tuyến đồng thời là đường phân giác thì tam giác đó sẽ là tam giác cân.
- Trong một tam giác, nếu như một đường trung tuyến đồng thời là đường trung trực thì tam giác đó sẽ là tam giác cân.
- Trực tâm của tam giác nhọn ABC sẽ trùng với tâm của đường tròn nội tiếp tam giác có ba đỉnh là chân của ba đường cao từ các đỉnh A, B, C đến các cạnh đối diện BC, AC, AB tương ứng.
- Đường cao tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại một điểm thứ hai sẽ là đối xứng của trực tâm qua cạnh tương ứng.
Ví dụ về tính độ dài đường cao trong tam giác
Cho tam giác ABC vuông tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE?
Bài giải:
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có ∠A = ∠E = 90o
∠C chung
=> Tam giác ACB ∾ tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
Trên đây là những kiến thức về đường cao trong tam giác mà chắc hẳn các bạn sẽ cần dùng đến khi ôn thi. Hy vọng bài viết này từ cuongthinhcorp.com.vn sẽ là nguồn tham khảo hữu ích trong quá trình học tập của các bạn.