Chắc hẳn các bạn học sinh đôi lúc sẽ gặp khó khăn với các câu hỏi Thế nào là tam giác cân? Sự khác nhau giữa tam giác cân và tam giác đều? Tính chất tam giác vuông cân là gì?. Để trả lời cho các câu hỏi đó GiaiToan.com xin giới thiệu đến bạn đọc tài liệu Tam giác vuông, tam giác cân, tam giác đều. Hy vọng đây sẽ là tài liệu hữu ích cho các em học sinh lớp 7 ôn tập và nâng cao kiến thức môn Toán 7.
A. Tam giác là gì?
- Tam giác là hình gồm ba cạnh AB, AC, BC được tạo thành từ ba điểm A, B, C không thẳng hàng.
Cách vẽ tam giác
Bước 1: Vẽ ba điểm A, B, C không thẳng hàng trên mặt giấy.
Bước 2: Nối các điểm A với B, B với C, C với A.
Ta nhận được kết quả như sau:
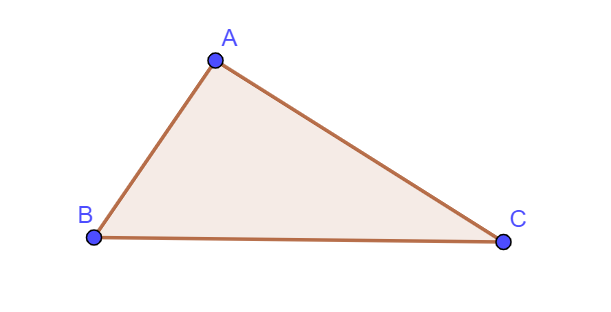
B. Tam giác cân
1. Định nghĩa tam giác cân
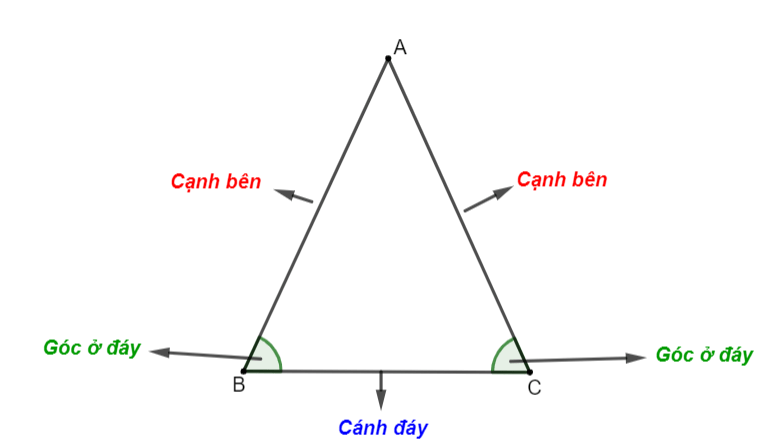
- Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên.
- Đỉnh của một tam giác cân là giao điểm của hai cạnh bên.
- Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy.
Ví dụ: Cho tam giác ABC cân tại A
2. Tính chất tam giác cân
Tính chất 1: Trong một tam giác cân hai góc ở đáy bằng nhau.
Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân.
Tính chất 3: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.
Tính chất 4: Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.
3. Dấu hiệu nhận biết tam giác cân
Dấu hiệu 1: Nếu một tam giác có hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.
Dấu hiệu 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
C. Tam giác đều
1. Định nghĩa tam giác đều
- Tam giác đều là tam giác có ba cạnh bằng nhau.
2. Tính chất tam giác đều
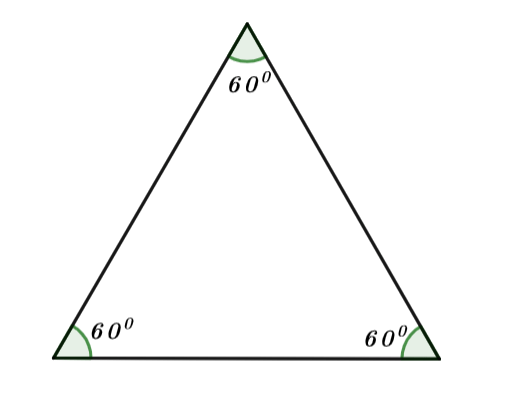 Tính chất 1: Ba góc bằng nhau và bằng 600.
Tính chất 1: Ba góc bằng nhau và bằng 600.
Tính chất 2: Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Tính chất 3: Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều
Tính chất 4: Trong một tam giác đều, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.
3. Dấu hiệu nhận biết tam giác đều
Dấu hiệu 1: Tam giác có ba cạnh bằng nhau là tam giác đều
Dấu hiệu 2: Tam giác có ba góc bằng nhau là tam giác đều
Dấu hiệu 3: Tam giác cân có một góc bằng 600
Dấu hiệu 4: Tam giác có hai góc bằng 600 là tam giác đều
D. Tam giác vuông, Tam giác vuông cân
- Tam giác vuông là tam giác có một góc bằng 900
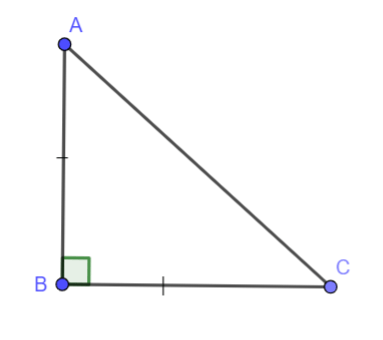
1. Định nghĩa tam giác vuông cân
- Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân.
(Hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau)
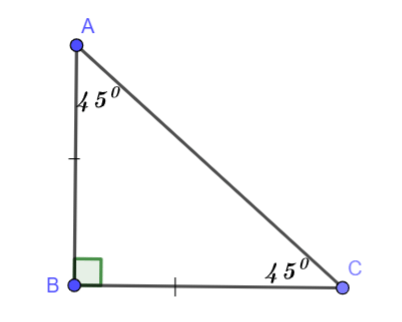
- Tam giác ABC có AB = AC, A B ⊥ A C thì tam giác ABC vuông cân tại A.
2. Tính chất tam giác vuông cân
Tính chất 1: Tam giác vuông cân có hai góc nhọn ở đáy bằng nhau và bằng 450
Tính chất 2: Các đường cao, đường trung tuyến, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
3. Cách chứng minh tam giác vuông cân
Để chứng minh một tam giác là tam giác vuông cân ta chứng minh một tam giác có:
- Hai cạnh góc vuông bằng nhau.
- Tam giác vuông có một góc bằng 450
- Tam giác cân có một góc ở đáy bằng 450
E. Chứng minh tam giác
Bài 1: Cho tam giác ABC có H là trực tâm, G là trọng tâm và O là giao điểm của ba đường trung trực. Chứng minh rằng HG = 2GO.
Bài 2: Cho tam giác ABC nhọn góc A bằng 450, các đường cao BD và CE cắt nhau tại J. Gọi I là trung điểm của DE, G là trọng tâm tam giác ABC. Chứng minh rằng ba điểm H, G, I thẳng hàng.
Bài 3: Cho tam giác ABC vuông tại A, vẽ ra phía ngoài tam giác đó các tam giác ABD vuông cân tại B, tam giác ACF vuông cân tại C. Gọi H là giao điểm của AB và CD, K là giao điểm của AC và BF. Chứng minh rằng: AH = AK
Bài 4: Cho tam giác ABC có BC < BA. Qua C kẻ đường thẳng vuông góc với tia phân giác BE của góc ABC và đường thẳng này cắt BE tại F và cắt trung tuyến BD tại G. Chứng minh rằng đoạn thẳng EG bị đoạn thẳng DF chia làm hai phần bằng nhau.
Bài 5: Cho tam giác ABC không cân. Gọi D là trung điểm của BC, gọi AE và AF lần lượt là đường phân giác trong và phân giác ngoài của tam giác ABC. Gọi H là hình chiếu của A trên BC. Chứng minh rằng EF.GH = AB.AC
Bài 6: Cho tam giác ABC có I là giao điểm ba đường phân giác và D, E lần lượt là trung điểm của AC và AB. Đường thẳng DI cắt AB tại Q và đường thẳng EI cắt AC tạo P. Biết rằng diện tích tam giác ABC bằng diện tích tam giác APQ. Tính số đo góc BAC.
Bài 7: Cho tam giác ABC có BC = 2AB, M là trung điểm của BC, D là trung điểm của BM. Chứng minh rằng: AC = 2AD
Bài 8: Cho tam giác ABC cân tại A có góc A < 900. Kẻ BD vuông góc với AC. Trên AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
a) DE // BC
b) CE vuông góc với AB.
------------------------------------------------------
Hy vọng tài liệu trên sẽ giúp các em học sinh ghi nhớ lý thuyết về tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng hơn. Chúc các em học tốt.