Toán Tiểu học: Công thức tính diện tích, chu vi, thể tích hình cơ bản giúp các em học sinh lớp 4, 5, hệ thống hóa kiến thức về tính diện tích, tính chu vi, thể tích hình tam giác, hình tứ giác, hình vuông, hình chữ nhật, hình tròn, hình bình hành, hình thoi, hình nón, hình cầu, hình trụ, hình lập phương, hình thang, hình hộp chữ nhật.
Qua đó, các em dễ dàng áp dụng vào từng bài tập cụ thể, mà không gặp bất kỳ trở ngại nào, để ngày càng học tốt phần Hình học. Mời các em cùng theo dõi bài viết dưới đây của Download.vn để nắm vững các công thức hình học cơ bản nhé:
- 1. Tính chu vi, diện tích Hình chữ nhật
- Công thức tính chu vi Hình chữ nhật
- Công thức tính diện tích Hình chữ nhật
- 2. Tính chu vi, diện tích Hình vuông
- Công thức tính chu vi Hình vuông
- Công thức tính diện tích Hình vuông
- 3. Tính chu vi, diện tích Hình bình hành
- Công thức tính chu vi Hình bình hành
- Công thức tính diện tích Hình bình hành
- 4. Tính chu vi, diện tích Hình thoi
- Công thức tính chu vi Hình thoi
- Công thức tính diện tích Hình thoi
- 5. Tính chu vi, diện tích Hình tam giác
- Công thức tính chu vi Hình tam giác
- Công thức tính diện tích Hình tam giác
- 6. Tính chu vi, diện tích Hình tứ giác
- Công thức tính chu vi Hình tứ giác
- Công thức tính diện tích Hình tứ giác
- 7. Tính chu vi, diện tích Hình thang vuông, cân
- Công thức tính chu vi hình thang
- Công thức tính diện tích hình thang
- 8. Tính chu vi, diện tích hình tròn
- Công thức tính chu vi hình tròn
- Công thức tính diện tích hình tròn
- 9. Tính diện tích, thể tích hình lập phương
- Tính diện tích xung quanh hình lập phương
- Tính diện tích toàn phần hình lập phương
- Tính thể tích hình lập phương
- 10. Tính diện tích, thể tích hình hộp chữ nhật
- Tính diện tích xung quanh hình hộp chữ nhật
- Tính diện tích toàn phần hình hộp chữ nhật
- Tính thể tích hình hộp chữ nhật
- 11. Tính diện tích, thể tích hình nón
- Công thức tính diện tích xung quanh hình nón
- Công thức tính diện tích toàn phần hình nón
- Công thức tính thể tích hình nón
- 12. Tính diện tích, thể tích hình trụ
- Công thức tính diện tích xung quanh hình trụ
- Công thức tính diện tích toàn phần hình trụ
- Công thức tính thể tích hình trụ
- 13. Tính chu vi, diện tích Hình cầu
- Công thức tính diện tích mặt cầu
- Công thức tính thể tích hình cầu
1. Tính chu vi, diện tích Hình chữ nhật

Công thức tính chu vi Hình chữ nhật
Công thức: P = (a + b) x 2.
Muốn tính chu vi hình chữ nhật, ta lấy chiều dài cộng chiều rộng nhân với 2 (cùng một đơn vị đo).
Mở rộng: Biết chu vi tính cạnh bằng cách lấy nửa chu vi (P : 2) trừ cạnh đã biết.
Công thức tính diện tích Hình chữ nhật
Công thức: S = a x b.
Muốn tính diện tích hình chữ nhật, ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo).
Mở rộng: Biết DT tìm cạnh bằng cách lấy DT chia cạnh đã biết.
2. Tính chu vi, diện tích Hình vuông

Công thức tính chu vi Hình vuông
Công thức: P = a x 4
Muốn tính chu vi hình vuông, ta lấy độ dài một cạnh nhân với 4.
Mở rộng: Nếu biết chu vi hình vuông, để tìm cạnh hình vuông ta lấy chu vi hình vuông chia 4.
Công thức tính diện tích Hình vuông
Công thức: S = a x a.
Muốn tính diện tích hình vuông, ta lấy độ dài một cạnh nhân với chính nó.
Mở rộng: Nếu biết diện tích hình vuông, ta có thể tìm cạnh hình vuông bằng cách nhẩm.
3. Tính chu vi, diện tích Hình bình hành
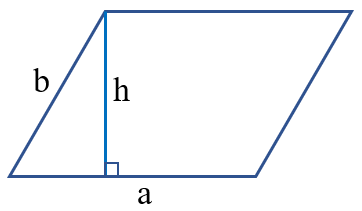
Công thức tính chu vi Hình bình hành
Công thức: P = (a + b) x 2
Muốn tính chu vi hình bình hành, ta lấy tổng hai cạnh kề nhân với 2 (cùng một đơn vị đo).
Mở rộng: Biết chu vi tính cạnh bằng cách lấy nửa chu vi (P : 2) trừ cạnh đã biết.
Công thức tính diện tích Hình bình hành
Công thức: S = a x h
Muốn tính diện tích hình bình hành, ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
Mở rộng: Biết diện tích hình bình hành, ta có thể tính:
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
4. Tính chu vi, diện tích Hình thoi
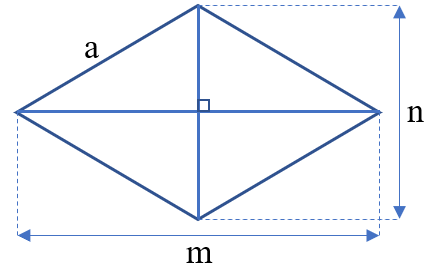
Công thức tính chu vi Hình thoi
Công thức: P = a x 4
Muốn tính chu vi hình thoi, ta lấy độ dài cạnh hình thoi nhân với 4.
Mở rộng: Nếu biết chu vi hình thoi, để tìm cạnh hình thoi ta lấy chu vi chia 4.
Công thức tính diện tích Hình thoi
Công thức: S = ![]()
Muốn tính diện tích hình thoi, ta lấy tích độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo).
5. Tính chu vi, diện tích Hình tam giác
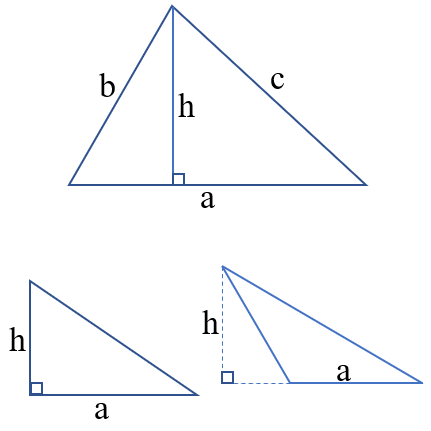
Công thức tính chu vi Hình tam giác
Công thức: C = a + b + c
Muốn tính chu vi hình tam giác, ta lấy độ dài 3 cạnh tam giác cộng lại với nhau (cùng một đơn vị đo).
Mở rộng: Nếu biết chu vi hình tam giác và 2 cạnh, ta tìm cạnh còn lại bằng cách lấy chu vi trừ đi tổng 2 cạnh còn lại: a = C - (b+c).
Công thức tính diện tích Hình tam giác
Công thức: S = ![]()
Muốn tính diện tích hình tam giác, ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2 (cùng một đơn vị đo).
Mở rộng: Nếu ta biết diện tích hình tam giác, ta có thể tính:
- Chiều cao: h = (S x 2) : a
- Cạnh đáy: a = (S x 2) : h
6. Tính chu vi, diện tích Hình tứ giác
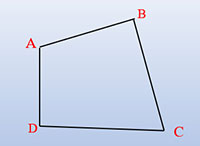
Công thức tính chu vi Hình tứ giác
Công thức: P = a + b + c + d
Trong đó:
P là chu vi hình tứ giác
a, b, c, d lần lượt là độ dài các cạnh của tứ giác
Công thức tính diện tích Hình tứ giác
Sẽ không có công thức chung để tính diện tích hình tứ giác mà chúng ta dựa vào cụ thể hình tứ giác đó là gì để có cách tính diện tích khác nhau.
7. Tính chu vi, diện tích Hình thang vuông, cân
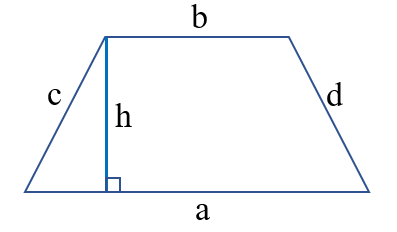
Có một cạnh bên vuông góc với hai đáy, cạnh bên đó chính là chiều cao hình thang vuông. Khi tính diện tích hình thang vuông ta tính như cách tìm hình thang.
Hình thang cân: có hai đường chéo bằng nhau, hai góc tù bằng nhau và hai góc nhọn bằng nhau.
Công thức tính chu vi hình thang
Công thức: C = a + b + c + d
Muốn tính chu vi hình thang, ta lấy độ dài các cạnh hình thang cộng lại với nhau (cùng một đơn vị đo).
Mở rộng: Nếu biết chu vi hình thang và độ dài 3 cạnh, ta có thể tìm cạnh còn lại bằng cách lấy chu vi trừ đi tổng độ dài 3 cạnh: a = C - (b + c + d).
Công thức tính diện tích hình thang
Công thức: S = ![]()
Muốn tính diện tích hình thang, ta lấy tổng độ dài hai đáy nhân với chiều cao rồi đem chia cho 2 (cùng một đơn vị đo).
Mở rộng: Nếu biết diện tích hình thang, ta có thể tính
- Chiều cao: h = (S x 2) : a
- Cạnh đáy: a = (S x 2) : h
8. Tính chu vi, diện tích hình tròn
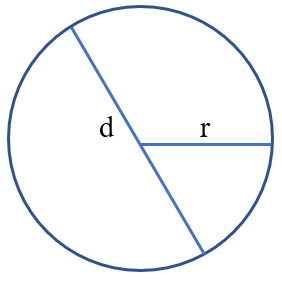
Công thức tính chu vi hình tròn
Công thức: C = d x 3,14
hoặc r x 2 x 3,14
Muốn tính chu vi hình tròn, ta lấy đường kính nhân với số 3,14 (hoặc lấy bán kính nhân 2 rồi nhân với 3,14).
Mở rộng: Nếu biết chu vi hình tròn, ta có thể tính:
- Đường kính: d = C : 3,14
- Bán kính: r = C : 3,14 : 2
Công thức tính diện tích hình tròn
Công thức: r x r x 3,14
Muốn tính diện tích hình tròn, ta lấy bán kinh nhân với bán kính rồi nhân với số 3,14.
9. Tính diện tích, thể tích hình lập phương
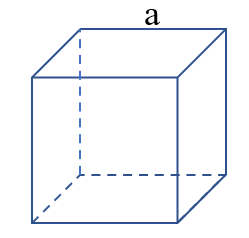
Tính diện tích xung quanh hình lập phương
Công thức: Sxq = Sm x 4
Muốn tính diện tích xung quanh, ta lấy diện tích 1 mặt của hình lập phương nhân với 4.
Tính diện tích toàn phần hình lập phương
Công thức: Stp = Sm x 6
Muốn tính diện tích xung quanh, ta lấy diện tích 1 mặt của hình lập phương nhân với 6.
Tính thể tích hình lập phương
Công thức: V = a x a x a
Muốn tính thể tích hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
10. Tính diện tích, thể tích hình hộp chữ nhật
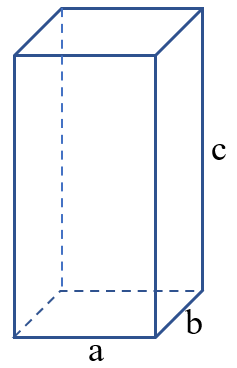
Tính diện tích xung quanh hình hộp chữ nhật
Công thức: Sxq = P x c
Muốn tính diện tích xung quanh của hình hộp chữ nhật, ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
Tính diện tích toàn phần hình hộp chữ nhật
Công thức: Stp = Sxq + Sđ x 2
Muốn tính diện tích toàn phần của hình hộp chữ nhật, ta lấy diện tích xung quanh của hình hộp chữ nhật cộng với 2 lần diện tích đáy (cùng một đơn vị đo).
Tính thể tích hình hộp chữ nhật
Công thức: V = a x b x c
Muốn tính thể tích của hình hộp chữ nhật, ta lấy chiều rài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
11. Tính diện tích, thể tích hình nón
Công thức tính diện tích xung quanh hình nón
Diện tích xung quanh hình nón được xác định bằng tích của hằng số Pi (π) nhân với bán kính đáy hình nón (r) nhân với đường sinh hình nón (l). Đường sinh có thể là một đường thẳng hoặc 1 đường cong phẳng. Với hình nón thì đường sinh có chiều dài từ mép của vòng tròn đến đỉnh của hình nón.
![]()
Trong đó:
- Sxq: là ký hiệu diện tích xung quanh hình nón.
- π: là hằng số Pi có giá trị xấp xỉ là 3,14
- r: Bán kính mặt đáy hình nón và bằng đường kính chia 2 (r = d/2).
- l: đường sinh của hình nón.
Công thức tính diện tích toàn phần hình nón
Diện tích toàn phần hình nón bằng diện tích xung quanh hình nón cộng với diện tích mặt đáy hình nón. Vì diện tích mặt đáy là hình tròn nên áp dụng công thức tính diện tích hình tròn là Sđ = π.r.r.
![]()
Công thức tính thể tích hình nón
Để tính được thể tích hình nón ta áp dụng công thức sau:
![]()
Trong đó:
- V: Ký hiệu thể tích hình nón
- π: là hằng số = 3,14
- r: Bán kính hình tròn đáy.
- h: là đường cao hạ từ đỉnh xuống tâm đường tròn đáy.
12. Tính diện tích, thể tích hình trụ
Công thức tính diện tích xung quanh hình trụ
S (xung quanh) = 2 x π x r x h
Trong đó:
- r: bán kính hình trụ
- h: chiều cao nối từ đáy tới đỉnh hình trụ
- π = 3,14
Công thức tính diện tích toàn phần hình trụ
S (toàn phần) = 2 x π x r2 + 2 x π x r x h = 2 π x r x (r + h)
Trong đó:
- r: bán kính hình trụ
- 2 x π x r x h: diện tích xung quanh hình trụ
- 2 x π x r2: diện tích của hai đáy
Công thức tính thể tích hình trụ
V = π x r2 x h
Trong đó:
- r: bán kính hình trụ
- h: chiều cao hình trụ
13. Tính chu vi, diện tích Hình cầu
Công thức tính diện tích mặt cầu
![]()
Công thức tính thể tích hình cầu

Trong đó:
- S là diện tích mặt cầu
- V là thể tích hình cầu
- r là bán kính mặt cầu/hình cầu
- d là bánh kính mặt cầu/hình cầu