Có 2 cách tính góc giữa hai đường thẳng là sử dụng công thức tính vô hướng của 2 véc tơ và dựng tam giác chứa góc sau đó áp dụng các định lý cosin để tính.

Bài viết này được đăng tại cuongthinhcorp.com.vn, không được copy dưới mọi hình thức.
Góc giữa hai đường thẳng là một kiến thức hết sức cơ bản nhưng cũng đóng vai trò quan trọng trong việc giải các bài tập hình học của chương trình toán lớp 10. Trong bài viết hôm nay, hãy cùng freetuts ôn tập lại các kiến thức liên quan cũng như cách tính góc tạo bởi hai đường thẳng nha.
Lý thuyết góc giữa hai đường thẳng
Khái niệm góc giữa hai đường thẳng trong không gian
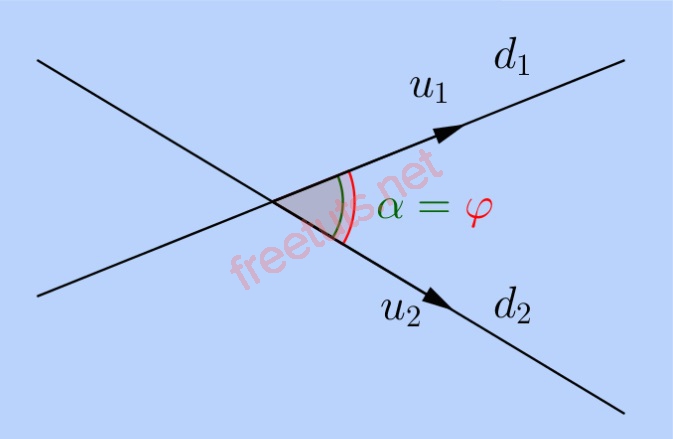
Alpha là kí hiệu góc giữa hai đường thẳng d1 và d2.
Trong không gian, góc giữa hai đường thẳng là góc được tạo bởi hai đường thẳng d1 và d2 thỏa mãn số đo 0 90.
Góc tạo bởi hai đường thẳng chính là góc giữa hai vecto chỉ phương hoặc hai vecto pháp tuyến của d1 và d2.
Bài viết này được đăng tại [free tuts .net]
Điều kiện để có góc tạo bởi hai đường thẳng
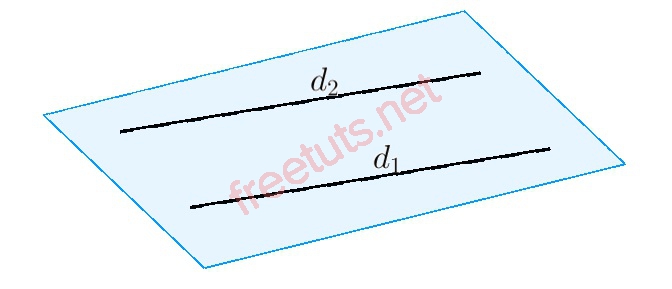
Góc giữa hai đường thẳng song song bằng 0 độ.
Để xuất hiện góc ở giữa hai đường thẳng thì hai đường thẳng này phải là hai đường thẳng không trùng nhau, không song song và cắt nhau tại 1 điểm. Vì nếu hai đường thẳng song song hoặc trùng nhau thì góc tạo bởi 2 chúng là 0 độ hay nói cách khác là không tồn tại góc tạo bởi 2 đường thẳng này.
Ứng dụng việc tính góc giữa hai đường thẳng trong thực tế
Trong thực tế, việc tính góc tạo bởi hai đường thẳng có rất nhiều ứng dụng như:
- Định vị trong hệ thống GPS: Việc tính góc tạo bởi hai đường thẳng sẽ cung cấp thông tin chính xác về hướng và khoảng cách từ vị trí bất kỳ đến điểm đích.
- Trong xây dựng, việc tính góc giữa 2 đường thẳng giúp đo đạc chính xác và xác định hướng.
- Trong không gian 3 chiều, tính góc tạo bởi 2 đường thẳng giúp xác định mối tương quan giữa các đối tượng và hình dạng không gian của chúng.
- Trong công nghệ điều hướng, tính góc tạo bởi hai đường thẳng sẽ giúp xác định phương hướng di chuyển và qua đó giúp điều khiển các phương tiện.
Cách xác định góc giữa hai đường thẳng
Để xác định góc giữa 2 đường thẳng d và d’, các em hãy làm theo các bước sau:
- Bước 1: Lấy điểm O thuộc một trong hai đường thẳng d hoặc d’
- Bước 2: Từ O, vẽ một đường thẳng song song với đường thẳng còn lại
- Bước 3: Lấy u là vecto chỉ phương của đường thẳng d, v là vecto chỉ phương của đường thẳng d’, (u,v) = , vậy góc giữa 2 đường thẳng d và d’ = , nếu 0 90 độ.
Cách tính góc giữa hai đường thẳng chuẩn nhất
Các em đã hiểu thế nào là góc giữa 2 đường thẳng và cách xác định chúng rồi đúng không nào, bây giờ hãy cùng tìm hiểu cách tính góc tạo bởi 2 đường thẳng nha.
Áp dụng tích vô hướng của 2 véc tơ
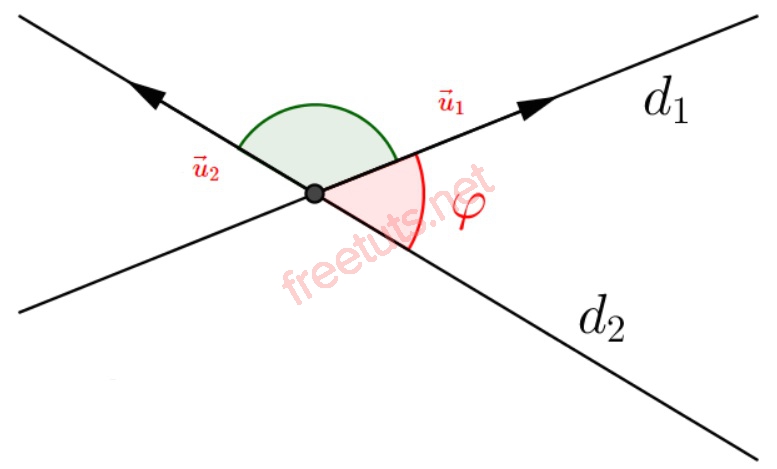
Góc tạo bởi hai đường thẳng d1, d2.
Cho hệ trục tọa độ Oxy, và hai đường thẳng d1, d2.
Gọi véc tơ u(a,b,c), v(a',b',c') là 2 véc tơ chỉ phương của d1 và d2.
Lúc này, ta có công thức tính góc giữa hai đường thẳng trong không gian như sau:
Cos(d1,d2) = |cos(u1,u2)| = |u1.u2|/|u1|.|u2|
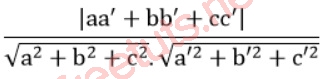
Với 0 90 độ.
Ví dụ minh họa:
Tính cosin góc tạo bởi đường thẳng d với trục Ox, biết:
d: (x + 3)/2 = (y - 1)/1 = (z - 2)/1
Lời giải:
Với d = d: (x + 3)/2 = (y - 1)/1 = (z - 2)/1,
Ta có, véc tơ chỉ phương của d = ud=(2; 1; 1)
Véc tơ chỉ phương trục Ox là Ox =(1; 0; 0)
Vậy cos góc giữa d và Ox là:
cos = |ud.Ox|/(|ud|.|Ox|)
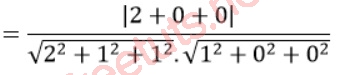
= 2/6 = 6 /3.
Vậy cos = 6 /3.
Dựng tam giác chứa góc và tính
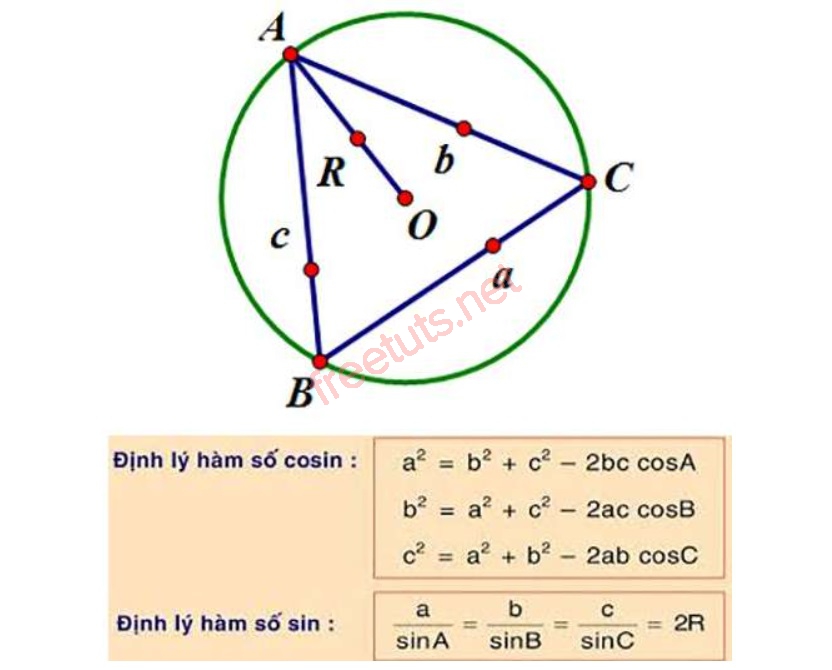
Định lý hàm số sin, cosin trong tam giác.
Có một cách khá đơn giản để tính góc tạo bởi 2 đường thẳng đó chính là các em hãy dựng một hình tam giác chứa góc cần tính và áp dụng các định lý cosin trong tam giác này để có thể tính ra số đo của góc cần tìm.
Ví dụ minh họa: Cho hình chóp S.ABC, SA = SB = SC = AB = a, AC = a2, BC = a3, SAC vuông góc tại S. Tính cos góc tạo bởi hai đường thẳng SC và AB.
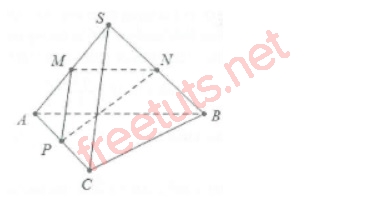
Hình chóp S.ABC
Lời giải:
Gọi M, N, P lần lượt là trung điểm của 3 cạnh SA, SB, AC, lúc này, ta có:
MN // SC, N // AB, suy ra góc tạo bởi (SC, AB) = góc tạo bởi (MP; MN).
Vì tam giác SAB là tam giác cân, nên MN = AB/2 = a/2; MP = SC/2 = a/2.
Vì SAC là tam giác vuông tại S, nên SP = ½.AC = (a2)/2.
BP^2 = (BA^2 + BC^2)/2 - AC^2/4 = 3/2.a^2 BP = (a6)/2.
PN^2 = (PS^2 + PB^2)/2 - SB^2/4 = 3a^2/4 PN = (a3)/2.
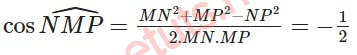
cos(góc NMP) = 120 độ góc NMP bằng 60 độ.
Vậy góc tạo bởi đường thẳng SC và AB bằng 60 độ.
Bài tập tính góc giữa hai đường thẳng
Như vậy, các em đã nắm vững lý thuyết góc giữa 2 đường thẳng và phương pháp tính góc này rồi đúng không nào, bây giờ hãy cùng vận dụng chúng để giải một số bài tập sau nha.
- Bài 1: Cho tứ diện ABCD, biết: AB = 2, AC = 4, AD = BC = 5, BD = 3, CD = 6, tính góc tạo bởi 2 đường thẳng AC và BD.
Lời giải:
Ta có:
cos(AC.AB) = (AC.AB)/AC.BD = AC(AD-AB)/(AC.BD) = (AC.AD- AC.AB)/(AC.BD)
= (AC2 + BC2 - CD22 - AC2 + AB2 - BC22)/(AC.BD) = AD2 + BC2 - CD2 - AB22.AC.BD = 5/12
Vậy góc tạo bởi hai đường thẳng AC và BD = arccos 5/12 = 65 độ.
- Bài 2: Cho đường thẳng d: (z + 1)/3 = (y - 0)/5 = (z - 2)/2, tính góc tạo bởi d và trục Ox.
Lời giải:
Với d: (z + 2)/3 = (y - 1)/5 = (z - 2)/2, ta có:
Véc tơ chỉ phương của đường thăng d là ud=(3; 5; 2)
Véc tơ chỉ phương trục Ox là Ox =(1; 0; 0)
Gọi là góc tạo bởi d và Ox, ta có:
Cos = |ud.Ox|/(|ud|.|Ox|) = |3.1 + 5.0 + 2.0|/32+52+ 22.12+02+ 02 = 338/38
góc = 1,06 rad xấp xỉ 60 độ.
Vậy góc tạo bởi đường thẳng d và trục Ox là 60 độ.
Như vậy, qua bài viết trên, cuongthinhcorp.com.vn đã giúp các em ôn tập lại kiến thức góc giữa hai đường thẳng và cách xác định cũng như các cách tính góc tạo bởi 2 đường thẳng một cách đầy đủ và chi tiết nhất. Hy vọng đây sẽ là những kiến thức bổ ích đối với các em học sinh lớp 10, chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi nha.