• Tìm kiếm

Lý thuyết hai tam giác đồng dạng | SGK Toán lớp 8


1. Định nghĩa Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

I. Các kiến thức cần nhớ

Định nghĩa:

Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.

Ví dụ: $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Chú ý: 

* Tỉ số các cạnh tương ứng \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}} = k\) được gọi là tỉ số đồng dạng  của hai tam giác.

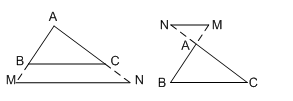
Định lí về tạo ra hai tam giác đồng dạng

Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì  nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Cho $\Delta ABC$, $MN{\rm{//}}BC$

$ \Rightarrow \Delta AMN$$\backsim$$\Delta ABC.$

Chú ý: Định lí cũng đúng trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.

II. Các dạng toán thường gặp

Dạng 1: Sử dụng tam giác đồng dạng để tính độ dài cạnh, chu vi, tỉ số đồng dạng, số đo góc…

Phương pháp:

Ta sử dụng định nghĩa và định lý về hai tam giác đồng dạng. Sử dụng định lý Ta-lét và tính chất tỉ lệ thức để tính toán.

$\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Dạng 2: Sử dụng tam giác đồng dạng để chứng minh các yếu tố hình học (hai đường thẳng song song, …)

Phương pháp:

Ta sử dụng $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Và định lý:  Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì  nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.


Bình luận

Chia sẻ

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.