Hình chóp tứ giác đều - Tìm hiểu về đặc tính và ứng dụng
Chủ đề Hình chóp tứ giác đều: Hình chóp tứ giác đều là một khái niệm quan trọng trong toán học, và việc hiểu sâu về nó sẽ giúp chúng ta phát triển tư duy logic và khả năng giải quyết vấn đề. Hình chóp tứ giác đều được tạo thành từ một hình vuông đáy và các tam giác cân bằng nhau. Điều đặc biệt là đỉnh của chóp đi qua tâm đáy, tạo nên một hình học thú vị và hấp dẫn.
Hình chóp tứ giác đều là một hình chóp mà hình đáy của nó là một tứ giác đều. Đặc điểm của hình chóp tứ giác đều bao gồm:
1. Đáy là tứ giác đều: Mọi cạnh và góc nội tiếp của hình đáy đều bằng nhau. Điều này có nghĩa là độ dài cạnh của hình đáy và các góc nội tiếp của nó đều được chia đều và bằng nhau.
2. Các cạnh bên là tam giác cân bằng nhau: Các cạnh của các tam giác bên (hay cạnh bên) của hình chóp đều có độ dài bằng nhau. Điều này có nghĩa là chiều cao của các tam giác bên sẽ cắt các cạnh bên vào điểm trung điểm, tạo thành các đoạn thẳng bằng nhau.
3. Các cạnh bên gặp tại một đỉnh chung: Các cạnh bên của hình chóp tứ giác đều gặp nhau tại một đỉnh chung, được gọi là đỉnh của hình chóp.
4. Chiều cao của hình chóp đi qua tâm đáy: Đường cao của hình chóp tứ giác đều đi qua tâm của hình đáy. Đường cao được hình thành bởi sự giao nhau của đường chéo hình vuông, nối hai đỉnh không kề nhau của hình vuông đáy.
5. Các mặt phẳng bên của hình chóp tứ giác đều đi qua tâm hình đáy: Mỗi mặt phẳng bên của hình chóp tứ giác đều cắt hình đáy của nó tại điểm trung điểm của các cạnh của hình đáy.
Tóm lại, hình chóp tứ giác đều có đáy là một tứ giác đều, các cạnh bên là các tam giác cân bằng nhau, và các mặt phẳng bên đi qua tâm của đáy.
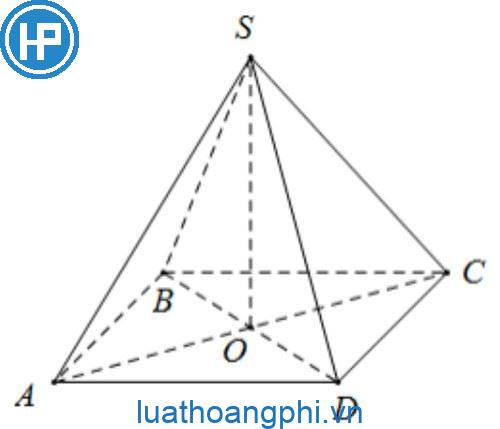
Hình chóp tứ giác đều là gì?
Hình chóp tứ giác đều là một hình chóp có đáy là một hình vuông và các mặt bên là các tam giác đều, với đỉnh của chóp đi qua tâm của đáy (giao của hai đường chéo của hình vuông).
Để tạo ra một hình chóp tứ giác đều, chúng ta có thể làm như sau:
1. Bắt đầu bằng một hình vuông với các cạnh bằng nhau. Điểm này sẽ là tâm của đáy của chóp.
2. Kế tiếp, vẽ các đường thẳng từ các đỉnh của đáy của hình vuông đến đỉnh của chóp. Các đường thẳng này cắt nhau tại một điểm duy nhất, và đây chính là đỉnh của chóp tứ giác đều.
3. Tiếp theo, vẽ các cạnh của chóp bằng cách nối từ đỉnh của chóp đến các điểm trên các cạnh của đáy.
4. Cuối cùng, bạn có một hình chóp tứ giác đều với đáy là một hình vuông và các mặt bên là các tam giác đều.
Hình chóp tứ giác đều có các tính chất đặc biệt, bao gồm các góc giữa các mặt bên là các góc cân, và tất cả các cạnh và đỉnh của chóp đều nằm trên một mặt phẳng duy nhất.
Hi vọng rằng thông tin này đã giúp bạn hiểu rõ về hình chóp tứ giác đều.
Có bao nhiêu mặt bên trong một hình chóp tứ giác đều?
Một hình chóp tứ giác đều có bao nhiêu mặt bên phụ thuộc vào số đỉnh của hình vuông đáy.
Công thức tổng quát để tính số mặt bên của một hình chóp tứ giác đều là số đỉnh của hình vuông đáy trừ đi 1. Vì một hình vuông có 4 đỉnh, nên số mặt bên của một hình chóp tứ giác đều là 4 - 1 = 3.
Vậy nếu hình vuông đáy của hình chóp tứ giác đều có 4 đỉnh thì hình chóp đó sẽ có 3 mặt bên.
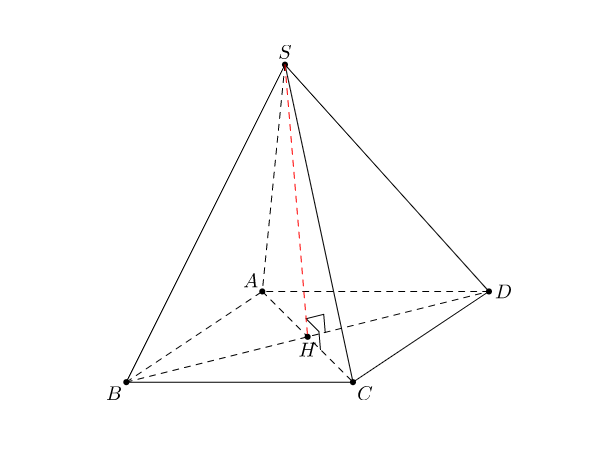
Hình chóp tứ giác đều có đặc điểm gì về các cạnh của nó?
Hình chóp tứ giác đều có đặc điểm về các cạnh như sau:
1. Cạnh đáy: Hình chóp tứ giác đều có cạnh đáy là một hình vuông. Mỗi cạnh của hình vuông đều có độ dài bằng nhau.
2. Cạnh bên: Hình chóp tứ giác đều có các cạnh bên là các tam giác đều. Mỗi cạnh của các tam giác đều có độ dài bằng nhau.
3. Cạnh đỉnh: Hình chóp tứ giác đều có cạnh đỉnh là đường thẳng nối đỉnh của chóp với tâm của đáy hình vuông.
Tổng kết lại, các cạnh của hình chóp tứ giác đều đều có độ dài bằng nhau, gồm cạnh đáy là hình vuông và các cạnh bên là các tam giác đều.
Tâm chóp của một hình chóp tứ giác đều nằm ở đâu?
Tâm chóp của một hình chóp tứ giác đều nằm ở tâm đáy của hình vuông đáy. Đường cao của chóp đi qua tâm đáy, cắt đường chéo của hình vuông đáy tại giao điểm. Tâm chóp cũng là giao điểm của hai đường chéo hình vuông đáy. Do đó, tâm chóp của một hình chóp tứ giác đều nằm ở trung điểm của hai đường chéo hình vuông đáy.
_HOOK_
Toán 8 - CT MỚI - HÌNH CHÓP TỨ GIÁC ĐỀU - THẦY KENKA
Những hình chóp tứ giác đều là những sáng tạo tuyệt đẹp của toán học. Xem video này và khám phá vẻ đẹp hình học của chúng đồng thời hiểu rõ hơn về các đặc điểm và tính năng của hình chóp tứ giác đều.
Toán 8 - Cánh Diều - Chương 4 - Bài 2 - Hình chóp tứ giác đều - Tiết 1
Bạn đã từng thấy cánh diều lượn bay trong trời xanh chưa? Video này sẽ đưa bạn vào cuộc hành trình tưởng như không giới hạn để khám phá vẻ đẹp và sự phiêu lưu của cánh diều. Cùng xem ngay để hòa mình vào khám phá không gian mênh mông.
Làm thế nào để tính diện tích mặt đáy của một hình chóp tứ giác đều?
Để tính diện tích mặt đáy của một hình chóp tứ giác đều, ta cần biết cạnh của hình vuông đáy (cảnh của một tam giác đều bên), và công thức tính diện tích hình vuông.
Bước 1: Gọi c là cạnh của hình vuông đáy, có thể là độ dài cạnh của một tam giác đều bên.
Bước 2: Tính diện tích của một hình vuông bằng cách lấy cạnh của nó và nhân với chính nó: diện tích = c x c = c^2.
Ví dụ, nếu c = 5, ta sẽ có diện tích của mặt đáy là 5^2 = 25 đơn vị diện tích.
Đường cao của hình chóp tứ giác đều có đặc điểm gì đặc biệt?
Đường cao của hình chóp tứ giác đều có các đặc điểm sau:
1. Đường cao của hình chóp tứ giác đều là đoạn thẳng nối từ đỉnh của chóp đến tâm của đáy hình vuông. Vì đáy hình vuông làm cho đường cao của chóp đi qua tâm đáy, nghĩa là đường cao cắt đáy đúng tại tâm đáy.
2. Đường cao của hình chóp tứ giác đều có thể được coi như là phương chiếu của đỉnh chóp lên mặt đáy hình vuông. Điều này có nghĩa là đỉnh chóp được chiếu vuông góc lên mặt đáy.
3. Đường cao của hình chóp tứ giác đều cắt mặt bên của chóp thành hai tam giác cân bằng nhau. Điều này có nghĩa là đường cao chia đều mặt bên của chóp thành hai phần bằng nhau, và hai phần này là hai tam giác có cạnh và góc đỉnh đồng nhất.
4. Đường cao của hình chóp tứ giác đều cũng là trục đối xứng của hình chóp tứ giác đều. Điều này có nghĩa là nếu ta xoay chóp quanh đường cao, chóp sẽ giữ nguyên hình dáng.
Với các đặc điểm nổi bật như trên, đường cao của hình chóp tứ giác đều đóng vai trò quan trọng trong việc xác định hình dạng và cấu trúc của chóp.
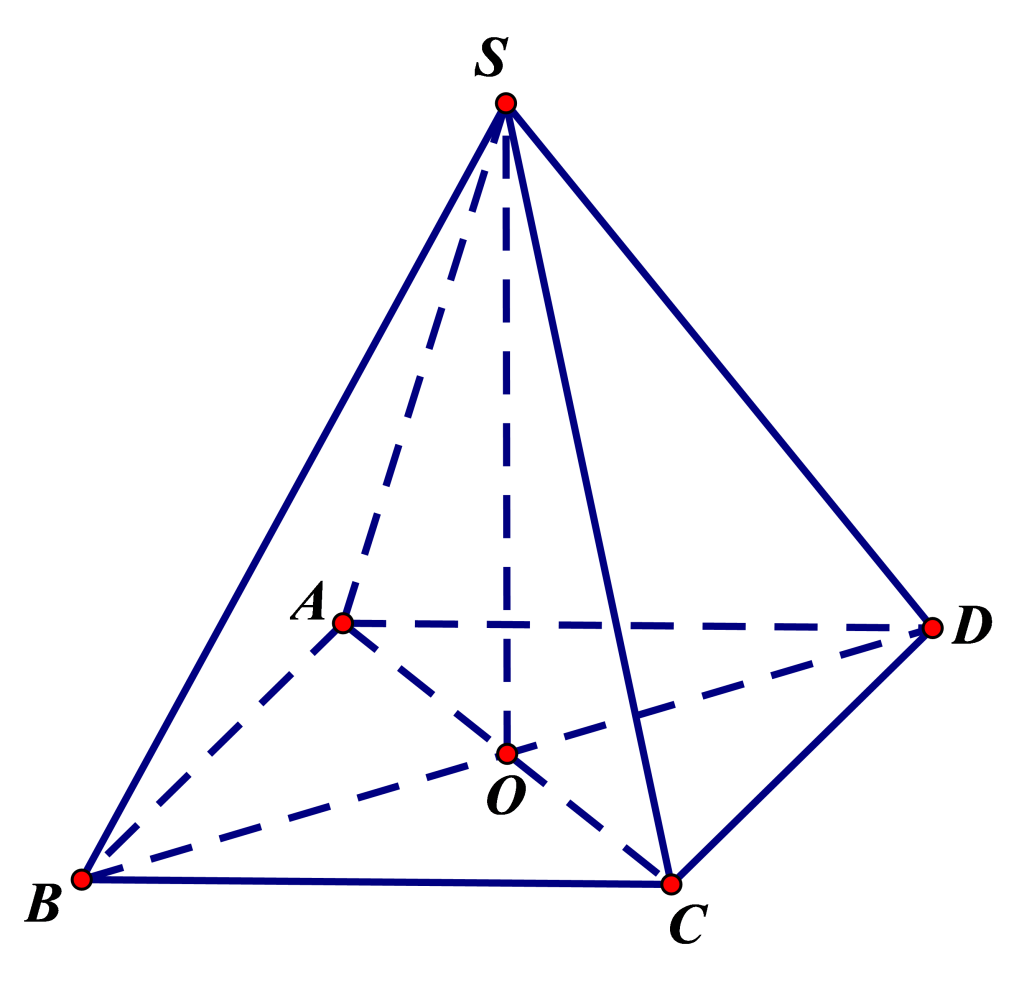
Hình chóp tứ giác đều có bao nhiêu điểm đối xứng?
Hình chóp tứ giác đều có 1 điểm đối xứng.
Để hiểu rõ hơn, chúng ta cần biết định nghĩa của hình chóp tứ giác đều. Hình chóp tứ giác đều là một loại hình chóp có đáy là một hình vuông, và đường cao của chóp đi qua tâm của đáy. Điểm đối xứng trong trường hợp này là điểm ở tâm đáy.
Điểm đối xứng là điểm mà nếu bạn vẽ một đường thẳng qua điểm đó, hình ảnh của hình đối xứng qua đường thẳng đó là hoàn toàn trùng khớp với hình gốc. Trong trường hợp này, nếu chúng ta vẽ một đường thẳng qua tâm đáy của hình chóp tứ giác đều, hình ảnh của hình chóp qua đường thẳng này sẽ hoàn toàn trùng khớp với hình chóp gốc.
Vì vậy, hình chóp tứ giác đều có 1 điểm đối xứng, đó là điểm ở tâm đáy.
Toán 8 - Chân trời sáng tạo - Bài 1: Hình chóp tam giác đều - Hình chóp tứ giác đều (HAY NHẤT)
Chân trời sáng tạo là nơi mà khả năng tưởng tượng và sáng tạo không có giới hạn. Xem video này để khám phá những ý tưởng mới và độc đáo, cùng với những bước tiến sáng tạo trong công nghệ, nghệ thuật và khoa học.
Công thức tính thể tích của hình chóp tứ giác đều là gì?
Công thức tính thể tích của hình chóp tứ giác đều là:
V = (1/3) * S * h
Trong đó:
- V là thể tích của hình chóp tứ giác đều.
- S là diện tích đáy của hình chóp tứ giác đều.
- h là chiều cao của hình chóp tứ giác đều.
Để tính được thể tích của hình chóp tứ giác đều, ta cần biết diện tích đáy và chiều cao của chóp. Diện tích đáy có thể được tính bằng công thức S = a^2, trong đó a là độ dài cạnh đáy của hình vuông. Chiều cao của chóp có thể tính bằng công thức h = sqrt(3) * a/2, trong đó a là độ dài cạnh đáy của hình vuông.
Sau khi tính được diện tích đáy và chiều cao của hình chóp tứ giác đều, ta có thể áp dụng công thức trên để tính thể tích của nó.

Mối quan hệ giữa đường cao và cạnh đáy của hình chóp tứ giác đều là gì?
Mối quan hệ giữa đường cao và cạnh đáy của hình chóp tứ giác đều là gì?
Trong hình chóp tứ giác đều, đường cao của chóp là đoạn thẳng nối đỉnh chóp với trung điểm cạnh đáy. Cạnh đáy của hình chóp tứ giác đều là đoạn thẳng nối hai đỉnh liền kề trên đáy.
Mối quan hệ giữa đường cao và cạnh đáy của hình chóp tứ giác đều là rằng đường cao chia đôi cạnh đáy và cắt nhau ở góc 90 độ. Nghĩa là, đường cao cắt cạnh đáy ở trung điểm của cạnh đáy và tạo ra hai đoạn thẳng có chiều dài bằng nhau.
Điều này có nghĩa là đường cao của hình chóp tứ giác đều là một đường trung tuyến và cũng là đường phân giác của tam giác đáy.
Tóm lại, trong hình chóp tứ giác đều, đường cao chia đôi cạnh đáy và tạo thành hai đoạn thẳng có chiều dài bằng nhau.
_HOOK_
Tại sao hình chóp tứ giác đều được gọi là đều?
Hình chóp tứ giác đều được gọi là \"đều\" vì nó có các đặc điểm sau đây:
1. Các cạnh của mặt đáy của hình chóp tứ giác đều cùng độ dài: Điều này có nghĩa là các cạnh của hình vuông đáy đều có độ dài như nhau.
2. Các cạnh của các tam giác bên của hình chóp tứ giác đều cùng độ dài và các tam giác này cũng cân bằng nhau: Điều này đồng nghĩa với việc các cạnh của các tam giác bên đều có độ dài bằng nhau và các tam giác này cũng có các góc và đỉnh tương tự nhau.
3. Đường cao của hình chóp tứ giác đều đi qua tâm đáy: Điểm giao của hai đường chéo của hình vuông đáy được gọi là tâm đáy. Đường cao của hình chóp tứ giác đều đi qua tâm đáy này.
Với các đặc điểm trên, hình chóp tứ giác đều có các phần tử bên trong nó đều tương đương và đồng nhất, tạo thành một hình dạng đồng đều và đẹp mắt.
Toán 8 - Cánh Diều - Chương 4 - Bài 1 - Hình chóp tam giác đều - Tiết 1
Hình chóp tam giác đều là một trong những hình dạng đáng ngạc nhiên và đẹp trong hình học. Xem video này để hiểu rõ hơn về các tính chất và ứng dụng của hình chóp tam giác đều, cũng như cách chúng được tạo ra và sử dụng trong thế giới thực.
Làm thế nào để vẽ hình chóp tứ giác đều?
Để vẽ hình chóp tứ giác đều, chúng ta có thể làm theo các bước sau:
Bước 1: Vẽ hình vuông đáy
- Vẽ một đoạn thẳng đứng làm đoạn cơ sở của hình vuông đáy.
- Từ hai đầu của đoạn thẳng đứng, vẽ hai đoạn thẳng ngang cùng độ dài, là hai cạnh còn lại của hình vuông đáy.
- Kết nối các đầu mút của các đoạn thẳng ngang lại với nhau bằng các đoạn thẳng đứng, tạo thành hình vuông đáy.
Bước 2: Xác định đỉnh của chóp
- Vẽ hai đường chéo của hình vuông đáy sao cho chúng giao nhau ở một điểm tạo thành đỉnh của chóp.
- Đỉnh của chóp đi qua tâm của hình vuông đáy, nghĩa là là đoạn nối từ đỉnh chóp tới tâm đáy vuông góc với đường chéo.
Bước 3: Vẽ các cạnh bên
- Kết nối đỉnh của chóp với các đỉnh của hình vuông đáy bằng các đoạn thẳng, tạo thành các cạnh bên của chóp.
Bước 4: Tô màu hoặc đánh dấu các phần của hình chóp
- Nếu bạn muốn tô màu cho hình chóp, bạn có thể tô màu các tam giác của các mặt bên và đáy.
- Bạn cũng có thể đánh dấu các đỉnh và cạnh của hình chóp để làm nổi bật hình ảnh.
Hy vọng với các bước trên, bạn sẽ có thể vẽ được hình chóp tứ giác đều một cách dễ dàng.
Tính chất của các tam giác bên trong hình chóp tứ giác đều là gì?
Hình chóp tứ giác đều là một hình chóp có đáy là một hình vuông và các mặt bên là các tam giác cân. Để tính chất của các tam giác bên trong hình chóp tứ giác đều, ta có một số điểm sau:
1. Tất cả các tam giác bên trong hình chóp tứ giác đều đều cân.
- Điều này có nghĩa là độ dài các cạnh tạo thành các tam giác bên của hình chóp là bằng nhau.
- Cụ thể, ta có thể gọi a là độ dài cạnh của đáy (hình vuông), thì độ dài các cạnh của các tam giác bên cũng đều bằng a.
2. Hai tam giác bên cạnh nhau trong hình chóp tứ giác đều là đồng dạng.
- Điều này có nghĩa là các cặp tam giác bên cạnh nhau có các góc tương ứng bằng nhau và các cạnh tương ứng có tỉ lệ bằng nhau.
- Vì các tam giác bên trong hình chóp tứ giác đều cân, nên các góc và tỉ lệ cạnh tương ứng của chúng đều bằng nhau.
3. Phân giác của một góc tại đỉnh của tam giác đều trong hình chóp tứ giác đều là đường cao.
- Điều này có nghĩa là đường đi qua tâm đáy (giao của các đường chéo hình vuông) cắt các góc tươi của các tam giác bên thành các phân giác góc tại đỉnh.
- Đây cũng chính là đường cao của các tam giác bên.
Như vậy, đó là một số tính chất căn bản về các tam giác bên trong hình chóp tứ giác đều. Điều này đồng nghĩa với việc các tam giác bên đều có các cạnh và góc tương ứng bằng nhau.

Hình chóp tứ giác đều có bao nhiêu trạng thái tồn tại?
Hình chóp tứ giác đều có 2 trạng thái tồn tại:
1. Trạng thái tròn: Khi đường cao của chóp đi qua tâm đáy (giao của 2 đường chéo hình vuông), hình chóp tứ giác đều sẽ tạo thành một hình tròn trong mặt đáy. Các mặt bên của chóp sẽ là các tam giác đều.
2. Trạng thái vuông: Khi đỉnh của chóp không nằm trên đường cao đi qua tâm đáy, mà nằm ngoài hình tròn đáy. Trong trạng thái này, các mặt bên của chóp sẽ được hình thành từ các tam giác cân bằng nhau.
Đây là hai trạng thái tồn tại của hình chóp tứ giác đều.
Ứng dụng của hình chóp tứ giác đều trong cuộc sống là gì?
Ứng dụng của hình chóp tứ giác đều trong cuộc sống là rất đa dạng và phong phú. Dưới đây là một số ví dụ về việc áp dụng hình chóp tứ giác đều trong thực tế:
1. Kiến trúc: Hình chóp tứ giác đều được sử dụng rộng rãi trong thiết kế và xây dựng các công trình kiến trúc. Ví dụ, trong kiến trúc truyền thống của Ai Cập cổ đại, các đại diện của hình chóp tứ giác đều là các kim tự tháp nổi tiếng, như Kim tự tháp Khufu ở Giza.
2. Quảng cáo: Hình chóp tứ giác đều cũng được sử dụng trong lĩnh vực quảng cáo. Với hình dạng độc đáo và thu hút, các hình chóp tứ giác đều thường được tạo thành từ các tấm hợp kim hoặc các tấm banner để quảng bá sản phẩm hoặc dịch vụ.
3. Giáo dục: Hình chóp tứ giác đều cũng được sử dụng trong giáo dục để giúp học sinh nắm vững kiến thức về không gian và hình học. Việc nghiên cứu và vẽ hình chóp tứ giác đều giúp học sinh phát triển kỹ năng tư duy, tăng cường khả năng hình dung và tư duy không gian.
4. Mô phỏng: Trong một số lĩnh vực như thực tế ảo và đồ họa máy tính, hình chóp tứ giác đều được sử dụng để tạo ra các mô phỏng và hình ảnh 3D. Các phần mềm và công cụ thiết kế đồ họa sử dụng hình chóp tứ giác đều để biểu diễn các đối tượng và không gian 3 chiều.
5. Vật lý: Trong Vật lý, hình chóp tứ giác đều được sử dụng để mô phỏng và giải thích các hiện tượng vật lý, như ánh sáng phản xạ và khúc xạ thông qua các mô hình hình chóp tứ giác đều.
Trên đây chỉ là một số ví dụ về ứng dụng của hình chóp tứ giác đều trong cuộc sống. Hình chóp tứ giác đều có nhiều ứng dụng khác nữa và chúng có vai trò quan trọng trong nhiều lĩnh vực.
_HOOK_
Bài 1: Hình chóp tam giác đều - Hình chóp tứ giác đều (P1)
Tạo dáng, không gian và vẻ ngoài đặc biệt là những yếu tố tạo nên sự nổi bật của hình chóp tam giác đều. Video này sẽ đưa bạn vào cuộc phiêu lưu để khám phá những hình chóp tam giác đều độc đáo và ấn tượng nhất. Đừng bỏ lỡ cơ hội xem ngay!