Hình thang cân toán lớp 8 |Toán 8 chương trình mới

Trong công tác toán 8 liên kết trí thức, chân mây phát minh, cánh diều những em sẽ tiến hành học tập những kiến thức và kỹ năng về hình thang cân nặng. Bài ghi chép sau đây tiếp tục tổ hợp kiến thức và kỹ năng những em cần thiết bắt vô bài bác hình thang cân nặng toán lớp 8. Mời những em nằm trong theo gót dõi.

1. Khái niệm hình thang và hình thang cân

- Hình thang là tứ giác với nhị cạnh đối tuy nhiên song cùng nhau.

Bạn đang xem: Hình thang cân toán lớp 8 |Toán 8 chương trình mới

Ví dụ: Tứ giác ABCD với AB // CD => ABCD là hình thang.

- Hình thang cân nặng là hình thang với nhị góc kề một lòng cân nhau.

Ví dụ: Hình thang ABCD có 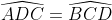$\widehat{ADC}=\widehat{BCD}$ => ABCD là hình thang cân nặng.

2. Tính hóa học của hình thang cân

- Định lý 1: Trong hình thang cân nặng, nhị cạnh mặt mày cân nhau.

- Định lý 2: Trong hình thang cân nặng, hai tuyến đường chéo cánh cân nhau.

Ví dụ: Hình thang cân nặng ABCD với AD = BC ; AC = BD

3. Dấu hiệu nhận ra hình thang cân

- Định lý 3: Nếu một hình thang với hai tuyến đường chéo cánh cân nhau thì hình thang này đó là hình thang cân nặng.

Ví dụ: Hình thang ABCD (AB // CD) có 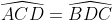$\widehat{ACD}=\widehat{BDC}$ . Chứng minh ABCD là hình thang cân nặng.

Hai lối chéo cánh AC và BD hạn chế nhau bên trên O.

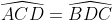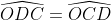Do $\widehat{ACD}=\widehat{BDC}$ nên $\Delta$ OCD có $\widehat{ODC}=\widehat{OCD}$ => $\Delta$ OCD cân nặng.

=> OC = OD (1).

Chứng minh tương tự động tao có 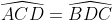$\widehat{ACD}=\widehat{BDC}$ và AB // CD => $\Delta$ OAB cân nặng bên trên O

=> OA = OB (2)

Từ (1) và (2) => OA + OC = OB + OD => AC = BD

=> Hình thang ABCD với hai tuyến đường chéo cánh AC = BD => ABCD là hình thang cân nặng.

>> Xem thêm: Tổng thích hợp kiến thức và kỹ năng toán 8 cụ thể SGK mới

4. Bài tập luyện hình thang cân toán lớp 8 công tác mới

4.1 Bài tập luyện hình thang cân nặng sách toán 8 liên kết tri thức

Bài 3.4 trang 55 SGK toán 8/1 liên kết tri thức

ABCD là hình thang => AB // CD

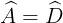=> $\large \widehat{A}=\widehat{D}$ = 180^o => $\large \widehat{D}$ = 180^o - $\large \widehat{A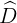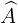}$ = 180^o - 120^o = 60^o

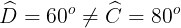
=> $\large \widehat{D}=60^{o}\neq \widehat{C}=80^{o}$

=> ABCD ko nên là hình thang cân nặng.

Bài 3.5 trang 55 SGK toán 8/1 liên kết tri thức

Xét ∆ DOE và ∆ COE có:

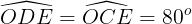$\large \widehat{ODE}=\widehat{OCE}=80^{o}$ =90° (vì OD ⊥ DE; OC ⊥ CE);

EC = ED (giả thiết);

Cạnh OE chung

Do ê ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

=> OC = OD (hai cạnh tương ứng) (1)

Do ê tam giác OCD cân nặng bên trên O nên 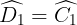$\large \widehat{D_{1}}=\widehat{C_{1}}$ .

Vì ABCD là hình thang nên AB // CD suy ra 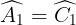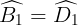$\large \widehat{A_{1}}=\widehat{C_{1}}$ ; $\large \widehat{B_{1}}=\widehat{D_{1}}$ (cặp góc sánh le trong).

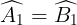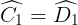=> $\large \widehat{A_{1}}=\widehat{B_{1}}$ (do $\large \widehat{C_{1}}=\widehat{D_{1}}$ )

Suy đi ra ∆ OAB cân nặng bên trên O nên OA = OB (2)

Ta có: AC = OA + OC và BD = OB + OD (3)

Từ (1), (2) và (3) suy đi ra AC = BD

Hình thang ABCD với AC = BD nên ABCD là hình thang cân nặng.

Bài 3.6 trang 55 SGK toán 8/1 liên kết tri thức

Cách vẽ hình thang cân nặng ABCD với lòng rộng lớn CD nhiều năm 4 centimet, cạnh mặt mày nhiều năm 2 centimet và lối chéo cánh nhiều năm 3 cm:

– Vẽ cạnh CD = 4 centimet.

– Dùng compa vẽ hai tuyến đường tròn xoe (D; 2 cm) và (C; 3 cm). Hai lối tròn xoe này hạn chế nhau bên trên điểm A.

– Dùng compa vẽ hai tuyến đường tròn xoe (D; 3 cm) và (C; 2 cm). Hai lối tròn xoe này hạn chế nhau bên trên điểm B.

– Nối AB, AD, BC tao được hình thang cân nặng ABCD (như hình vẽ).

Bài 3.7 trang 55 SGK toán 8/1 liên kết tri thức

Có ABCD là hình thang cân nặng nên 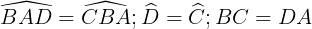$\large \widehat{BAD}=\widehat{CBA};\widehat{D}=\widehat{C}; BC = DA$

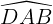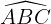
Ta với EA và EB phen lượng là lối phân giác của $\large \widehat{DAB}$ và $\large \widehat{ABC}$

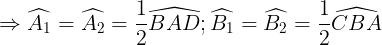
$\large \Rightarrow \widehat{A_{1}}=\widehat{A_{2}}=\frac{1}{2}\widehat{BAD};\widehat{B_{1}}=\widehat{B_{2}}=\frac{1}{2}\widehat{CBA}$

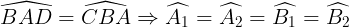
Mà $\large \widehat{BAD}=\widehat{CBA}\Rightarrow \widehat{A_{1}}=\widehat{A_{2}}=\widehat{B_{1}}=\widehat{B_{2}}$

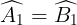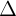Ta có $\large \widehat{A_{1}}=\widehat{B_{1}}$ => $\large \Delta$ BEA cân nặng bên trên E => AE = BE.

Xét 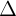$\large \Delta$ EAD và 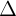$\large \Delta$ EBC có:

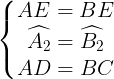
$\large \left\{\begin{matrix} AE=BE & & \\ \widehat{A_{2}}=\widehat{B_{2}}& & \\ AD = BC & & \end{matrix}\right.$

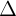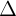=> $\large \Delta$ EAD = $\large \Delta$ EBC

=> EC = ED.

Bài 3.8 trang 55 SGK toán 8/1 liên kết tri thức

•Vì ABCD là hình thang cân nặng nên 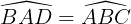$\large \widehat{BAD}=\widehat{ABC}$ ; AD = BC; AC = BD.

Xét DICD cân nặng bên trên I, vì 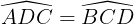$\large \widehat{ADC}=\widehat{BCD}$ nên IC = ID.

=> IC – BC = ID – AD, hoặc IB = IA

Do ê I cơ hội đều A và B nên I phía trên lối trung trực của AB (1)

•Xét ∆ABD và ∆BAC có:

AB là cạnh chung;

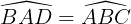$\large \widehat{BAD}=\widehat{ABC}$ (chứng minh trên);

AD = BC (chứng minh trên).

Do ê ∆ABD = ∆BAC (c.g.c)

Suy đi ra 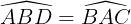$\large \widehat{ABD}=\widehat{BAC}$ (hai góc tương ứng).

Tam giác JAB cân nặng bên trên J vì 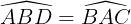$\large \widehat{ABD}=\widehat{BAC}$ nên JA = JB

Do ê J cơ hội đều A và B nên J phía trên lối trung trực của AB (2)

Từ (1) và (2) => I, J nằm trong phía trên đường thẳng liền mạch IJ là lối trung trực của đoạn trực tiếp AB.

4.2 Bài tập luyện hình thang cân nặng sách toán 8 chân mây sáng sủa tạo

Bài 1 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

Ta với AB // DC nên tứ giác ABCD là hình thang

Do ê 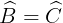$\large \widehat{B}=\widehat{C}$ =180°

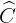=> x = $\large \widehat{C}$ = 180° $\large \widehat{B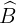}$ = 180°−140° =40°

Ta với MN // PQ nên tứ giác MNPQ là hình thang

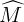Do đó $\large \widehat{M}+\widehat{Q}$ = 180°

=> $\large \widehat{M}$ =180°− $\large \widehat{Q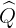}$ = 180°−60°= 120°.

Ta có $\large \widehat{N_{1}}+\widehat{N_{2}}=180^{o}$

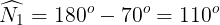
=> $\large \widehat{N_{1}}=180^{o}-70^{o}=110^{o}$

Ta có $\large \widehat{M} + \widehat{N} + \widehat{P}+\widehat{Q}=360^{o}$

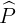=> $\large \widehat{P}$ = 360^o- 110^o- 60^o - 120^o = 70^o

Ta với HG // IK nên tứ giác GHIK là hình thang.

$\large \Rightarrow \left\{\begin{matrix} x+4x=180^{o} & \\ 2x+3x=180^{o}& \end{matrix}\right.\Leftrightarrow 5x=180^{o}\Rightarrow x=36^{o}$

Ta với VS ⊥ ST và UT ⊥ ST nên VS // UT.

Do ê tứ giác STUV là hình thang

Suy đi ra $\large \widehat{U}+\widehat{V}$ =180°

Nên 2x + x = 180° hoặc 3x = 180°, suy đi ra x = 60°.

Bài 2 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

Xét DABD với AB = AD nên là 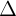$\large \Delta$ cân nặng bên trên A

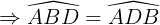
$\large \Rightarrow \widehat{ABD}=\widehat{ADB}$

Vì BD là tia phân giác của góc B nên 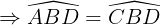$\large \Rightarrow \widehat{ABD}=\widehat{CBD}$ (tính hóa học tia phân giác của một góc)

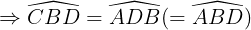
$\large \Rightarrow \widehat{CBD}=\widehat{ADB}(=\widehat{ABD})$

Mà nhị góc này ở địa điểm sánh le vô nên AD // BC.

Xét tứ giác ABCD với AD // BC nên là hình thang => ABCD là hình thang.

Bài 3 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

a) Ta với AH ⊥ BC, AH ⊥ NM nên BC // NM

Tứ giác BCMN với BC // NM nên là hình thang.

b) Do BC // NM nên 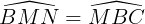$\large \widehat{BMN}=\widehat{MBC}$ (so le trong).

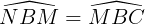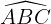Mà $\large \widehat{NBM}=\widehat{MBC}$ (do BM là tia phân giác của $\large \widehat{ABC}$ )

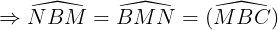
$\large \Rightarrow \widehat{NBM}=\widehat{BMN}=(\widehat{MBC})$

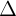$\large \Delta$ BMN có 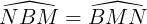$\large \widehat{NBM}=\widehat{BMN}$ nên là 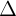$\large \Delta$ cân nặng bên trên N

=> BN = MN.

Bài 4 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

a) Xét ∆ABD và ∆EBD có:

BA = BE (giả thiết);

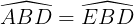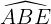$\large \widehat{ABD}=\widehat{EBD}$ (do BD là tia phân giác của $\large \widehat{ABE}$ );

BD là cạnh công cộng,

Do ê ∆ABD = ∆EBD (c.g.c).

b) Do ∆ABD = ∆EBD (câu a) nên 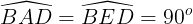$\large \widehat{BAD}=\widehat{BED}=90^{o}$ (hai góc tương ứng).

Do ê DE ⊥ BC

Mà AH ⊥ BC (giả thiết) nên DE // AH.

Tứ giác ADEH với DE // AH nên là hình thang

Lại với 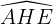$\large \widehat{AHE}$ = 90° nên ADEH là hình thang vuông.

c) Do ∆ABD = ∆EBD (câu a) nên AD = ED (hai cạnh tương ứng)

Do ê D phía trên lối trung trực của AE.

Lại với BA = BE (giả thiết) nên B phía trên lối trung trực của AE.

=> BD là lối trung trực của đoạn trực tiếp AE nên BD ⊥ AE, hoặc BI ⊥ AE.

Xét ∆ABE với AI ⊥ BE, BI ⊥ AE nên I là trực tâm của tam giác

Do ê EI ⊥ AB hoặc EF ⊥ AB.

Mà CA ⊥ AB (do ∆ABC vuông bên trên A)

=> EF // CA.

Tứ giác ACEF với EF // CA nên là hình thang.

Lại có 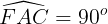$\large \widehat{FAC}=90^{o}$ nên ACEF là hình thang vuông.

Bài 5 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

Ta thấy nhị góc kề một lòng của tứ giác GHIK với số đo là 51° và 129° ko cân nhau.

Do ê tứ giác GHIK ko nên là hình thang cân nặng.

Ta có $\large \widehat{Q_{1}}+\widehat{MQP}=180^{o}$ (hai góc kề bù) nên

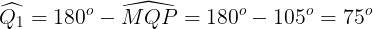
$\large \widehat{Q_{1}}=180^{o}-\widehat{MQP}=180^{o}-105^{o}=75^{o}$

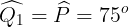
Do đó $\large \widehat{Q_{1}}=\widehat{P}=75^{o}$

Mà nhị góc này ở địa điểm đồng vị nên MQ // NP.

Xem thêm: b%C3%B3ng%20%C4%91%C3%A8n trong Tiếng Anh, dịch

Tứ giác MNPQ với MQ // NP nên là hình thang.

Do MQ // NP nên 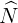$\large \widehat{N}$ =75° (góc N sánh le vô với góc ngoài bên trên đỉnh M của hình thang)

Do ê 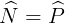$\large \widehat{N}=\widehat{P}$ =75°.

=> Hình thang MNPQ là hình thang cân nặng bởi với 2 góc kề lòng cân nhau.

Bài 6 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

Do ABCD là hình thang cân nặng nên AB // DC và AD = BC; AC = BD; 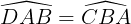$\large \widehat{DAB}=\widehat{CBA}$ (tính hóa học hình thang cân).

Xét DACD và DBDC có:

CD là cạnh chung;

AD = BC (chứng minh trên);

AC = BD (chứng minh trên).

Do ê DACD = DBDC (c.c.c)

Suy ra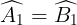 $\large \widehat{A_{1}}=\widehat{B_{1}}$ (hai góc tương ứng)

Lại có 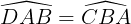$\large \widehat{DAB}=\widehat{CBA}$ (chứng minh trên)

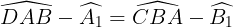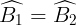
Nên $\large \widehat{DAB}-\widehat{A_{1}}=\widehat{CBA}-\widehat{B_{1}}$ ( $\large \widehat{B_{1}}=\widehat{B_{2}}$

Mặt không giống EG // AB nên 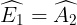$\large \widehat{E_{1}}=\widehat{A_{2}}$ (đồng vị) và 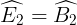$\large \widehat{E_{2}}=\widehat{B_{2}}$ (so le trong).

Suy đi ra 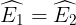$\large \widehat{E_{1}}=\widehat{E_{2}}$ , vì thế EG là tia phân giác của góc CEB.

Bài 7 trang 72 SGK toán 8/1 chân mây sáng sủa tạo

Áp dụng quyết định lí Pythagore vô DADE vuông bên trên E, tao có:

AD² = AE² + DE²

Suy đi ra DE² = AD² – AE² = 61² – 60² = 3 721 – 3 600 = 121 = 11²

Do ê DE = 11 centimet.

Kẻ BF ⊥ CD, khi ê BF là lối cao của hình thang cân nặng ABCD nên BF = 60 centimet.

Xét DADE và DBCF có:

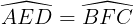$\large \widehat{AED}=\widehat{BFC}$ =90°;

AD = BC (do ABCD là hình thang cân);

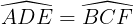$\large \widehat{ADE}=\widehat{BCF}$ (do ABCD là hình thang cân).

Do ê DADE = DBCF (cạnh huyền – góc nhọn)

Suy đi ra DE = CF = 11 centimet (hai cạnh tương ứng).

Mà DE + EF + CF = DC

Nên EF = DC – DE – CF = 92 – 11 – 11 = 70 centimet.

Tương tự động Vận dụng 4, trang 71, Sách giáo khoa Toán 8, tập luyện một, tao đơn giản dễ dàng minh chứng được AB = EF = 70 centimet.

Vậy chừng nhiều năm lòng nhỏ của hình thang cân nặng là 70 centimet.

4.3 Bài tập luyện hình thang cân nặng sách toán 8 cánh diều

Bài 1 trang 103 SGK toán 8/1 cánh diều

a) Do ABCD là hình thang cân nặng nên AC = BD và AD = BC (tính hóa học hình thang cân).

Xét ΔADC và ΔBCD có:

AD = BC; AC = BD; DC là cạnh chung

Do ê ΔADC = ΔBCD (c.c.c)

Suy ra 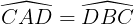$\large \widehat{CAD}=\widehat{DBC}$ (hai góc tương ứng)

Hay 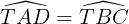$\large \widehat{TAD}=\widehat{TBC}$ .

Chứng minh tương tự động tao cũng có: ΔABD = ΔBAC (c.c.c)

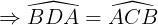$\large \Rightarrow \widehat{BDA}=\widehat{ACB}$ (hai góc tương ứng)

Hay 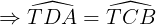$\large \Rightarrow \widehat{TDA}=\widehat{TCB}$ .

b) Xét ΔTAD và ΔTBC có:

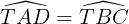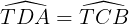$\large \widehat{TAD}=\widehat{TBC}$ ; AD = BC; $\large \widehat{TDA}=\widehat{TCB}$ .

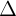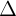Do ê $\large \Delta$ TAD = $\large \Delta$ TBC (g.c.g).

Suy đi ra TA = IB và TD = TC (các cặp cạnh tương ứng).

c) • Do TA = TB nên tam giác TAB cân nặng bên trên T.

ΔTAB cân nặng bên trên T với TM vừa phải là lối trung tuyến vừa phải là lối cao vì thế TM là lối trung trực của đoạn trực tiếp AB nên TM ⊥ AB.

• Do TD = TC nên tam giác TCD cân nặng bên trên T.

ΔTCD cân nặng bên trên T với TN vừa phải là lối trung tuyến vừa phải là lối cao vì thế TN là lối trung trực của đoạn trực tiếp CD nên TN ⊥ CD.

• Do AB // CD, TM ⊥ AB, TN ⊥ CD nên T, M, N trực tiếp hàng

Hay MN là lối trung trực của tất cả nhị đoạn trực tiếp AB và CD.

Bài 2 trang 104 SGK toán 8/1 cánh diều

Lời giải:

a) Do Δ ABE, Δ BED, Δ BDC là những tam giác đều nên

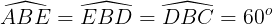
$\large \widehat{ABE}=\widehat{EBD}=\widehat{DBC}=60^{o}$
Do ê, $\large \widehat{ABC}=\widehat{ABE}+\widehat{EBD}+\widehat{DBC}=60^{o} + 60^{o}+60^{o}=180^{o}$

=> 3 điểm A, B, C trực tiếp mặt hàng.

b) Do Δ ABE, Δ BED là những tam giác đều nên 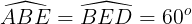$\large \widehat{ABE}=\widehat{BED}=60^{o}$

Mà nhị góc này ở địa điểm sánh le vô nên AC // ED

Tứ giác ACDE với AC // ED nên là hình thang.

Mặt không giống, 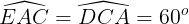$\large \widehat{EAC}=\widehat{DCA}=60^{o}$ (do Δ ABE, Δ BDC là những tam giác đều)

Do ê hình thang ACDE là hình thang cân nặng.

c) Vẽ lối cao EH của tam giác AEB.

Do AEB là tam giác đều nên H là trung điểm của AB

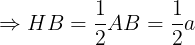
$\large \Rightarrow HB=\frac{1}{2}AB=\frac{1}{2}a$

Xét Δ EHB vuông bên trên H, theo gót quyết định lí Pythagore tao có:

EB² = EH² + HB²

Do ê EH² = EB² – HB²

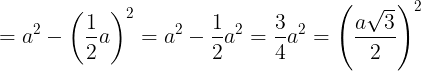
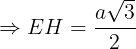
Ta với AC = AB + BC = a + a = 2a.

Diện tích hình thang cân nặng ACDE là:

$\large S=\frac{1}{2}(ED+AC).EH=\frac{1}{2}.(a+2a).\frac{a\sqrt{3}}{2}$

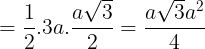
$\large =\frac{1}{2}.3a.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}a^{2}}{4}$

Bài 3 trang 104 SGK toán 8/1 cánh diều

Do ABCD là hình chữ nhật nên AD = BC, 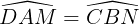$\large \widehat{DAM}=\widehat{CBN}$ = 90° và AB // CD.

Xét Δ AMD và Δ BNC có:

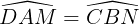$\large \widehat{DAM}=\widehat{CBN}$ = 90° (chứng minh trên);

AD = BC (chứng minh trên);

AM = BN (giả thiết).

Do ê Δ AMD = Δ BNC (hai cạnh góc vuông).

Suy ra 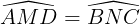$\large \widehat{AMD}=\widehat{BNC}$ (hai góc tương ứng).

Mặt không giống $\large \widehat{AMD}+\widehat{DMN}$ = 180°, $\large \widehat{BNC}+\widehat{CNM}$ = 180°(kề bù).

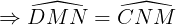
$\large \Rightarrow \widehat{DMN}=\widehat{CNM}$

Tứ giác MNCD với MN // CD (do AB // CD) nên là hình thang.

Lại có 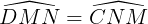$\large \widehat{DMN}=\widehat{CNM}$

=> hình thang MNCD là hình thang cân nặng.

Bài 4 trang 104 SGK toán 8/1 cánh diều

• Do ABC là tam giác cân nặng bên trên A nên 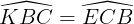$\large \widehat{KBC}=\widehat{ECB}$ .

Do BE và CK là những lối phân giác của ΔABC

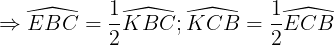
$\large \Rightarrow \widehat{EBC}=\frac{1}{2}\widehat{KBC};\widehat{KCB}=\frac{1}{2}\widehat{ECB}$

Do ê 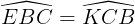$\large \widehat{EBC}=\widehat{KCB}$ .

• Xét ΔKBC và ΔECB có:

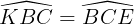$\large \widehat{KBC}=\widehat{BCE}$ ; BC là cạnh chung;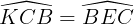 $\large \widehat{KCB}=\widehat{BEC}$

Do ê ΔKBC = ΔECB (g.c.g)

Suy đi ra BK = CE và CK = BE (các cặp cạnh tương ứng).

• Xét ΔBKE và ΔCEK có:

KE là cạnh chung; BK = CE; BE = CK

Do ê ΔBKE = ΔCEK (c.c.c)

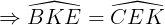$\large \Rightarrow \widehat{BKE}=\widehat{CEK}$ (hai góc tương ứng).

• Xét tứ giác BCEK có $\large \widehat{KBC}+\widehat{ECB}+\widehat{BKE}+\widehat{CEK}=360^{o}$ .

Hay $\large \widehat{KBC}+\widehat{KBC}+\widehat{BKE}+\widehat{BKE}=360^{o}$

Do đó $\large 2(\widehat{KBC}+\widehat{BKE})=360^{o}$ .

$\large \Rightarrow \widehat{KBC}+\widehat{BKE}=180^{o}$

Mặt khác $\large \widehat{AKE}+\widehat{BKE}=180^{o}$ (kề bù)

Do đó 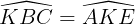$\large \widehat{KBC}=\widehat{AKE}$

Mà nhị góc này ở địa điểm đồng vị nên KE // BC

• Tứ giác BCEK với KE // BC nên là hình thang

Lại có 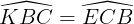$\large \widehat{KBC}=\widehat{ECB}$ nên hình thang BCEK là hình thang cân nặng.

Bài 5 trang 104 SGK toán 8/1 cánh diều

a) • Do BD // AE nên 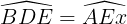$\large \widehat{BDE}=\widehat{AEx}$ = 60° (đồng vị)

Do AC // ED nên 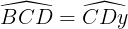$\large \widehat{BCD}=\widehat{CDy}$ = 60° và 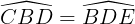$\large \widehat{CBD}=\widehat{BDE}$ = 60° (các cặp góc sánh le trong).

Ta có $\large \widehat{EBD}+\widehat{BDC}+\widehat{CDy}$ = 180°

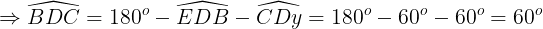
$\large \Rightarrow \widehat{BDC}= 180^{o}-\widehat{EDB}-\widehat{CDy}=180^{o}-60^{o}-60^{o}=60^{o}$

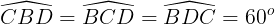Δ BCD với $\large \widehat{CBD}=\widehat{BCD}=\widehat{BDC}=60^{o}$ nên là tam giác đều.

=> BD = BC = CD = 2 m.

• ΔBDE với BD = DE = 2 m nên là tam giác cân nặng bên trên D

Lại có 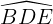$\large \widehat{BDE}$ = 60° nên Δ BDE là tam giác đều.

Suy đi ra BE = BD = DE = 2m và 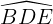$\large \widehat{BDE}$ = 60°.

• Do AC // ED nên 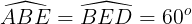$\large \widehat{ABE}=\widehat{BED}=60^{o}$ (so le trong).

Δ ABE với AE = BE = 2 m nên là tam giác cân nặng bên trên E.

Lại có 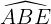$\large \widehat{ABE}$ = 60^o nên Δ ABE là tam giác đều.

b) • Do ΔBCD là tam giác đều nên lối cao BH đôi khi là lối trung tuyến của tam giác

Do ê H là trung điểm của BC

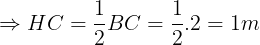
$\large \Rightarrow HC=\frac{1}{2}BC=\frac{1}{2}.2=1m$

Xét Δ DHC vuông bên trên H, theo gót quyết định lí Pythagore có:

CD² = HC² + DH²

Suy đi ra DH² = CD² – HC² = 2² – 1² = 3.

Do ê DH = 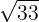$\large \sqrt{33}$ (m).

• Do ΔABE là tam giác đều nên AB = AE = 2 m.

Khi ê AC = AB + BC = 2 + 2 = 4 (m).

c) Diện tích mặt phẳng cắt đứng phần chứa chấp nước của con cái mương ê khi chan chứa nước là:

Xem thêm: Thành lập công ty tiếng Anh là gì? Thuật ngữ tiếng Anh về đăng ký doanh nghiệp

$\large S_{AEDC}=\frac{1}{2}(ED+AC).DH=\frac{1}{2}(2+4).\sqrt{3}=3\sqrt{3}m^{2}$

Trên đấy là những kiến thức và kỹ năng về hình thang cân lớp 8 vô công tác toán 8 liên kết trí thức, chân mây phát minh và cánh diều. Ngoài ra VUIHOC chỉ dẫn những em cơ hội giải những bài bác tập luyện vô sách giáo khoa. Truy cập cuongthinhcorp.com.vn nhằm update thêm thắt nhiều kiến thức và kỹ năng toán 8 có lợi nhé những em!

>> Mời chúng ta tìm hiểu thêm thêm: