Công thức tính diện tích bề mặt của hình cầu và ví dụ minh họa

Hình cầu là hình học tập thông thường gặp gỡ, không chỉ là vô toán học tập mà còn phải xuất hiện nay thật nhiều vô cuộc sống thường ngày. Hiểu rõ rệt về hình cầu, công thức tính diện tích S mặt phẳng, bạn cũng có thể giải quyết và xử lý đơn giản dễ dàng nhiều vấn đề tương quan. Hãy nằm trong mày mò về hình cầu, công thức tính diện tích S mặt phẳng và ví dụ minh họa.

Bạn đang xem: Công thức tính diện tích bề mặt của hình cầu và ví dụ minh họa

I. Hình cầu và diện tích S bề mặt

Hình cầu là 1 hình thể tròn xoe phụ thân chiều, từng điểm bên trên mặt phẳng đều phải có khoảng cách cho tới tâm cân nhau. Được tạo thành kể từ tâm O và nửa đường kính R. Quay nửa vòng xung quanh 2 lần bán kính cố định và thắt chặt, các bạn sẽ với cùng 1 hình cầu.

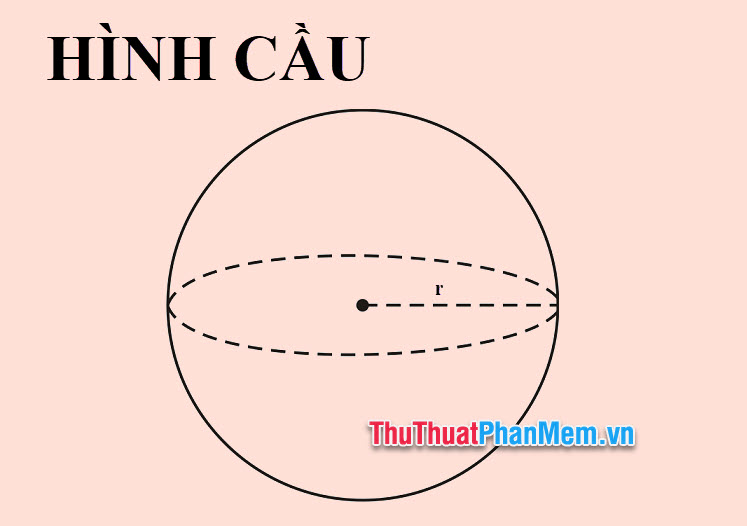
Bán kính của hình cầu là khoảng cách kể từ tâm cho tới mặt phẳng, diện tích S mặt phẳng của hình cầu là tổng diện tích S của toàn bộ những phần của chính nó. Theo khái niệm, diện tích S mặt mày của hình cầu được xem vì chưng 4 lượt diện tích S hình tròn trụ rộng lớn, hoặc vì chưng 4 lượt hằng số Pi nhân với bình phương nửa đường kính.

II. Công thức tính diện tích bề mặt hình cầu

Công thức tính diện tích bề mặt hình cầu: S=4πr2=πd2$S=4\pi r^2=\pi d^2$

Trong đó:

• S là diện tích S mặt phẳng của một trái ngược cầu
• π$\pi$ (số pi) là 1 hằng số với độ quý hiếm xấp xỉ 3.14159
• r$r$ là nửa đường kính của trái ngược cầu (khoảng cơ hội kể từ trung tâm của trái ngược cầu cho tới ngẫu nhiên điểm này bên trên mặt phẳng của trái ngược cầu)

Đối với 50% trái ngược cầu, diện tích S mặt phẳng của chính nó là tổng của 50% diện tích S mặt phẳng của trái ngược cầu cùng theo với diện tích S của lòng nửa trái ngược cầu (đó là 1 hình tròn).

S bề mặt bề cầu =12S bề mặt hình cầu +Sđáy =12(4πr2)+πr2$S_{\text{ bề mặt mày nửa cầu }}=\frac{1}{2}{S}_{\text{ bề mặt mày trái ngược cầu }}+S_{\text{đáy nửa cầu }}=\frac{1}{2}\left(4\pi r^2\right)+\pi r^2$

III. Các bài xích thói quen diện tích S mặt phẳng của trái ngược cầu

1. Tính diện tích S mặt phẳng của hình cầu Khi với vấn đề về buôn bán kính

Dạng bài xích này tiếp tục cung ứng nửa đường kính của hình cầu và đòi hỏi các bạn tính diện tích S mặt phẳng của chính nó.

Cách giải: Chỉ cần dùng công thức diện tích S mặt phẳng của hình cầu S=4πr2$S=4\pi r^2$ với r là nửa đường kính được thể hiện vô đề bài xích.

2. Tính diện tích S mặt phẳng của hình cầu lúc biết đàng kính

Dạng bài xích này đòi hỏi tính diện tích S mặt phẳng của hình cầu dựa vào vấn đề 2 lần bán kính được cung ứng.

Cách giải: Đơn giản tính nửa đường kính của hình cầu vì chưng 50% 2 lần bán kính, tiếp sau đó dùng công thức diện tích S mặt phẳng của hình cầu.

Hoặc bạn cũng có thể vận dụng công thức tính nửa đường kính của hình cầu theo đòi 2 lần bán kính S=πd2$S=\pi d^2$

3. Tính diện tích S mặt phẳng của hình cầu Khi với vấn đề về thể tích

Bài toán này đòi hỏi tính diện tích S mặt phẳng của hình cầu dựa vào vấn đề về thể tích.

Cách giải: Sử dụng công thức tính thể tích hình cầu nhằm lần rời khỏi nửa đường kính của hình cầu.

V=4πr33=>r3=3√3V4π$V=\frac{4\pi r^3}{3}=>r^3=\frac{3V}{4\pi }=>r=\sqrt[3]{\frac{3V}{4\pi }}$

Sau Khi tiếp tục biết nửa đường kính của hình cầu, dùng công thức tính diện tích S mặt phẳng của hình cầu nhằm tính diện tích S.

Xem thêm: Cách cảm ơn và phản hồi trong tiếng Anh - Moon ESL

IV. Ví dụ minh họa

Ví dụ 1: Cho một hình cầu, nửa đường kính nối kể từ tâm O nhiều năm 6cm. Hỏi diện tích S mặt phẳng của hình cầu là từng nào.

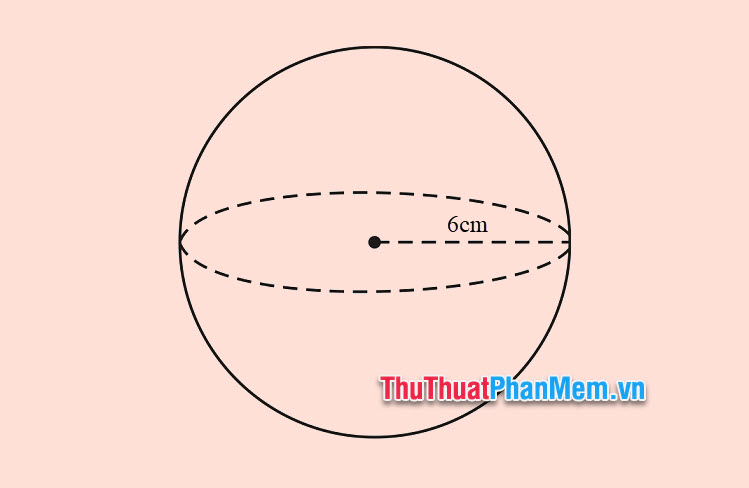
Bài giải

Bán kính hình cầu r = 6 centimet, dùng công thức diện tích S mặt phẳng của hình cầu S=4πr2$S=4\pi r^2$

S=4πr2$S=4\pi r^2=4\times \pi \times 6^2=144\times \pi =452.389{cm}^2$

Vậy diện tích bề mặt hình cầu là 452.389 cm2$452.389{cm}^2$.

Ví dụ 2: Cho hình cầu với 2 lần bán kính 10 centimet. Tính diện tích bề mặt hình cầu.

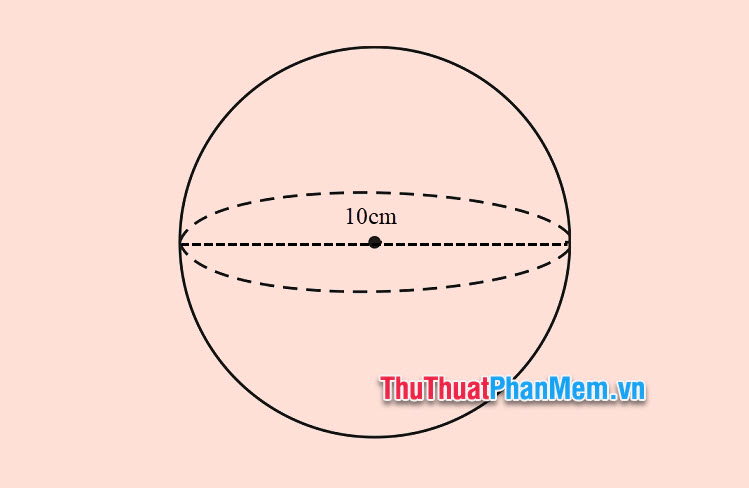
Bài giải

Áp dụng công thức tính diện tích bề mặt hình cầu theo đòi 2 lần bán kính S=πd2$S=\pi d^2$,

Ta có: S=πd2=π×102=314.159 cm2$S=\pi d^2=\pi \times {10}^2=314.159{cm}^2$

Vậy diện tích bề mặt hình cầu là 314.159 cm2$314.159{cm}^2$

Ví dụ 3: Cho một hình cầu rất có thể tích là V = 900 centimet khối. Tính diện tích bề mặt hình cầu.

Giải pháp

Áp dụng công thức tính nửa đường kính hình cầu, tao thu được:

r=3√3V4π=3√3×9004π≈6,345 cm$r=\sqrt[3]{\frac{3V}{4\pi }}=\sqrt[3]{\frac{3\times 900}{4\pi }\approx 6,345}cm$ cm

Công thức tính diện tích bề mặt hình cầu: S=4πr2=4π×6,3452=505,909 cm2$S=4\pi r^2=4\pi \times 6,{345}^2=505,909{cm}^2$

Xem thêm: 100+ hình nền Desktop, máy tính 4K Full HD đẹp nhất thế giới

Vậy diện tích bề mặt hình cầu là 505,909 cm2$505,909{cm}^2$

Do ê, Mytour tiếp tục share với các bạn kỹ năng về hình cầu, bao hàm công thức tính diện tích bề mặt hình cầu, cùng theo với những dạng bài xích tập dượt và ví dụ minh họa cụ thể. Hy vọng rằng với vấn đề này, các bạn sẽ làm rõ rộng lớn về phong thái tính diện tích bề mặt hình cầu và được thêm kỹ năng nhằm giải quyết và xử lý những bài xích tập dượt thực hành thực tế. Cảm ơn các bạn tiếp tục theo đòi dõi và quan hoài cho tới nội dung bài viết của công ty chúng tôi.