Đối với phần Hình học tập, Tam giác là 1 hình tuy rằng giản dị và đơn giản tuy nhiên nhiều các bạn vẫn còn đấy mơ hồ nước và ko tóm được kiến thức và kỹ năng cơ bạn dạng. Để chung học viên làm rõ rộng lớn về nội dung này, Gia Sư Việt tiếp tục đem về bài học kinh nghiệm về khái niệm, tấp tểnh lý, đặc điểm và cơ hội chứng tỏ những đàng Đồng quy nhập Tam giác. Chắc chắn phía trên được xem là biện pháp tương hỗ khá hiệu suất cao cho những em học viên nhập quy trình thực hiện bài xích luyện và kì thi đua cần thiết.
I. Đường phân giác
1. Tính hóa học của đàng phân giác
Tính hóa học 1: Điểm phía trên tia phân giác của một góc thì cơ hội đều nhị cạnh của góc đó
Bạn đang xem: Tổng hợp kiến thức về các đường Đồng quy trong Tam giác
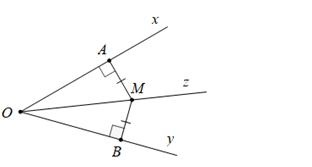
Từ hình vẽ, tao thấy:
M ∈ Oz
MA ⊥ Oy; MB ⊥ Oy
Dẫn đến: MA = MB, vì thế nhị tam giác vuông MOA = MOB
Tính hóa học 2: Điểm nằm cạnh nhập một góc và cơ hội đều nhị cạnh của góc thì phía trên tia phân giác của góc cơ.
Theo hình trên: Nếu M nằm nhập góc xOy và MA = MB thì M phía trên tia phân giác Oz của góc xOy
2. Định lý về đàng phân giác nhập Tam giác
Định lí 1: Ba đàng phân giác của một Tam giác đồng quy bên trên một điểm. Điểm này cơ hội đều phụ vương cạnh của Tam giác cơ.
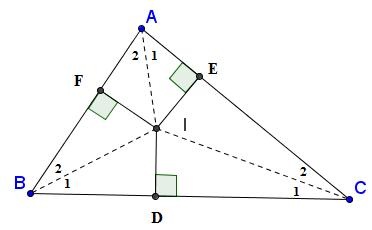
Từ hình vẽ, tao thấy: Tam giác ABC đem 3 đàng phân giác uỷ thác bên trên I. Khi đó:
Góc A1 = A2; Góc B1 = B2; Góc C1 = C2
Và ID = IE = IF
Định lí 2: Đường phân giác nhập của một Tam giác phân tách cạnh đối lập trở thành nhị đoạn trực tiếp tỷ trọng với nhị cạnh kề với đoạn ấy.
*Lưu ý: Vấn đề này cũng giống với đàng phân giác ngoài.
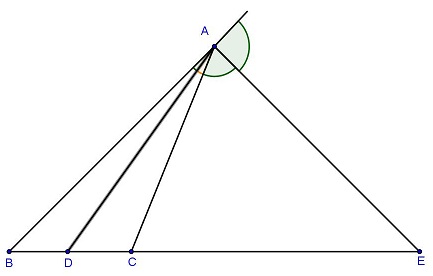
Từ hình vẽ, tao thấy:
DB/DC = AB/AC
EB/EC = AB/AC
*Chứng minh:
Qua đỉnh B vẽ đường thẳng liền mạch tuy vậy song với AC, tách đường thẳng liền mạch AD bên trên điểm E
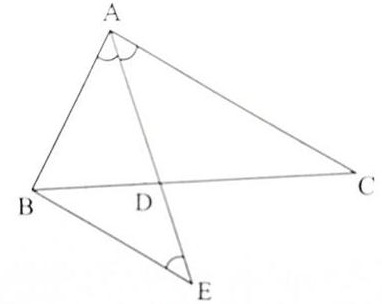
Ta có:
Góc BAE = Góc CAE (giả thuyết)
Vì BE // AC, nên Góc BEA = Góc CAE (so le trong)
Suy rời khỏi Góc BAE = Góc BEA . Do cơ tam giác ABE cân nặng bên trên B, suy ra:
BE = AB (1)
Áp dụng hệ trái ngược của tấp tểnh lí Ta-let so với tam giác DAC, tao có:
DB/DC = BE/AC (2)
Từ (1) và (2) suy ra: DB/DC = AB/AC
Như vậy, chân những đàng phân giác nhập và phân giác ngoài của một góc bên trên một đỉnh của tam giác là những điểm phân tách nhập và phân tách ngoài các cạnh đối lập bám theo tỉ số vày tỉ số của nhị cạnh mặt mũi tương ứng: DB/DC = EB/EC = AB/AC
3. Cách chứng tỏ đàng phân giác
– Cách 1: Chứng minh nhị góc ở một đỉnh cân nhau.
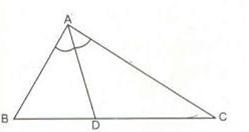
Ví dụ: Tam giác ABC đem AD phân tách góc A trở thành nhị góc BAD và góc CAD cân nhau. => AD là đàng phân giác bên trên đỉnh A của tam giác ABC
– Cách 2: Chứng minh nhị đoạn trực tiếp đối lập tỷ trọng với nhị cạnh kề với đoạn ấy.
Ví dụ: Tam giác ABC đem DB/DC = AB/AC
=> AD là đàng phân giác bên trên đỉnh A của tam giác ABC
– Cách 3 (Dùng nhập tình huống tam giác cân): Chứng minh đàng này là đàng trung tuyến nhập tam giác cân nặng.
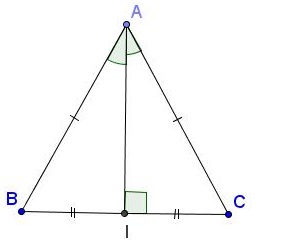
Ví dụ: Tam giác ABC cân nặng đem AD là đàng trung tuyến => AD cũng mặt khác là đàng phân giác bên trên đỉnh A của tam giác ABC
II. Đường trung trực
Định nghĩa: Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch vuông góc với đoạn trực tiếp ấy bên trên trung điểm của chính nó.
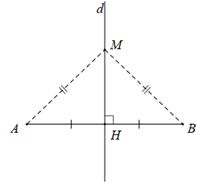
1. Tính hóa học đàng trung trực
Tính hóa học 1: Điểm phía trên đàng trung trực của một quãng trực tiếp thì cơ hội đều nhị mút của đoạn trực tiếp cơ.
Ví dụ: M nằm trong đàng trung trực của AB => MA = MB
Tính hóa học 2: Điểm cơ hội đều nhị mút của đoạn trực tiếp thì phía trên đàng trung trực của đoạn trực tiếp cơ.
Ví dụ: MA = MB => M nằm trong đàng trung trực của AB
2. Định lý đàng trung trực nhập Tam giác
Định lí 1: Ba đàng trung trực của một tam giác nằm trong trải qua một điểm. Điểm này cơ hội đều phụ vương đỉnh của tam giác cơ.
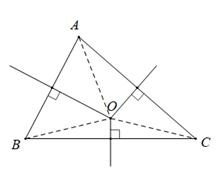
Từ hình vẽ, tao thấy:
Điểm O là uỷ thác điểm những đàng trung trực trong ∆ABC
OA = OB = OC
=> O là tâm đàng tròn xoe nước ngoài tiếp ∆ABC
Định lí 2: Trong một tam giác cân nặng, đàng trung trực của cạnh lòng mặt khác là đàng trung tuyến ứng với cạnh này.
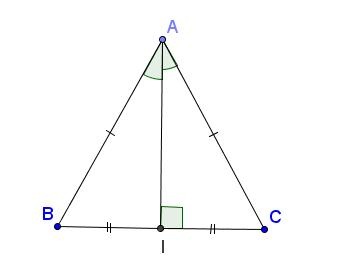
Ví dụ: ∆ABC đem AD là đàng trung tuyến của đáy
=> AD cũng mặt khác là đàng trung trực bên trên đỉnh A của tam giác ABC
3. Cách chứng tỏ đàng trung trực
– Cách 1: Chứng minh đàng cơ vuông góc với 1 cạnh của tam giác bên trên trung điểm.
Ví dụ: Tam giác ABC đem AD ⊥ BC bên trên trung điểm của BC
=> AD là đàng trung trực ứng với BC của tam giác ABC
– Cách 2: Chứng minh mang trong mình 1 điểm cơ hội phía trên đàng cơ cơ hội đều 2 cạnh mặt mũi.
Ví dụ: Tam giác ABC đem điểm M ∈ AD, MA = MB
=> AD là đàng trung trực bên trên đỉnh A của tam giác ABC
– Cách 3 (Dùng nhập tình huống tam giác cân): Chứng minh đàng này là đàng trung tuyến nhập tam giác cân
Xem thêm: bạn cứ yên tâm Tiếng Anh là gì
Ví dụ: Tam giác ABC cân nặng đem AD là đàng trung tuyến
=> AD cũng mặt khác là đàng trung trực ứng với lòng của tam giác ABC
III. Đường trung tuyến
Định nghĩa: Đường trung tuyến của một tam giác là 1 đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
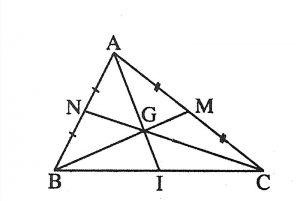
1. Định lý về đàng trung tuyến nhập Tam giác
Định lý 1: Ba đàng trung tuyến của một tam giác nằm trong đồng quy bên trên một điểm, điểm đó được gọi là trọng tâm của tam giác.
Định lý 2: Khoảng cơ hội kể từ trọng tâm cho tới từng đỉnh của tam giác vày ⅔ đàng trung tuyến ứng với đỉnh cơ.
Định lý 3: Khoảng cơ hội kể từ trọng tâm cho tới trung điểm của từng cạnh vày ⅓ đàng trung tuyến ứng với điểm cơ.
Ví dụ: Tam giác ABC đem G là trọng tâm
AG = 2/3 AI; BG = 2/3 BM; CG = 2/3 CN
GI = 1/3 AI; GM = 1/3 BM; GN = 1/3 CN
2. Tính hóa học về đàng trung tuyến
Tính chất 1: Trong tam giác cân nặng (hoặc tam giác đều) đàng trung tuyến ứng với cạnh lòng phân tách tam giác trở thành nhị tam giác cân nhau.
Ví dụ: Tam giác ABC cân nặng đem AD là đàng trung tuyến
=> Diện tích ABD = ACD
Tính hóa học 2: Trong tam giác vuông, đàng trung tuyến ứng với cạnh huyền vày ½ cạnh huyền.
Ví dụ: Tam giác ABC vuông bên trên A đem AM là đàng trung tuyến
=> AM = MB = MC = 50% BC
3. Cách chứng tỏ đàng trung tuyến
– Cách 1: Chứng minh đàng cơ nối một đỉnh của tam giác với trung điểm cạnh đối lập.
Ví dụ: Tam giác ABC đem D là trung điểm BC
=> AD là đàng trung tuyến của tam giác ABC
– Cách 2: Chứng minh khoảng cách kể từ trọng tâm cho tới từng đỉnh của tam giác vày ⅔ đàng trung tuyến ứng với đỉnh cơ.
Ví dụ: Tam giác ABC đem điểm G thỏa mãn nhu cầu AG = 2/3 AD (D ∈ BC)
=> AD là đàng trung tuyến của tam giác ABC
– Cách 3: Chứng minh khoảng cách kể từ trọng tâm cho tới trung điểm của từng cạnh vày ⅓ đàng trung tuyến ứng với điểm cơ.
Ví dụ: Tam giác ABC đem điểm G thỏa mãn nhu cầu GD = 1/3 AD (D ∈ BC)
=> AD là đàng trung tuyến của tam giác ABC
IV. Đường cao
1. Tính hóa học về đàng cao
Tính hóa học 1: Trong tam giác cân nặng, đàng cao ứng với cạnh lòng đó là đàng trung tuyến ứng với cạnh cơ, là đàng phân giác của góc ở đỉnh và đàng trung trực của lòng tam giác.
Ví dụ: Tam giác cân nặng ABC đem AI là đàng cao
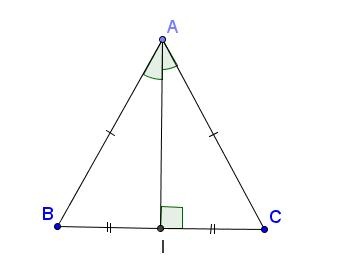
=> AI cũng chính là đàng trung tuyến ứng với BC, tia phân giác góc A và đàng trung trực của BC.
Tính hóa học 2: Trong tam giác vuông, đàng cao với lòng là 1 cạnh góc vuông đó là cạnh góc vuông sót lại. Như vậy thì đỉnh góc vuông đó là chân đàng cao hạ kể từ nhị đỉnh sót lại xuống nhị cạnh góc vuông của tam giác.
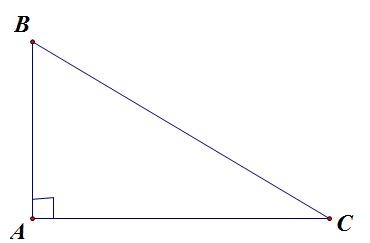
Ví dụ: Tam giác ABC vuông bên trên A
=> BA là đàng cao ứng với AC, CA là đàng cao ứng với AB
2. Định lý về đàng cao nhập Tam giác
Định lí 1: Ba đàng cao của một tam giác đồng quy bên trên một điểm. Điểm cơ gọi là trực tâm của tam giác.
Ví dụ: Cho hình vẽ sau. Chứng minh NS ⊥ ML
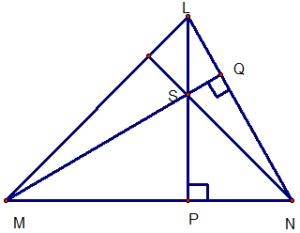
Xét ΔMNL, tao có:
LP MN (gt) => LP là đàng cao loại nhất.
MQ LN (gt) => MQ là đàng cao loại nhị.
LP tách MQ bên trên S.
=> S là trực tâm của ΔMNL
=> NS là đàng cao loại phụ vương.
=> NS ⊥ ML
Định lí 2: Trong tam giác vuông, đàng cao ứng với cạnh lòng phân tách tam giác trở thành nhị tam giác đồng dạng.
Ví dụ: Tam giác ABC vuông bên trên A
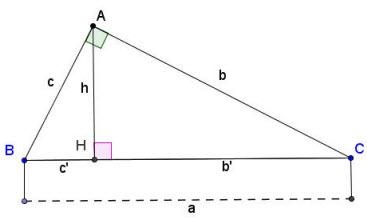
=> ΔABH ~ ΔACH
*Một số đẳng thức liên quan:
Đẳng thức mặt mũi trái: c2 = c’×a
Đẳng thức mặt mũi phải: b2 = b’×a
Đẳng thức ở giữa: h2 = b’×c’
3. Cách chứng tỏ đàng cao
– Cách 1: Chứng minh đàng cơ vuông góc với 1 cạnh của tam giác.
Ví dụ: Tam giác ABC đem AH ⊥ BC
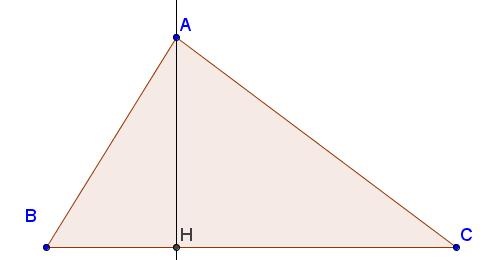
=> AH là đàng cao của tam giác ABC
– Cách 2: Dùng tấp tểnh lí Py-ta-go hoặc những đẳng thức nhập tam giác vuông
Ví dụ: Tam giác ABC đem H nằm trong BC, (BC)2 = (AB)2 + (AC)2
=> AH là đàng cao ứng với BC
Ví dụ: Tam giác ABC vuông bên trên A, đem (AH)2 = HB × HC
=> AH là đàng cao ứng với BC
Lời kết: Mong rằng bài học kinh nghiệm bên trên phía trên về những đàng đồng quy nhập Tam giác sẽ hỗ trợ chúng ta mang trong mình 1 tầm nhìn sâu sắc và nhiều chiều rộng lớn về hình học tập. Đồng thời cũng ghi lưu giữ những công thức và tấp tểnh lí quan trọng Khi giải bài xích luyện tương quan cho tới tam giác, Gia Sư Việt van lơn chúc chúng ta tiếp nhận và tiếp thu kiến thức hiệu suất cao nhất. Nếu các bạn cần gia sư Toán tương hỗ việc học tập tận nơi, vui sướng lòng contact công ty chúng tôi qua quýt số 096.446.0088 – 090.462.8800 nhằm hiểu biết thêm cụ thể.
Xem thêm: 70+ từ vựng về các phòng trong nhà bằng tiếng Anh
Tham khảo thêm:
♦ Định nghĩa, đặc điểm & cơ hội chứng tỏ những Tam giác đặc biệt
♦ Khái niệm, đặc điểm & cơ hội chứng tỏ Tứ giác là Hình bình hành














