Bảng tổng hợp công thức lượng giác đầy đủ

By Admin 28/03/2024 0

Bảng tổ hợp rất đầy đủ những công thức thức lượng giác trung học phổ thông được khối hệ thống khoa học tập, ngắn ngủi gọn gàng gom những em học viên rất có thể đơn giản dễ dàng học tập và vận dụng trong những dạng bài xích tương quan cho tới công thức lượng giác. Tham khảo ngay!

1. Khái niệm tỉ con số giác của góc nhọn

Bạn đang xem: Bảng tổng hợp công thức lượng giác đầy đủ

tỉ con số giác của góc nhọn

Xét tình huống nhập một tam giác vuông tớ sẽ sở hữu được công thức về tỉ con số giác như sau:

sin : được xem tà tà tỉ số thân mật phỏng nhiều năm cạnh đối và phỏng nhiều năm cạnh huyền của góc

cos : được xem là tỉ số thân mật phỏng nhiều năm cạnh kề và độ dài cạnh huyền của góc

tan : được xem là tỉ số giữa độ dài cạnh đối và độ dài cạnh kề của góc

cot : được xem là tỉ số giữa độ dài cạnh kề và cạnh đối của góc

Mẹo học tập nằm trong công thức lượng giác : "Sin đến lớp, Cos ko hỏng, Tan liên minh, ,Cot kết đoàn"

2. Các công thức lượng giác cơ bản:

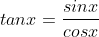
tanx= \frac{sinx}{cosx}

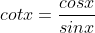
cotx= \frac{cosx}{sinx}

sin^{2}x + cos^{2}x = 1

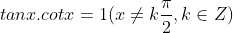
tanx . cotx = 1 (x\neq k\frac{\pi }{2}, k\in Z )

1 + tan^{2}x = \frac{1}{cos^{2}x} (x \neq \frac{\pi }{2}+k\pi , k\in Z)

1 + cot^{2}x = \frac{1}{sin^{2}x} (x \neq \frac{\pi }{2}+k\pi , k\in Z)

3. Các công thức nằm trong lượng giác

sin (a ± b) = sin a.cos b ± cos a.sin b

cos (a + b) = cos a.cos b - sin a.sin b

cos (a - b) = cos a.cos b + sin a.sin b

tan(a+b) = \frac{tan a + tan b}{1 - tan a.tan b}

tan(a-b) = \frac{tan a - tan b}{1 + tan a.tan b}

Mẹo học tập nằm trong công thức nằm trong lượng giác: 

Các em học viên rất có thể học tập công thức nằm trong lượng giác theo đòi câu thơ sau: "Sin thì sin cos cos sin, cos thì cos cos sin sin vệt trừ. Tan thì tan nọ tan tê liệt phân tách mang lại khuôn mẫu số 1 trừ tan tan."

4. Công thức những cung links bên trên đàng tròn trặn lượng giác

Trong tình huống 2 góc đối nhau

cos (-x) = cos x

sin (-x) = -sin x

tan (-x) = -tan x

cot (-x) = -cot x

Trong tình huống 2 góc bù nhau

sin (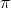\pi - x) = sin x

cos (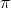\pi - x) = -cos x

tan (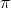\pi - x) = -tan x

cot (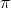\pi - x) = -cot x

Trong tình huống 2 góc phụ nhau

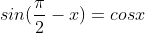
sin(\frac{\pi }{2} - x) = cosx

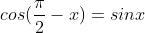
cos(\frac{\pi }{2} - x) = sinx

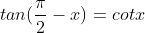
tan(\frac{\pi }{2} - x) = cotx

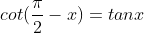
cot(\frac{\pi }{2} - x) = tanx

Trong tình huống nhị góc rộng lớn xoàng xĩnh π

sin (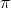\pi  + x) = -sin x

cos (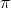\pi + x) = -cos x

tan (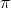\pi  + x) = tan x

cot (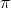\pi  + x) = cot x

Trong tình huống nhị góc rộng lớn xoàng xĩnh π/2:

sin(\frac{\pi }{2} + x) = cosx

cos(\frac{\pi }{2} + x) = -sinx

tan(\frac{\pi }{2} + x) = -cotx

cot(\frac{\pi }{2} + x) = -tanx

Nắm hoàn toàn kỹ năng và kiến thức và cách thức giải từng dạng bài xích luyện về phương trình lượng giác với cỗ tư liệu hiểu quyền của VUIHOC ngay

5. Công thức nhân lượng giác

Công thức lượng giác nhân đôi

sin2x = 2sinx.cosx

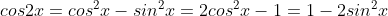
cos2x = cos^{2}x - sin^{2}x = 2cos^{2}x - 1 = 1 - 2sin^{2}x

tan2x = \frac{2tanx}{1 - tan^{2}x}

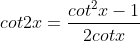
cot2x = \frac{cot^{2}x - 1}{2cotx}

Công thức lượng giác nhân ba

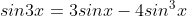
sin3x = 3sinx - 4sin^{3}x

cos3x = 4cos^{3}x - 3cosx

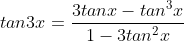
tan3x = \frac{3tanx - tan^{3}x}{1 - 3tan^{2}x}

Công thức lượng giác nhân bốn

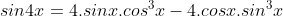
sin4x = 4.sinx.cos^{3}x - 4.cosx.sin^{3}x

cos4x = 8.cos^{4}x - 8.cos^{2}x + 1

hoặc tớ rất có thể sử dụng cos4x = 8.sin^{4}x - 8.sin^{2}x + 1

6. Công thức hạ bậc lượng giác

Về cơ bạn dạng công thức hạ bậc lượng giác đều được đổi khác kể từ công thức lượng giác cơ bản:

sin^{2}x = 1 - cos^{2}x = 1 - \frac{cos2x + 1}{2} = \frac{1 - cos2x}{2}

cos^{2}x = \frac{1 + cos2x}{2}

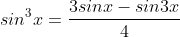
sin^{3}x = \frac{3sinx - sin3x}{4}

cos^{3}x = \frac{3cosx + cos3x}{4}

7. Công thức lượng giác vươn lên là tổng trở thành tích

cosa + cosb = 2cos\frac{a+b}{2}.cos\frac{a-b}{2}

cosa - cosb = -2sin\frac{a+b}{2}.sin\frac{a-b}{2}

sina + sinb = 2sin\frac{a+b}{2}.cos\frac{a-b}{2}

sina - sinb = 2cos\frac{a+b}{2}.sin\frac{a-b}{2}

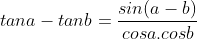
tana + tanb = \frac{sin(a+b)}{cosa.cosb}

tana - tanb = \frac{sin(a-b)}{cosa.cosb}

sina + cosa = \sqrt{2}sin(a + \frac{\pi }{4}) = \sqrt{2}cos(a - \frac{\pi }{4})

sina - cosa = \sqrt{2}sin(a - \frac{\pi }{4}) = -\sqrt{2}cos(a + \frac{\pi }{4})

tana + cota = \frac{2}{sin2a}

cota - tana = 2cot2a

sin^{4}a + cos^{4}a = 1 - \frac{1}{2}sin^{2}2a = \frac{1}{4}cos4a + \frac{3}{4}

sin^{6}a + cos^{6}a = 1 - \frac{3}{4}sin^{2}2a = \frac{3}{8}cos4a + \frac{5}{8}

8. Công thức lượng giác đổi khác tích trở thành tổng

cosa.cosb = \frac{1}{2}[cos(a+b) + cos(a-b)]

sina.sinb = -\frac{1}{2}[cos(a+b) - cos(a-b)]

sina.cosb = -\frac{1}{2}[sin(a+b) + sin(a-b)]

9. Công thức nghiệm của phương trình lượng giác

Đối với những phương trình lượng giác cơ bản

sina = sinb \Leftrightarrow \begin{bmatrix} a = b + k2\pi & \\ a = \pi - b + 2k\pi & k \in Z \end{bmatrix}

cosa = cosb \Leftrightarrow \begin{bmatrix} a = b + k2\pi & \\ a = - b + 2k\pi & k \in Z \end{bmatrix}

tana = tanb \Leftrightarrow a = b + k\pi ; k \in Z

cota = cotb \Leftrightarrow a = b + k\pi ; k \in Z

Phương trình lượng giác nhập tình huống quánh biệt

sina = 0 \Leftrightarrow a = k\pi (k\in Z)

Xem thêm: c%C3%A2y trong Tiếng Anh, dịch, Tiếng Việt

sina = 1 \Leftrightarrow a = \frac{\pi }{2} + 2k\pi (k\in Z)

sina = -1 \Leftrightarrow a = -\frac{\pi }{2} + 2k\pi (k\in Z)

cosa = 0 \Leftrightarrow a = \frac{\pi }{2} + k\pi (k\in Z)

cosa = 1 \Leftrightarrow a = 2k\pi (k\in Z)

cosa = -1 \Leftrightarrow a = \pi + 2k\pi (k\in Z)

Đăng ký tức thì và để được những thầy cô ôn luyện kỹ năng và kiến thức và kiến thiết trong suốt lộ trình ôn thi đua toán trung học phổ thông sớm tức thì kể từ bây giờ

10. Bảng xét vệt của những độ quý hiếm lượng giác

Góc phần tư số I II III IV
Sinx dương dương âm âm
Cosx dương âm âm dương
Tanx dương âm dương âm
Cotx dương âm dương âm

11. Bảng độ quý hiếm lượng giác của những góc quánh biệt

Tỉ con số giác của 2 góc phụ nhau (là 2 góc đem tổng vì như thế 90 độ)

sina = cosb.cosa = sinb

tana = cotb.cota = tanb

Bảng độ quý hiếm lượng giác của những góc quánh biệt

a

(0 độ)

\frac{\pi }{6}

(30 độ)

\frac{\pi }{4}

(45 độ)

\frac{\pi }{3}

(60 độ)

\frac{\pi }{2}

(90 độ)

\frac{2\pi }{3}

(120 độ)

\frac{3\pi }{4}

(135 độ)

\frac{5\pi }{6}

(150 độ)

\pi

(180 độ)

\frac{3\pi }{2}

(270 độ)

2\pi

(360 độ)
sina 0 \frac{1}{2} \frac{\sqrt{2}}{2} \frac{\sqrt{3}}{2} 1 \frac{\sqrt{3}}{2} \frac{\sqrt{2}}{2} \frac{1}{2} 0 -1 0
cosa 1 \frac{\sqrt{3}}{2} \frac{\sqrt{2}}{2} \frac{1}{2} 0 \frac{-1}{2} \frac{-\sqrt{2}}{2} \frac{-\sqrt{3}}{2} -1 0 -1
tana 0 \frac{1}{\sqrt{3}} 1 \sqrt{3} \parallel -\sqrt{3} -1 -\frac{1}{\sqrt{3}} 0 \parallel 0
cota \parallel \sqrt{3} 1 \frac{1}{\sqrt{3}} 0 -\frac{1}{\sqrt{3}} -1 -\sqrt{3} \parallel 0 \parallel

12. Các công thức lượng giác nâng lên vấp ngã sung

Đặt 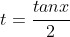 t = \frac{tanx}{2}

Lúc này tớ rất có thể trình diễn những công thức lượng giác không giống theo đòi t như sau:

sinx = \frac{2t}{1 + t^{2}}

cosx = \frac{1 - t^{2}}{1 + t^{2}}

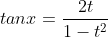
tanx = \frac{2t}{1 - t^{2}}

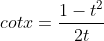
cotx = \frac{1 - t^{2}}{2t}

13. Các bài xích thơ về công thức lượng giác

Bài thơ về công thức nằm trong lượng giác

"Sin thì sin cos cos sin 

Cos thì cos cos sin sin rồi trừ

Tang tổng thì lấy tổng tang

Chia 1 trừ với tích tang, dễ dàng tuy nhiên."

Bài thơ về công thức về tan tổng

  tan(a+b) = \frac{tan a + tan b}{1 - tan a.tan b}

"Tan 2 tổng 2 tầng phía trên cao rộng

Trên thượng tằng tan nằm trong và tan

Hạ tầng số 1 đặc biệt ngang tàng

Dám trừ cút cả tan tan anh hùng"

Câu thơ ghi lưu giữ báo giá trị lượng giác của những cung tương quan quánh biệt

"Cos đối, sin bù, phụ chéo cánh, tan rộng lớn xoàng xĩnh pi (π)"

Câu thơ ghi lưu giữ nhanh chóng công thức lượng giác đổi khác tổng trở thành tích

"Tính sin tổng tớ lập tổng sin cô

Tính cô tổng lập tớ hiệu song cô song chàng

Còn tính tan tử + song tan (hay là: tan tổng lập tổng 2 tan)

1 trừ tan tích khuôn mẫu đem thương rầu

Nếu gặp gỡ hiệu tớ chớ lo lắng,

Đổi trừ trở thành nằm trong ghi sâu sắc nhập lòng"

Đặc biệt so với tình huống tổng của tan tớ có:

"Tang bản thân + với tang tớ, vì như thế sin 2 đứa bên trên cos tớ cos mình"

tana + tanb: "Tình bản thân nằm trong lại tình tớ, sinh đi ra nhị người con bản thân con cái ta"

tana – tanb: "Tình bản thân trừ với tình tớ sinh đi ra hiệu bọn chúng, con cái tớ con cái mình"

Câu thơ ghi lưu giữ nhanh chóng công thức lượng giác nhân đôi

sin2a= 2sina.cosa (tương tự động với những công thức khác)

Phương pháp lưu giữ nhanh:

"Sin gấp hai vì như thế 2 sin cos

Cos gấp hai vì như thế bình phương cos trừ cút bình sin

Bằng trừ 1 nằm trong nhị bình cos

Bằng nằm trong 1 trừ nhị bình sin

(Chúng tớ chỉ việc lưu giữ những công thức nhân song của cos vì như thế câu lưu giữ bên trên rồi chính thức kể từ tê liệt rất có thể suy đi ra những công thức hạ bậc.)

Tan gấp hai vì như thế Tan song tớ lấy song tan (2 tan )

Chia một trừ lại bình tan, đi ra ngay lập tức."

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học tập online ĐẦU TIÊN VÀ DUY NHẤT:  

⭐ Xây dựng trong suốt lộ trình học tập kể từ thất lạc gốc cho tới 27+  

⭐ Chọn thầy cô, lớp, môn học tập theo đòi sở thích  

⭐ Tương tác thẳng hai phía nằm trong thầy cô  

⭐ Học đến lớp lại cho tới lúc nào hiểu bài xích thì thôi

⭐ Rèn tips tricks gom bức tốc thời hạn thực hiện đề

⭐ Tặng full cỗ tư liệu độc quyền nhập quy trình học tập tập

Đăng ký học tập test không tính phí ngay!!

Trên đấy là toàn cỗ những kỹ năng và kiến thức cần thiết tuy nhiên những em học viên cần thiết bắt được về Công thức lượng giác. Hy vọng với nội dung bài viết bên trên sẽ hỗ trợ những em đơn giản dễ dàng ghi lưu giữ công thức nhằm xử lý những bài xích luyện tương quan cho tới lượng giác cũng như gom những em khối hệ thống con kiến thức trong quy trình ôn thi đua Toán trung học phổ thông Quốc gia. Để dò thám hiểu tăng về kỹ năng và kiến thức về Toán 12 hay các môn học tập không giống, những em học viên rất có thể truy vấn thẳng nhập website: cuongthinhcorp.com.vn. Chúc những em đạt được sản phẩm tốt nhất có thể trong những kì thi đua tiếp đây.

Bài viết lách rất có thể xem thêm thêm:

Xét Tính Đơn Điệu Của Hàm Số Lượng Giác

Xem thêm: 20+ Cách Chào Hỏi Bằng Tiếng Anh Hay Nhất

Lý thuyết và những dạng bài xích luyện hàm con số giác

Các Dạng Phương Trình Lượng Giác

Nguyên dung lượng giác cơ bản