Công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3, 2a và một trong những dạng bài bác tập dượt tương quan nằm trong chỉ dẫn giải cụ thể nhất, tìm hiểu thêm bên trên phía trên.

Bạn đang xem: Công thức tính thể tích khối tứ diện đều cạnh a và bài tập

Bài viết lách này được đăng bên trên cuongthinhcorp.com.vn, ko được copy bên dưới từng mẫu mã.
Khối tứ diện đều là một trong phần kỹ năng rất rất cần thiết và thông thường xuyên xuất hiện tại trong những bài bác thi đua trung học phổ thông Quốc Gia. Trong số đó, thể tích khối tứ diện đều là một trong nội dung ko thể nào là bỏ lỡ được, hiểu rõ yếu tố này nhập nội dung bài viết thời điểm hôm nay, freetuts tiếp tục share cho tới cho những em những kỹ năng tương quan cho tới tính thể tích của khối tứ diện đều và một trong những bài bác tập dượt tương quan nhằm những em hoàn toàn có thể ôn luyện nội dung này thiệt đảm bảo chất lượng.
Khối tứ diện đều là gì?
Trong hình học tập không khí, khối tứ diện đều hoặc hay còn gọi là hình chóp tam giác đều là một trong khối nhiều diện sở hữu 4 mặt mày là 4 tam giác đều và sở hữu 2 đặc điểm cơ phiên bản sau.
- Tất cả những mặt mày của tứ diện đều là những tam giác đều phải sở hữu diện tích S đều nhau.
- Tất cả những cạnh của tứ diện đều thì có tính nhiều năm đều nhau.
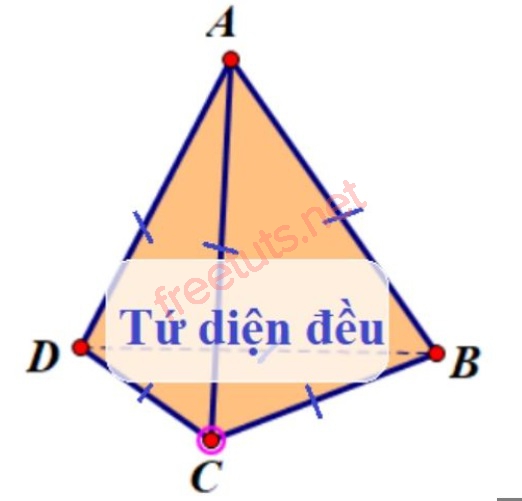
Ví dụ về khối tứ diện đều ABCD.
Công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3
Để tính thể tích của khối tứ diện đều phải sở hữu những cạnh là a, a, a√2, a√3, 2a, những em hãy tuân theo chỉ dẫn sau:
Bài viết lách này được đăng bên trên [free tuts .net]
Thể tích khối tứ diện đều cạnh a
Cho tứ diện đều ABCD, có tính nhiều năm những cạnh đều nhau và vì chưng a, tính thể tích khối tứ diện ABCD.
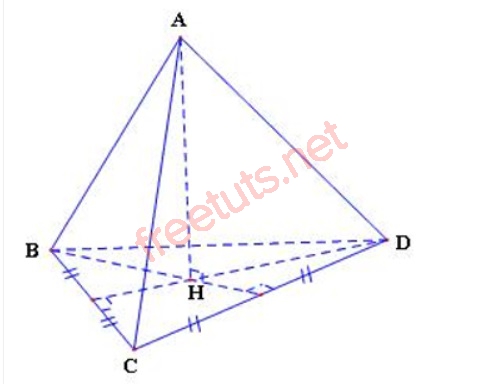
Hình hình ảnh minh họa tứ diện đều ABCD.
Lời giải:
Ta sở hữu diện tích S tam giác đều BCD cạnh a là:
S(BCD) = (a^2.a√3)/4
Gọi H là trọng tâm tam giác BCD nên AH vuông góc với (BCD)
Xét tam giác vuông ABH, có:
AH = √(AB^2 - BH^2) = (a√6)/3
Vậy thể tích của khối tứ diện đều cạnh a là:
V(ABCD) = 1/3 . S(BCD).AH = ⅓. (a^2√3)/4.(a√6)/3 = (a^3√2)/12
Công thức như sau:
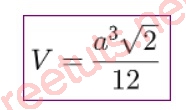
Thể tích khối tứ diện đều cạnh a√2
Với khối tứ diện đều phải sở hữu cạnh là a√2, thế a√2 nhập công thức bên trên tớ có:
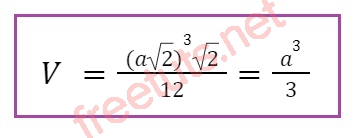
Thể tích khối tứ diện đều cạnh a√3
Với khối tứ diện đều phải sở hữu cạnh là a√3, thế a√3 nhập công thức bên trên tớ có:
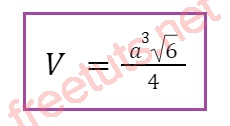
Thể tích khối tứ diện đều cạnh 2a
Với khối tứ diện đều phải sở hữu cạnh là 2a, thế 2a nhập công thức bên trên tớ có:

Lưu ý Lúc tinh ranh thể tích khối tứ diện đều
Muốn giải được những việc tính thể tích cùa một khối tứ diện đều, điều cần thiết tuy nhiên những em cần thiết Note này là kiểu vẽ tứ diện đều sao mang đến đúng đắn. Hãy tìm hiểu thêm công việc tuy nhiên freetuts tiếp tục liệt kê sau đây nha:
Xem thêm: "Phơi Quần Áo" trong Tiếng Anh là gì: Định Nghĩa, Ví Dụ Anh Việt
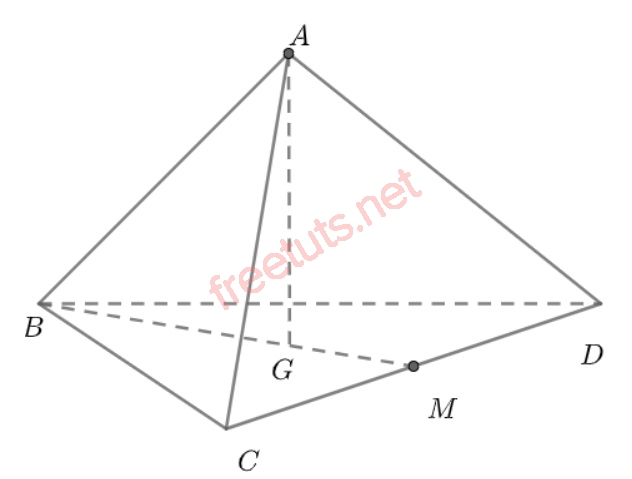
Cách vẽ hình tứ diện đều ABCD.
Coi hình tứ diện này là hình chóp tam giác đều. Vi dụ A.BCD
- Trong mặt mày lòng (BCD), vẽ lối trung tuyến BM, vậy BM là trung tuyến của tam giác BCD.
- Xác lăm le điểm trọng tâm G của tam giác BCD, và G cũng đó là tâm của lòng.
- Dựng lối cao trải qua G tuy nhiên song với mép vở.
- Trên lối cao một vừa hai phải dựng, xác lập điểm A, nối A với 3 điểm B, C, D là tất cả chúng ta tiếp tục đầy đủ được hình chóp đều ABCD.
Bài thói quen thể tích khối tứ diện đều
Bài 1: Cho tứ diện ABCD, sở hữu ABC, ABD là 2 tam giác đều cạnh a, ACD vuông góc với BCD.
a. Tính thể tích khối tứ diện ABCD theo đòi a.
b. Tính so đọ góc thân thích 2 đường thẳng liền mạch AD và BC
Lời giải:
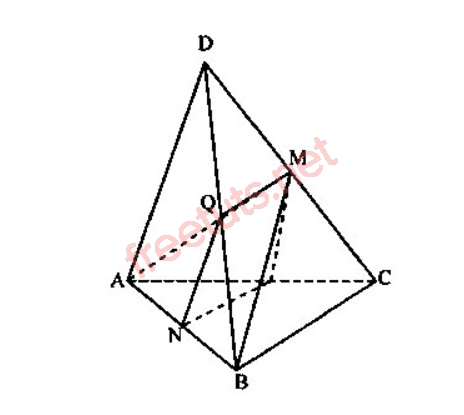
Gọi M là trung điểm CD, Q là trung điểm của DB, thời điểm này, tớ sở hữu AM vuông góc với CD, BM vuông góc với CD.
Theo đề bài bác, tớ có: góc AMB vì chưng 90 chừng.
Xét tam giác AMB tớ có:
AM = BM, góc AMB vì chưng 90 chừng, nên suy rời khỏi tam giac AMB vuông cân nặng bên trên M.
Suy ra:
Cạnh BM = (a√2)/2.
Vì M là trung điểm CD nên CD = 2CM = 2√(BC^2 - BM^2) = a√2
Vậy, thể tích tứ diện ABCD là:
V(ABC) = 1/3.CD.S(ABM) = 1/6.CD.AM.BM = (a^3√2)/12.
b. Gọi N, P.., Q theo thứ tự là trung điểm của 3 cạnh AB, AC và BD.
Ta có:
Góc tạo nên vì chưng hai tuyến đường chéo cánh AD và BC = góc tạo nên vì chưng 2 lối chéo cánh NP và MP.
Xét tam giác AMB vuông cân nặng bên trên M, nên suy ra:
MN = AB/2 = a/2 = NP = PM.
Xét tam giác MNP sở hữu MN = NP = PM, nên suy rời khỏi tam giác MNP là tam giác đều.
Vậy góc MPN = 60 chừng, nên Góc tạo nên vì chưng hai tuyến đường chéo cánh AD và BC = 60 chừng.
Bài 2: Cho tứ diện đều ABCD, Gọi (M) là hình chén bát diện đều phải sở hữu những đỉnh là trung điểm những cạnh của tứ diện đều ABCD. Tính tỉ số V(M)/V(ABCD)
Lời giải:
Gọi cạnh của tứ diện đều ABCD có tính nhiều năm vì chưng a, thì cạnh của chén bát diện đều (M) là a/2.
Lúc này tớ có
Xem thêm: học sinh trung học cơ sở Tiếng Anh là gì
V(ABCD) = a^3(√2/12), V(M) = 1/3.(a/2)^3√2 = (a^3√2)/24
Từ ê suy ra: V(H)/V(ABCD) = 1/2
Như vậy, qua chuyện nội dung bài viết bên trên, cuongthinhcorp.com.vn tiếp tục share cho những em cụ thể những công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3, 2a và một trong những bài bác tập dượt tương quan. Hy vọng phía trên được xem là những kỹ năng có ích mang đến chúng ta học viên trung học phổ thông. Chúc những em tiếp thu kiến thức đảm bảo chất lượng, đạt thành quả cao.